人教A版 (2019)选择性必修 第一册3.1 椭圆优秀学案

3.1.1　椭圆及其标准方程

【学习目标】

1．掌握椭圆的定义．

2．掌握椭圆标准方程的两种形式．

3．能根据条件确定椭圆的标准方程．

【学习过程】

一、课前预习

预习课本P105～109，思考并完成以下问题

1．平面内满足什么条件的点的轨迹为椭圆？椭圆的焦点、焦距分别是什么？

2．椭圆的标准方程是什么？

二、课前小测

1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)

(1)平面内到两定点距离之和等于定长的点的轨迹为椭圆(　　)

(2)已知椭圆的焦点是F1，F2，P是椭圆上的一动点，如果延长F1P到Q，使得|PQ|＝|PF2|，则动点Q的轨迹为圆(　　)

(3)方程＋＝1(a>0，b>0)表示的曲线是椭圆(　　)

2．若椭圆＋＝1的一个焦点坐标为(1,0)，则实数m的值为(　　)

A．1　　　　　　　　 B．2

C．4 D．6

3．设P是椭圆＋＝1上的点，若F1，F2是椭圆的两个焦点，则|PF1|＋|PF2|等于(　　)

A．4 B．5

C．8 D．10

4．若椭圆的焦距为6，a－b＝1，则椭圆的标准方程为________________．

三、新知探究

1．椭圆的定义

平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．

[说明]　定义中的条件2a>|F1F2|>0不能少，这是根据三角形中的两边之和大于第三边得出来的．否则：

①当2a＝|F1F2|时，其轨迹为线段F1F2；

②当2a<|F1F2|时，其轨迹不存在．

2．椭圆的标准方程

[说明]　椭圆的标准方程的特征

(1)几何特征：椭圆的中心在坐标原点，焦点在x轴或y轴上．

(2)代数特征：方程右边为1，左边是关于与的平方和，并且分母为不相等的正值.

四、题型突破

题型一　求椭圆的标准方程

[例1] 求适合下列条件的椭圆的标准方程．

(1)椭圆的两个焦点的坐标分别是(－4,0)，(4,0)，椭圆上一点P到两焦点距离的和等于10；

(2)椭圆的两个焦点的坐标分别是(0，－2)，(0,2)，并且椭圆经过点；

(3)椭圆的焦点在x轴上，a∶b＝2∶1，c＝.

反思感悟

确定椭圆的方程包括“定位”和“定量”两个方面

(1)“定位”是指确定与坐标系的相对位置，在中心为原点的前提下，确定焦点位于哪条坐标轴上，以判断方程的形式；

(2)“定量”是指确定a2，b2的具体数值，常根据条件列方程求解．

跟踪训练

1、求适合下列条件的椭圆的标准方程：

(1)经过两点(2，－)，；

(2)过点(，－)，且与椭圆＋＝1有相同的焦点．

题型二　椭圆的定义及其应用

[例2] (1)已知椭圆的方程为＋＝1(a>5)，它的两个焦点分别为F1，F2，且|F1F2|＝8，弦AB过点F1，则△ABF2的周长为(　　)

A．10　　　　　　　　  B．20

C．2 D．4

(2)如图所示，已知椭圆的方程为＋＝1，若点P在第二象限，且∠PF1F2＝120°，则△PF1F2的面积为________．

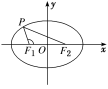
反思感悟

椭圆定义的应用技巧

(1)椭圆的定义具有双向作用，即若|MF1|＋|MF2|＝2a(2a>|F1F2|)，则点M的轨迹是椭圆；反之，椭圆上任意一点M到两焦点的距离之和必为2a.

(2)涉及焦点三角形面积时，可把|PF1|，|PF2|看作一个整体，运用|PF1|2＋|PF2|2＝(|PF1|＋|PF2|)2－2|PF1|·|PF2|及余弦定理求出|PF1|·|PF2|，而无需单独求解．

跟踪训练

2. 如图所示，已知椭圆的两焦点为F1(－1,0)，F2(1,0)，P为椭圆上一点，且2|F1F2|＝|PF1|＋|PF2|，则椭圆的标准方程为____________．

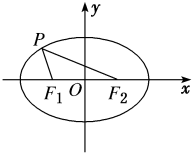
3. 已知椭圆＋＝1的左、右焦点分别为F1，F2，点P在椭圆上，若|PF1|＝4，则∠F1PF2＝________.

题型三　与椭圆有关的轨迹问题

[例3]　(1)已知P是椭圆＋＝1上一动点，O为坐标原点，则线段OP中点Q的轨迹方程为________．

(2)已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C，求C的方程．

反思感悟

解决与椭圆有关的轨迹问题的两种方法

(1)定义法

用定义法求椭圆方程的思路是：先观察、分析已知条件，看所求动点轨迹是否符合椭圆的定义．若符合椭圆的定义，则用待定系数法求解即可．

(2)相关点法

有些问题中的动点轨迹是由另一动点按照某种规律运动而形成的，只要把所求动点的坐标“转移”到另一个动点在运动中所遵循的条件中去，即可解决问题，这种方法称为相关点法．

跟踪训练

4.求过点P(3,0)且与圆x2＋6x＋y2－91＝0相内切的动圆圆心的轨迹方程．

五、达标检测

1．设F1，F2是椭圆E：＋＝1(a>b>0)的左、右焦点，P为直线x＝上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为(　　)

A.　　　　B.　　　　C.　　　　D.

2．椭圆C：＋＝1的左、右顶点分别为A1，A2，点P在C上且直线PA2斜率的取值范围是[－2，－1]，那么直线PA1斜率的取值范围是(　　)

A.   B.

C.   D.

3．(福建)设P，Q分别为圆x2＋(y－6)2＝2和椭圆＋y2＝1上的点，则P，Q两点间的最大距离是(　　)

A．5   B.＋ 

C．7＋   D．6

4．(辽宁)已知椭圆C：＋＝1(a>b>0)的左焦点为F，C与过原点的直线相交于A，B两点，连接AF，BF.若|AB|＝10，|AF|＝6，cos∠ABF＝，则C的离心率e＝________.

六、本课小结

1．对椭圆定义的两点说明

(1)前提：椭圆定义是解决椭圆问题的常用工具，定义中“平面内”这一条件不能丢掉，否则动点的轨迹就是空间图形椭球体的表面．

(2)限制条件：椭圆中到两定点的距离之和记为2a，只有2a大于两定点间的距离|F1F2|时，动点的轨迹才是椭圆，在判断一曲线是否为椭圆时，一定不要忽略此限制条件．

2．对椭圆标准方程的三点认识

(1)标准方程的几何特征：椭圆的中心在坐标原点，焦点在x轴或y轴上，对称轴是坐标轴．

(2)标准方程的代数特征：方程右边为1，左边是关于与的平方和，并且分母为不相等的正值，当椭圆的焦点在x轴上时，含x项的分母大；当椭圆的焦点在y轴上时，含y项的分母大，已知椭圆的方程解题时，应特别注意a>b>0这个条件．

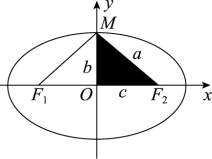
(3)a，b，c三个量的关系：椭圆的标准方程中，a表示椭圆上的点M到两焦点间距离的和的一半，可借助图形帮助记忆．a，b，c(都是正数)恰是构成一个直角三角形的三条边，a是斜边，所以a>b，a>c，且a2＝b2＋c2(如图所示)．

参考答案

课前小测

1．答案：(1)×　(2)√　(3)×

2．答案：C

3．答案：D

4．答案：＋＝1或＋＝1

题型突破

[例1] [解]　(1)椭圆的焦点在x轴上，故设椭圆的标准方程为＋＝1(a>b>0)．

∵2a＝10，c＝4，∴b2＝a2－c2＝9.

∴椭圆的标准方程为＋＝1.

(2)椭圆的焦点在y轴上，故设椭圆的标准方程为＋＝1(a>b>0)．

由椭圆的定义，知2a＝＋

＝＋＝2，

∴a＝.

又∵c＝2，∴b2＝a2－c2＝10－4＝6.

∴椭圆的标准方程为＋＝1.

(3)∵c＝，∴a2－b2＝c2＝6.①

又由a∶b＝2∶1，得a＝2b，代入①得4b2－b2＝6，

∴b2＝2，∴a2＝8.

又∵椭圆的焦点在x轴上，

∴椭圆的标准方程为＋＝1.

跟踪训练

1. 解： (1)法一：(分类讨论法)若焦点在x轴上，设椭圆的标准方程为＋＝1(a>b>0)．

由已知条件得解得

所以所求椭圆的标准方程为＋＝1.

若焦点在y轴上，设椭圆的标准方程为＋＝1(a>b>0)．

由已知条件得解得

则a2<b2，与题设中a>b>0矛盾，舍去．

综上，所求椭圆的标准方程为＋＝1.

法二：(待定系数法)设椭圆的一般方程为Ax2＋By2＝1(A>0，B>0，A≠B)．将两点(2，－)，代入，得解得

所以所求椭圆的标准方程为＋＝1.

(2)因为所求椭圆与椭圆＋＝1的焦点相同，所以其焦点在y轴上，且c2＝25－9＝16.设它的标准方程为＋＝1(a>b>0)．

因为c2＝16，且c2＝a2－b2，故a2－b2＝16.①

又点(，－)在椭圆上，所以＋＝1，

即＋＝1.②

由①②得b2＝4，a2＝20，所以所求椭圆的标准方程为

＋＝1.

[例2]　[解析]　(1)∵a>5，∴椭圆的焦点在x轴上．又c＝4，

∴a2－25＝42，∴a＝.由椭圆的定义知△ABF2的周长＝|BA|＋|F2B|＋|F2A|＝|BF1|＋|BF2|＋|AF1|＋|AF2|＝4a＝4.

(2)由已知得a＝2，b＝，

所以c＝＝＝1，|F1F2|＝2c＝2.

在△PF1F2中，由余弦定理，得

|PF2|2＝|PF1|2＋|F1F2|2－2|PF1|·|F1F2|·cos 120°，

即|PF2|2＝|PF1|2＋4＋2|PF1|.①

由椭圆定义，得|PF1|＋|PF2|＝4，

即|PF2|＝4－|PF1|.②

将②代入①解得|PF1|＝.

所以S△PF1F2＝|PF1|·|F1F2|·sin 120°

＝××2×＝，

即△PF1F2的面积是.

[答案]　(1)D　(2)

跟踪训练

2. 解析：设椭圆的标准方程为＋＝1(a>b>0)，焦距为2c，则由已知得c＝1，|F1F2|＝2，所以4＝|PF1|＋|PF2|＝2a，所以a＝2，所以b2＝a2－c2＝4－1＝3，所以椭圆的标准方程为＋＝1.

答案：＋＝1

3. 解析：由题意，得a2＝9，∴a＝3，c2＝a2－b2＝9－2＝7，∴c＝，∴|F1F2|＝2.

∵|PF1|＝4，∴|PF2|＝2a－|PF1|＝2.

∴cos∠F1PF2＝＝＝－，

∴∠F1PF2＝120°.

答案：120°

[例3] [解析]　(1)设P(xP，yP)，Q(x，y)，

由中点坐标公式得所以

又点P在椭圆＋＝1上，所以＋＝1，

即x2＋＝1.

答案：x2＋＝1

(2)解：由已知得圆M的圆心为M(－1,0)，半径r1＝1；圆N的圆心为N(1,0)，半径r2＝3.设圆P的圆心为P(x，y)，半径为R.动圆P与圆M外切并且与圆N内切，

所以|PM|＋|PN|＝(R＋r1)＋(r2－R)＝r1＋r2＝4.

由椭圆定义可知，曲线C是以M，N为左、右焦点，长半轴长为2，短半轴长为的椭圆(左顶点除外)，其方程为＋＝1(x≠－2)．

跟踪训练

4. 解：圆方程配方整理得(x＋3)2＋y2＝102，圆心为C1(－3，0)，半径为R＝10.设所求动圆圆心为C(x，y)，半径为r，依题意有消去r得R－|PC|＝|CC1|⇒|PC|＋|CC1|＝R，即|PC|＋|CC1|＝10.

又P(3,0)，C1(－3,0)，且|PC1|＝6<10.可见C点是以P，C1为两焦点的椭圆，且c＝3,2a＝10，

所以a＝5，从而b＝4，

故所求的动圆圆心的轨迹方程为＋＝1.

五、达标检测

1．答案：C

解析：设直线x＝与x轴交于点M，则∠PF2M＝60°，

在Rt△PF2M中，PF2＝F1F2＝2c，F2M＝－c，

故cos 60°＝＝＝，解得＝，故离心率e＝.

2．答案：B

解析：由题意知点P在第一象限，设点P横坐标为x，则纵坐标为y＝×，

由PA2的斜率得：1≤×≤2，即≤≤，

PA1的斜率为×，所以PA1的斜率取值范围为.

故选B.

3．答案：D

解析：将两个动点间的距离转化为一个动点和一个定点间的距离．

设Q(m，n)(－1≤n≤1)，因为圆心C(0,6)，故|QC|＝　①，

因为＋n2＝1　②，联立①②，|QC|＝，

因为－1≤n≤1，故当n＝－时，|QC|有最大值，最大值为5，

所以|PQ|max＝|QC|max＋＝6，

故选D.

4. 答案：

解析：由余弦定理得AF2＝AB2＋BF2－2AB·BF·cos∠ABF，

即36＝100＋BF2－2×10·BF·，化简得BF2－16BF＋64＝0，解得BF＝8.

∴△ABF为直角三角形．c＝AB＝5，

设右焦点为F2，连接AF2，BF2，由对称性可知四边形AFBF2为矩形．

∴AF2＝8，由椭圆定义2a＝14，∴a＝7，∴离心率e＝.