【同步导学案】高中数学人教A版(2019)选修第一册-- 2.2.1直线的点斜式方程 导学案（有答案）

这是一份【同步导学案】高中数学人教A版(2019)选修第一册-- 2.2.1直线的点斜式方程 导学案（有答案），共6页。学案主要包含了学习目标，学习过程等内容，欢迎下载使用。
2.2.1　直线的点斜式方程【学习目标】1.理解直线的倾斜角和斜率的概念．2.掌握求直线斜率的两种方法．3.了解在平面直角坐标系中确定一条直线的几何要素.【学习过程】一、课前预习预习课本P59～61，思考并完成以下问题1．确定直线的几何要素是什么？ 2．直线的点斜式方程是怎样推导的？ 3．直线的点斜式方程与斜截式方程的结构形式分别是什么？ 4．直线的纵截距是怎样定义的？二、课前小测1．直线的点斜式方程y－y0＝k(x－x0)可以表示(　　)A．任何一条直线　　　　 B．不过原点的直线C．不与坐标轴垂直的直线  D．不与x轴垂直的直线2．下面四个直线方程中，可以看作是直线的斜截式方程的是(　　)A．x＝3   B．2x＋y－1＝0C．2y＝x  D．y＝4x－13．已知直线l的点斜式方程为y－1＝x－1，那么直线l的斜率为________，倾斜角为________，在y轴上的截距为________．三、新知探究一、直线的点斜式方程和斜截式方程名称点斜式斜截式已知条件点P(x0，y0)和斜率k斜率k和直线在y轴上的截距b图示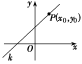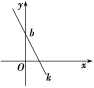方程y－y0＝k(x－x0)y＝kx＋b适用范围斜率存在 二、直线l在y轴上的截距定义：直线l与y轴交点(0，b)的纵坐标b叫作直线l在y轴上的截距． 四、题型突破题型一 求直线的点斜式方程[例1]　(1)经过点(－5,2)且平行于y轴的直线方程为________．(2)直线y＝x＋1绕着其上一点P(3,4)逆时针旋转90°后得直线l，则直线l的点斜式方程为________．(3)求过点P(1,2)且与直线y＝2x＋1平行的直线方程为________．     反思感悟求直线的点斜式方程的方法步骤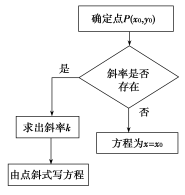： 跟踪训练1．已知点A(3,3)和直线l：y＝x－.求：(1)过点A且与直线l平行的直线的点斜式方程；(2)过点A且与直线l垂直的直线的点斜式方程．      题型二　求直线的斜截式方程[例2]　根据条件写出下列直线的斜截式方程：(1)斜率为2，在y轴上的截距是5；(2)倾斜角为150°，在y轴上的截距是－2；(3)经过点(3,4)且在两坐标轴上的截距相等．    解题策略直线的斜截式方程的求解策略(1)用斜截式求直线方程，只要确定直线的斜率和截距即可，同时要特别注意截距和距离的区别．(2)直线的斜截式方程y＝kx＋b不仅形式简单，而且特点明显，k是直线的斜率，b是直线在y轴上的截距，只要确定了k和b的值，直线的图象就一目了然．因此，在解决直线的图象问题时，常通过把直线方程化为斜截式方程，利用k，b的几何意义进行判断． 跟踪训练2．已知直线l1的方程为y＝－2x＋3，l2的方程为y＝4x－2，直线l与l1平行且与l2在y轴上的截距相同，求直线l的方程．      题型三　利用直线的斜截式方程判断两直线位置关系[例3]　(1)当a为何值时，直线l1：y＝－x＋2a与直线l2：y＝(a2－2)x＋2平行？(2)当a为何值时，直线l1：y＝(2a－1)x＋3与直线l2：y＝4x－3垂直？      易错提醒对于不能用斜截式方程表示的直线，判断它们的位置关系时，需注意：(1)若两条直线的斜率均不存在，则有l1∥l2或l1与l2重合．(2)若一条直线的斜率不存在，另一条直线的斜率为0，则有l1⊥l2.(3)若一条直线的斜率不存在，另一条直线的斜率存在但不为0，则两条直线既不平行也不垂直． 跟踪训练3．已知直线y＝ax－2和y＝(a＋2)x＋1互相垂直，则a＝________. 4．若直线l1：y＝－x－与直线l2：y＝3x－1互相平行，则a＝________. 五、达标检测1．直线y－b＝2(x－a)在y轴上的截距为(　　)A．a＋b　  B．2a－b　　C．b－2a　　D．|2a－b|2．已知直线l过点(0,7)，且与直线y＝－4x＋2平行，则直线l的方程为(　　)A．y＝－4x－7  B．y＝4x－7C．y＝4x＋7  D．y＝－4x＋73．直线y＝k(x－2)＋3必过定点，该定点坐标是________． 六、本课小结1．建立点斜式方程的依据是：直线上任一点与这条直线上一个定点的连线的斜率相同，故有＝k，此式是不含点P1(x1，y1)的两条反向射线的方程，必须化为y－y1＝k(x－x1)才是整条直线的方程．当直线的斜率不存在时，不能用点斜式表示，此时方程为x＝x1.2．斜截式方程可看作点斜式的特殊情况，表示过(0，b)点、斜率为k的直线y－b＝k(x－0)，即y＝kx＋b，其特征是方程等号的一端只是一个y，其系数是1；等号的另一端是x的一次式，而不一定是x的一次函数．如y＝c是直线的斜截式方程，而2y＝3x＋4不是直线的斜截式方程．
参考答案课前小测1．答案：D2．答案：D3．答案：1　45°　0 题型突破[例1] 解析：(1)∵直线平行于y轴，∴直线不存在斜率，∴方程为x＝－5.(2)直线y＝x＋1的斜率k＝1，所以倾斜角为45°.由题意知，直线l的倾斜角为135°，所以直线l的斜率k′＝tan 135°＝－1，又点P(3,4)在直线l上，由点斜式方程知，直线l的方程为y－4＝－(x－3)．(3)由题意知，所求直线的斜率为2，且过点P(1,2)，∴直线方程为y－2＝2(x－1)，即2x－y＝0.答案：(1)x＝－5　(2)y－4＝－(x－3)　(3)2x－y＝0 跟踪训练1．解析：因为直线l：y＝x－，所以该直线的斜率k＝.(1)过点A(3,3)且与直线l平行的直线方程为y－3＝(x－3)．(2)过点A(3,3)且与直线l垂直的直线方程为y－3＝－(x－3)． [例2]　解析：(1)由直线方程的斜截式可知，所求直线的斜截式方程为y＝2x＋5.(2)∵倾斜角为150°，∴斜率k＝tan 150°＝－.由斜截式可得方程为y＝－x－2.(3)设直线在两坐标轴上的截距为a，当a＝0时，直线的斜截式方程为y＝x.当a≠0时，设直线的斜截式方程为y＝－x＋b，则有4＝－3＋b，即b＝7.此时方程为y＝－x＋7.故所求直线方程为y＝x或y＝－x＋7. 跟踪训练2．解析：由斜截式方程知直线l1的斜率k1＝－2，又∵l∥l1，∴l的斜率k＝k1＝－2.由题意知l2在y轴上的截距为－2，∴l在y轴上的截距b＝－2，由斜截式可得直线l的方程为y＝－2x－2. [例3] 解析：(1)由题意可知，kl1＝－1，kl2＝a2－2，∵l1∥l2，∴解得a＝－1.故当a＝－1时，直线l1：y＝－x＋2a与直线l2：y＝(a2－2)x＋2平行．(2)由题意可知，kl1＝2a－1，kl2＝4，∵l1⊥l2，∴4(2a－1)＝－1，解得a＝.故当a＝时，直线l1：y＝(2a－1)x＋3与直线l2：y＝4x－3垂直．跟踪训练3．解析：由题意可知a·(a＋2)＝－1，解得a＝－1.答案：－14．解析：由题意可知解得a＝－.答案：－ 达标检测1．解析：令x＝0，得y＝b－2a.答案：C2．解析：过点(0,7)且与直线y＝－4x＋2平行的直线方程为y－7＝－4x，即直线l的方程为y＝－4x＋7，故应选D.答案：D3．解析：将直线方程化为点斜式得y－3＝k(x－2)，∴过定点(2,3)．答案：(2,3)