

北京市昌平区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类
展开北京市昌平区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类
一.实数的运算(共2小题)
1.(2020秋•昌平区期末)计算:tan60°+cos245°﹣sin30°.
2.(2022秋•昌平区期末)计算:tan30°+2cos45°﹣sin260°.
二.反比例函数与一次函数的交点问题(共1小题)
3.(2021秋•昌平区期末)如图,在平面直角坐标系xOy中,A(a,2)是一次函数y=x﹣1的图象与反比例函数y=(k≠0)的图象的交点.
(1)求反比例函数y=(k≠0)的表达式;
(2)过点P(n,0)且垂直于x轴的直线与一次函数图象,反比例函数图象的交点分别为M,N,当S△OPM>S△OPN时,直接写出n的取值范围.
三.二次函数图象与系数的关系(共2小题)
4.(2020秋•昌平区期末)在平面直角坐标系xOy中,抛物线y=ax2+bx+3与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)①直接写出抛物线的对称轴是 ;
②用含a的代数式表示b;
(2)横、纵坐标都是整数的点叫做整点.若抛物线与x轴交于P、Q两点,该抛物线在P、Q之间的部分与线段PQ所围成的区域(不包括边界)恰有七个整点,结合函数图象,求a的取值范围.
5.(2021秋•昌平区期末)在平面直角坐标系xOy中,点(1,m)和点(3,n)在二次函数y=x2+bx的图象上.
(1)当m=﹣3时.
①求这个二次函数的顶点坐标;
②若点(﹣1,y1),(a,y2)在二次函数的图象上,且y2>y1,则a的取值范围是 ;
(2)当mn<0时,求b的取值范围.
四.圆周角定理(共1小题)
6.(2022秋•昌平区期末)我们在课上证明圆周角定理时,需要讨论圆心与圆周角的三种不同位置分别证明,下面给出了情形(1)的证明过程,请你在情形(2)和情形(3)中选择其一证明即可.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
已知:如图,在⊙O中,弧AB所对的圆周角是∠ACB,圆心角是∠AOB.
求证:∠ACB=∠AOB.
情形(1)
证明:如图(1),当圆心O在∠ACB的边上时,
∵OC=OB,
∴∠C=∠B.
∵∠AOB是△OBC中∠COB的外角,
∴∠AOB=∠C+∠B.
∴∠AOB=2∠C.
即∠C=∠AOB.
请你选择情形(2)或情形(3),并证明.
五.切线的判定与性质(共1小题)
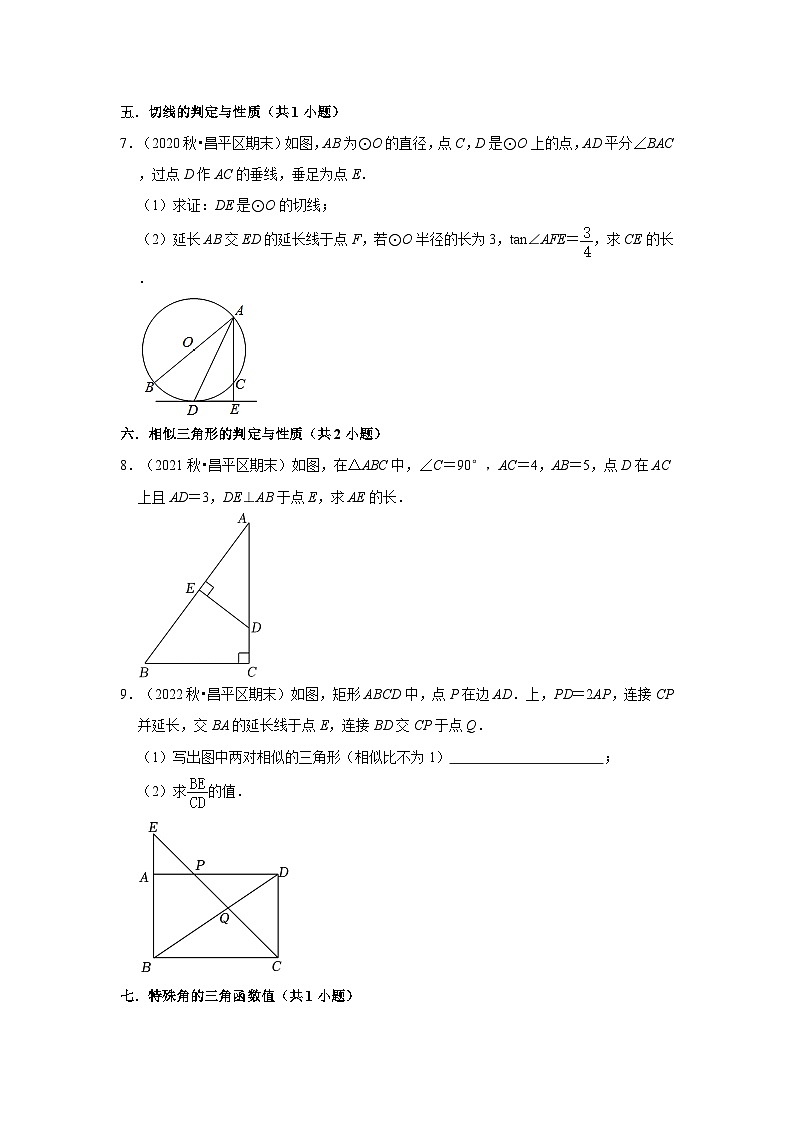
7.(2020秋•昌平区期末)如图,AB为⊙O的直径,点C,D是⊙O上的点,AD平分∠BAC,过点D作AC的垂线,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)延长AB交ED的延长线于点F,若⊙O半径的长为3,tan∠AFE=,求CE的长.
六.相似三角形的判定与性质(共2小题)
8.(2021秋•昌平区期末)如图,在△ABC中,∠C=90°,AC=4,AB=5,点D在AC上且AD=3,DE⊥AB于点E,求AE的长.
9.(2022秋•昌平区期末)如图,矩形ABCD中,点P在边AD.上,PD=2AP,连接CP并延长,交BA的延长线于点E,连接BD交CP于点Q.
(1)写出图中两对相似的三角形(相似比不为1) ;
(2)求的值.
七.特殊角的三角函数值(共1小题)
10.(2021秋•昌平区期末)计算:2sin60°+tan45°﹣cos30°tan60°.
八.解直角三角形(共1小题)
11.(2021秋•昌平区期末)如图,在△ABC中,∠B=30°,AB=4,AD⊥BC于点D且tan∠CAD=,求BC的长.
九.解直角三角形的应用(共1小题)
12.(2021秋•昌平区期末)居庸关位于距北京市区50余公里外的昌平区境内,是京北长城沿线上的著名古关城,有“天下第一雄关”的美誉.某校数学社团的同学们使用皮尺和测角仪等工具,测量南关主城门上城楼顶端距地面的高度,下表是小强填写的实践活动报告的部分内容:请你帮他计算出城楼的高度AD.(结果精确到0.1m,sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
题目
测量城楼顶端到地面的高度
测量目标
示意图
相关数据
BM=1.6m,BC=13m,∠ABC=35°,∠ACE=45°
北京市昌平区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类
参考答案与试题解析
一.实数的运算(共2小题)
1.(2020秋•昌平区期末)计算:tan60°+cos245°﹣sin30°.
【答案】见试题解答内容
【解答】解:tan60°+cos245°﹣sin30°
=×+﹣
=3+﹣
=3.
2.(2022秋•昌平区期末)计算:tan30°+2cos45°﹣sin260°.
【答案】+.
【解答】解:原式=×+2×﹣()2
=1+﹣
=+.
二.反比例函数与一次函数的交点问题(共1小题)
3.(2021秋•昌平区期末)如图,在平面直角坐标系xOy中,A(a,2)是一次函数y=x﹣1的图象与反比例函数y=(k≠0)的图象的交点.
(1)求反比例函数y=(k≠0)的表达式;
(2)过点P(n,0)且垂直于x轴的直线与一次函数图象,反比例函数图象的交点分别为M,N,当S△OPM>S△OPN时,直接写出n的取值范围.
【答案】(1);
(2)n<﹣2或n>3.
【解答】解:(1)把A(a,2)代入y=x﹣1,
得,a﹣1=2,解得a=3,
∴点A坐标为(3,2).
把A(3,2)代入,
得,2=,解得k=6.
所以反比例函数表达式为.;
(2)一次函数y=x﹣1的图象与的图象相交于点(3,2)和(﹣2,﹣3).
观察函数图象可知:过点P(n,0)且垂直于x轴的直线与一次函数图象,反比例函数图象的交点分别为M,N,当S△OPM>S△OPN时,PM>PN,
则n的取值范围是n<﹣2或n>3.
三.二次函数图象与系数的关系(共2小题)
4.(2020秋•昌平区期末)在平面直角坐标系xOy中,抛物线y=ax2+bx+3与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)①直接写出抛物线的对称轴是 直线x=1 ;
②用含a的代数式表示b;
(2)横、纵坐标都是整数的点叫做整点.若抛物线与x轴交于P、Q两点,该抛物线在P、Q之间的部分与线段PQ所围成的区域(不包括边界)恰有七个整点,结合函数图象,求a的取值范围.
【答案】(1)①直线x=1;②b=﹣2a.
(2)10<a≤11 或﹣1≤a≤.
【解答】解:(1)①∵A与B关于对称轴x=1对称,
∴抛物线对称轴为直线x=1,
故答案为直线x=1;
②∵抛物线y=ax2+bx+c与y轴交于点A,
∴A(0,c),
点A向右平移2个单位长度,得到点B(2,c),
∵点B在抛物线上,
∴4a+2b+c=c,
∴b=﹣2a.
(2)由题可知:A(0,3)B(2,3),
①若a>0时,如图1,在P、Q之间的部分与线段PQ所围成的区域(不包括边界)内的七个整点为(1,﹣1),(1,﹣2),(1,﹣3),(1,﹣4),(1,﹣5),(1,﹣6),(1,﹣7),
∵x=1时,y=a+b+3=﹣a+3,
∴顶点为(1,﹣a+3),
∴﹣8≤﹣a+3<﹣7,
∴10<a≤11;
②若a<0时,如图2,在P、Q之间的部分与线段PQ所围成的区域(不包括边界)内的七个整点为(0,1),(0,2),(2,1),(2,2),(1,1),(1,2),(1,3),
当x=﹣1时,y=3a+3,
∵恰有7个整数点
∴,
∴﹣1≤a≤,
综上,a的取值范围是10<a≤11 或﹣1≤a≤.
5.(2021秋•昌平区期末)在平面直角坐标系xOy中,点(1,m)和点(3,n)在二次函数y=x2+bx的图象上.
(1)当m=﹣3时.
①求这个二次函数的顶点坐标;
②若点(﹣1,y1),(a,y2)在二次函数的图象上,且y2>y1,则a的取值范围是 a<﹣1或a>5 ;
(2)当mn<0时,求b的取值范围.
【答案】(1)(2,﹣4);
(2)a<﹣1或a>5;
(3)﹣3<b<﹣1.
【解答】解:(1)当m=﹣3时.
①把点(1,﹣3)代入y=x2+bx,得b=﹣4,
二次函数表达式为y=x2﹣4x=(x﹣2)2﹣4,
所以顶点坐标为(2,﹣4);
②∵抛物线y=x2﹣4x=(x﹣2)2﹣4.
∴开口向上,对称轴为直线x=2,
∴点(﹣1,y1)关于直线x=2的对称点为(5,y1),
∵点(﹣1,y1),(a,y2)在二次函数的图象上,且y2>y1,
∴a<﹣1或a>5,
故答案为:a<﹣1或a>5;
(2)将点(1,m),(3,n)代入y=x2+bx,可得m=1+b,n=9+3b.
当mn<0时,有两种情况:
①若把m=1+b,n=9+3b代入可得此时不等式组无解.
②若把m=1+b,n=9+3b代入可得解得﹣3<b<﹣1.
所以﹣3<b<﹣1.
四.圆周角定理(共1小题)
6.(2022秋•昌平区期末)我们在课上证明圆周角定理时,需要讨论圆心与圆周角的三种不同位置分别证明,下面给出了情形(1)的证明过程,请你在情形(2)和情形(3)中选择其一证明即可.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
已知:如图,在⊙O中,弧AB所对的圆周角是∠ACB,圆心角是∠AOB.
求证:∠ACB=∠AOB.
情形(1)
证明:如图(1),当圆心O在∠ACB的边上时,
∵OC=OB,
∴∠C=∠B.
∵∠AOB是△OBC中∠COB的外角,
∴∠AOB=∠C+∠B.
∴∠AOB=2∠C.
即∠C=∠AOB.
请你选择情形(2)或情形(3),并证明.
【答案】证明过程见解答.
【解答】证明:如图(2):连接CO并延长交⊙O于点D,
∵OA=OC,
∴∠A=∠ACO,
∵∠AOD=∠A+∠ACO,
∴∠AOD=2∠ACO,
∵OB=OC,
∴∠B=∠OCB,
∵∠BOD=∠B+∠OCB,
∴∠BOD=2∠OCB,
∴∠AOB=∠AOD+∠BOD
=2∠ACO+2∠OCB
=2∠ACB;
∴∠ACB=∠AOB,
如图(3):连接CO并延长交⊙O于点E,
∵OA=OC,
∴∠A=∠ACO,
∵∠AOE=∠A+∠ACO,
∴∠AOE=2∠ACO,
∵OB=OC,
∴∠B=∠OCB,
∵∠BOE=∠B+∠OCB,
∴∠BOE=2∠OCB,
∴∠AOB=∠BOE﹣AOE
=2∠OCB﹣2∠ACO
=2∠ACB;
∴∠ACB=∠AOB.
五.切线的判定与性质(共1小题)
7.(2020秋•昌平区期末)如图,AB为⊙O的直径,点C,D是⊙O上的点,AD平分∠BAC,过点D作AC的垂线,垂足为点E.
(1)求证:DE是⊙O的切线;
(2)延长AB交ED的延长线于点F,若⊙O半径的长为3,tan∠AFE=,求CE的长.
【答案】见试题解答内容
【解答】(1)证明:连接OD.
∵AD平分∠BAC,
∴∠OAD=∠DAE,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠DAE,
∴OD∥AE,
∵AC⊥DE,
∴OD⊥DE,
∵OD是⊙O半径,
∴DE是⊙O的切线.
(2)解:连接BC,交OD于点M.
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠AED=∠ODE=90°,
∴∠ACB=∠AED=∠ODE=90°,
∴四边形CEDM是矩形,
∴CE=MD,CM∥DE,
∴∠F=∠ABC,
在Rt△OBM中,OB=3,tan∠ABC=,
设OM=3x,BM=4x,
∴(3x)2+(4x)2=32,
解得x=,负值舍去,
∴OM=
∴CE=MD=3﹣=.
六.相似三角形的判定与性质(共2小题)
8.(2021秋•昌平区期末)如图,在△ABC中,∠C=90°,AC=4,AB=5,点D在AC上且AD=3,DE⊥AB于点E,求AE的长.
【答案】.
【解答】解:∵DE⊥AB于点E,∠C=90°,
∴∠AED=∠C=90°,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,
∵AB=5,AD=3,AC=4,
∴,
∴AE=.
9.(2022秋•昌平区期末)如图,矩形ABCD中,点P在边AD.上,PD=2AP,连接CP并延长,交BA的延长线于点E,连接BD交CP于点Q.
(1)写出图中两对相似的三角形(相似比不为1) △EAP∽△EBC,△EBQ∽△CDQ ;
(2)求的值.
【答案】(1)△EAP∽△EBC,△EBQ∽△CDQ;
(2)=.
【解答】解:(1)∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC,
∴△EAP∽△EBC,△EBQ∽△CDQ;
故答案为:△EAP∽△EBC,△EBQ∽△CDQ(答案不唯一);
(2)∵△EAP∽△EBC,
∴=,
∵PD=2AP,AD=BC,
∴==,
∵AB=CD,
∴==,
∴=.
七.特殊角的三角函数值(共1小题)
10.(2021秋•昌平区期末)计算:2sin60°+tan45°﹣cos30°tan60°.
【答案】.
【解答】解:2sin60°+tan45°﹣cos30°tan60°
=
=+1﹣
=.
八.解直角三角形(共1小题)
11.(2021秋•昌平区期末)如图,在△ABC中,∠B=30°,AB=4,AD⊥BC于点D且tan∠CAD=,求BC的长.
【答案】2+1.
【解答】解:∵AD⊥BC于点D,
∴△ABD,△ADC为直角三角形.
∵Rt△ADB中,∠B=30°,AB=4,
∴AD=2,BD=.
∵Rt△ADC中,tan∠CAD=,AD=2,
∴tan∠CAD=.
∴CD=1.
∴BC=+1.
九.解直角三角形的应用(共1小题)
12.(2021秋•昌平区期末)居庸关位于距北京市区50余公里外的昌平区境内,是京北长城沿线上的著名古关城,有“天下第一雄关”的美誉.某校数学社团的同学们使用皮尺和测角仪等工具,测量南关主城门上城楼顶端距地面的高度,下表是小强填写的实践活动报告的部分内容:请你帮他计算出城楼的高度AD.(结果精确到0.1m,sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
题目
测量城楼顶端到地面的高度
测量目标
示意图
相关数据
BM=1.6m,BC=13m,∠ABC=35°,∠ACE=45°
【答案】31.9.
【解答】解:根据题意,得BM=ED=1.6m,∠AEC=90°,
设AE为x m,在Rt△ACE中,
∵∠ACE=45°,
∴∠CAE=45°,
∴AE=CE,
在Rt△ABE中,
∵tan∠ABE=,
又∵∠ABE=35°,
∴tan35°=,
解得x≈30.3,
∴AD=AE+ED≈30.3+1.6≈31.9(m),
答:城楼顶端距地面约为31.9m.
北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类: 这是一份北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类,共13页。试卷主要包含了解方程,x+6+2k=0,已知抛物线y=﹣x2+x,已知二次函数y=x2+4x+3,已知二次函数y=x2﹣2x﹣3,之间关系的图象如图所示等内容,欢迎下载使用。
北京市通州区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类: 这是一份北京市通州区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类,共28页。试卷主要包含了0﹣+|2﹣|,,与y轴交于点C,的图象上,有这样一个问题,两点,求这个二次函数的解析式等内容,欢迎下载使用。
北京市密云区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类: 这是一份北京市密云区三年(2020-2022)九年级上学期期末数学试题汇编-03解答题(基础题)知识点分类,共25页。试卷主要包含了计算,0﹣2cs45°+|﹣4|,是该函数图象上的一个动点,已知二次函数y=x2﹣4x+3,已知二次函数y=x2﹣2x﹣3等内容,欢迎下载使用。












