

人教版2023年九年级上册第22章《二次函数》单元检测卷
展开人教版2023年九年级上册第22章《二次函数》单元检测卷
一、选择题(共30分)
1.下列函数是二次函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.二次函数![]() 的图象的顶点坐标是( )
的图象的顶点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知抛物线![]() 经过A
经过A![]() ,B
,B![]() 两点,则它的对称轴是( )
两点,则它的对称轴是( )
A.直线![]() B.直线
B.直线![]() C.直线
C.直线![]() D.无法确定
D.无法确定
4.若将抛物线![]() 向右平移3个单位,再向上平移2个单位,则所得抛物线解析式为( )
向右平移3个单位,再向上平移2个单位,则所得抛物线解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.一次函数![]() 与二次函数
与二次函数![]() 在同一坐标系内的图象可能为( )
在同一坐标系内的图象可能为( )
A.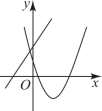 B.
B.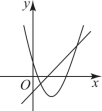
C.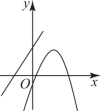 D.
D.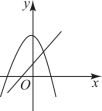
6.已知二次函数![]() ,当
,当![]() 时,则x的取值范围为( )
时,则x的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
7.已知函数![]() 图象上有三点
图象上有三点![]() 、
、![]() 、
、![]() ,试确定
,试确定![]() 、
、![]() 、
、![]() 的大小( )
的大小( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.小凯在画一个开口向上的二次函数图象时,列出如下表格:发现有一对对应值计算有误,则错误的那一对对应值所对的坐标是( )
x | … |
| 0 | 1 | 2 | … |
y | … |
| 4 |
| 2 | … |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱![]() 的高度为( )米.
的高度为( )米.
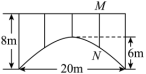
A.![]() 米 B.3米 C.
米 B.3米 C.![]() 米 D.4米
米 D.4米
10.在平面直角坐标系中,已知二次函数![]() 的图象如图所示,以下6个结论:
的图象如图所示,以下6个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤当
;⑤当![]() 时,二次函数有最大值;⑥当
时,二次函数有最大值;⑥当![]() 时,函数y的值随x的增大而减小;其中正确的序号有( )
时,函数y的值随x的增大而减小;其中正确的序号有( )
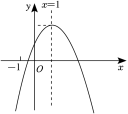
A.①②④ B.②③⑤ C.④⑤⑥ D.②④⑤
二、填空题(共28分)
11.如果函数![]() 是二次函数,则m的值为 .
是二次函数,则m的值为 .
12.抛物线![]() 的开口方向 .(“向上”或“向下”)
的开口方向 .(“向上”或“向下”)
13.已知抛物线![]() 与x轴有且只有一个交点,则
与x轴有且只有一个交点,则![]() .
.
14.在平面直角坐标系![]() 中,已知点
中,已知点![]() 是抛物线
是抛物线![]() 上任意一点,则
上任意一点,则![]() 长的最小值为 .
长的最小值为 .
15.某化工厂![]() 月份生产某种产品
月份生产某种产品![]() ,
,![]() 月份生产这种产品
月份生产这种产品![]() ,则
,则![]() 与产品产量的月平均增长率
与产品产量的月平均增长率![]() 之间的函数关系式是 .
之间的函数关系式是 .
16.已知二次函数![]() ,当
,当![]() 时,
时,![]() 的取值范围为 .
的取值范围为 .
17.已知一条抛物线的形状与抛物线![]() 形状相同,与另一条抛物线
形状相同,与另一条抛物线![]() 的顶点坐标相同,这条抛物线的表达式为 .
的顶点坐标相同,这条抛物线的表达式为 .
三、解答题(共62分)
18.(8分)根据下列条件,分别求出二次函数的解析式.
(1)已知图象的顶点坐标为(﹣1,﹣8),且过点(0,﹣6);
(2)已知图象经过点A(﹣1,0)、B(0,3),且对称轴为直线x=1.
19.(10分)二次函数 ![]()
![]() 的自变量x与对应的函数y的值(部分)如表所示:
的自变量x与对应的函数y的值(部分)如表所示:
x | … |
|
|
| 0 | 1 | 2 | … |
y | … | m | 7 | 1 |
| 1 | 7 | … |
解答下列问题:
(1)求这个二次函数的解析式;
(2)表格中m的值等于 ;
(3)在直角坐标系中,画出这个函数的图象.

20.(10分)如图,抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与y轴交于点C,连接
,与y轴交于点C,连接![]() ,与抛物线的对称轴交于点E,顶点为点D.
,与抛物线的对称轴交于点E,顶点为点D.
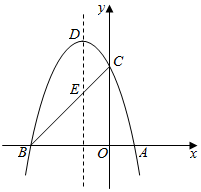
(1)求抛物线的解析式;
(2)求![]() 的面积.
的面积.
21.(10分)在平面直角坐标系中,当![]() 和
和![]() 时,二次函数
时,二次函数![]() (a,b是常数,a≠0)的函数值相等.
(a,b是常数,a≠0)的函数值相等.
(1)若该函数的最大值为1,求函数的表达式,并写出函数图象的顶点坐标.
(2)若该函数的图象与x轴有且只有一个交点,求a,b的值.
(3)记(2)中的抛物线为y1,将抛物线y1向上平移2个单位得到抛物线![]() ,当
,当![]() 时,抛物线
时,抛物线![]() 的最大值与最小值之差为8,求m的值.
的最大值与最小值之差为8,求m的值.
22.(12分)![]() 年东京奥运会,中国跳水队赢得
年东京奥运会,中国跳水队赢得![]() 个项目中的
个项目中的![]() 块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板
块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板![]() 长为
长为![]() 米,跳板距水面
米,跳板距水面![]() 的高
的高![]() 为
为![]() 米,训练时跳水曲线在离起跳点水平距离
米,训练时跳水曲线在离起跳点水平距离![]() 米时达到距水面最大高度
米时达到距水面最大高度![]() 米,现以
米,现以![]() 为横轴,
为横轴,![]() 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.
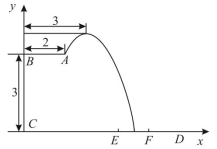
(1)![]() 时,求这条抛物线的解析式.
时,求这条抛物线的解析式.
(2)(1)的条件下,求运动员落水点与点![]() 的距离.
的距离.
(3)图中![]() 米,
米,![]() 米,若跳水运动员在区域
米,若跳水运动员在区域![]() 内(不含点
内(不含点![]() )入水时才能达到训练要求,求
)入水时才能达到训练要求,求![]() 的取值范围.
的取值范围.
23.(12分)已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与轴交于
两点,与轴交于![]() 点,点
点,点![]() 是抛物线上在第一象限内的一个动点,且点
是抛物线上在第一象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() .
.
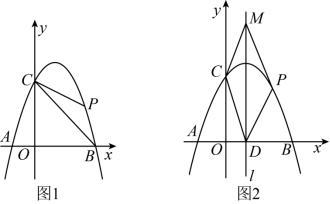
(1)求抛物线的表达式;
(2)如图1,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() .
.
①求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②求![]() 点到直线
点到直线![]() 的距离的最大值,并求出此时点P的坐标.
的距离的最大值,并求出此时点P的坐标.
(3)如图2,设抛物线的对称轴为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,直接写出点
是平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.









