初中数学湘教版九年级上册3.1 比例线段优质课课件ppt

这是一份初中数学湘教版九年级上册3.1 比例线段优质课课件ppt，共20页。PPT课件主要包含了建立一元二次方程模型，探究新知，整理得，方法点拨，针对训练，解设道路的宽为x米，还有其他解法吗，∴取x2，答道路的宽为2米，方法二等内容，欢迎下载使用。

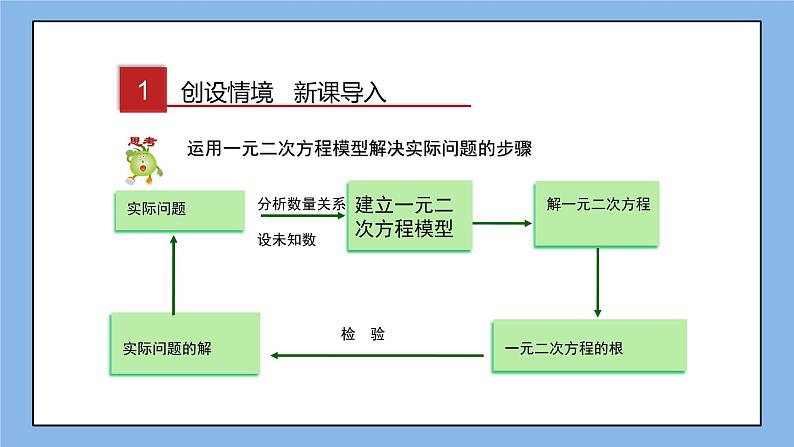
运用一元二次方程模型解决实际问题的步骤
创设情境 新课导入
某小区规划在一个长30m、宽20m的长方形土地上修建三条等宽的通道，使其中两条与AB平行，另外一条与AD平行，其余部分种花草，要使每一块花草的面积都为78m2，那么通道宽应该设计为多少？设通道宽为xm，则由题意列的方程为_ __________.
(30-2x)(20-x)=6×78
几何图形与一元二次方程
要设计一本书的封面,封面长27㎝,宽21cm正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度？(精确到0.1cm)
封面的长与宽之比为 ，中央矩形的长与宽之比也应是 ，由此判断上下边衬与左右边衬的宽度之比也是 设上、下边衬的宽均为9x cm，左、右边衬的宽均为7x cm，则中央矩形的长为cm，宽为_____________cm．
题 意：四周的彩色边衬所占面积是封面面积的四分之一，
等量关系：中央矩形的面积是封面面积的四分之三．
上、下边衬的宽均约为_______cm，左、右边衬的宽均约为________cm.
方程的哪个根合乎实际意义？为什么？
x2更合乎实际意义，如果取x1约等于2.799，那么上边宽为9×2.799＝25.191>21.
例1 如图，一块长和宽分别为40 cm，28 cm的矩形铁皮，在它的四角截去四个全等的小正方形，折成一个无盖的长方体盒子，使它的底面积为364 cm2. 求截去的小正方形的边长.
解：设截去的小正方形的边长为x cm，则无盖长方体盒子的底面边长分别为(40-2x)cm，(28-2x)cm. 根据题意，有 (40-2x)(28-2x)=364．
解得 x1=27，x2=7．
整理得， x2-34x+189=0.
如果截去的小正方形的边长为27cm，那么左下角和右下角的两个小正方形的边长之和为54cm，这超过了矩形铁皮的长40cm. 因此x1=27不合题意，应当舍去． 即所截去的小正方形的边长为7cm,
例2： 如图所示，在△ABC中，∠C=90°， AC=6cm，BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动；同时点Q沿CB边从点C向终点B以2cm/s的速度移动，且当其中一点到达终点时，另一点也随之停止移动.问点P，Q出发几秒后可使△PCQ的面积为9 cm²？
根据题意得AP= xcm,PC=(6-x)cm,CQ=2xcm
解：若设出发x s后可使△PCQ的面积为9cm²
解得 x1= x2=3
答：点P，Q出发3s后可使△PCQ的面积为9cm².
3、在几何图形的面积问题, 这类问题的面积公式是等量关系. 如果图形不规则应割或补成规则图形,找出各部分面积之间的关系,再运用规则图形的面积公式列出方程;
1、列一元二次方程解应用题的步骤与列一元一次方程解应用题的步骤类似，即审、设、列、解、检、答．
2、在列一元二次方程解应用题时，由于所得的根一般有两个，所以要检验这两个根是否符合实际问题的要求．
1、如图，在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少？
解：设道路的宽为 x 米
(32-x)(20-x)=540
整理，得x2-52x+100=0
解得 x1=2,x2=50
当x=50时，32-x=-18,不合题意，舍去.
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540㎡,求这种方案下的道路的宽为多少？
在宽为20m, 长为32m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为540m2,求这种种方案下的道路的宽为多少？
(32-2x)(20-x)=540
(32-2x)(20-2x)=540
解：设AB长是x m. (100-4x)x=400 x2-25x+100=0 x1=5，x2=20 x=20,100-4x=20<25 x=5,100-4x=80>25 x=5(舍去)答：羊圈的边长AB和BC的长个是20m,20m.
2、如图：要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB和BC的长个是多少米？
变式：如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80平方米？
解：设矩形猪舍垂直于住房墙的一边长为x m，
由题意得 x(25-2x+1)=80
化简，得 x2-13x+40=0
解得 x1=5 , x2=8
当x=5时，26-2x=16>12 (舍去）
当x=8时，26-2x=10<12
故所围矩形猪舍的长为10m,宽为8m.
则平行于住房墙的一边长(25-2x+1)m.
几何图形与一元二次方程问题
常见几何图形面积是等量关系.
常采用图形平移能聚零为整方便列方程
1. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的方程是（ ）A．x2+130x-1400=0 B．x2+65x-350=0C．x2-130x-1400=0 D．x2-65x-350=0
2.一块长方形铁板，长是宽的2倍，如果在4个角上截去边长为5cm的小正方形，  然后把四边折起来，做成一个没有盖的盒子，盒子的容积是3000 cm3，求铁板的长和宽．
解：设铁板的宽为x cm,则有长为2x cm
5(2x-10)(x-10)=3000x2-15x-250=0解得 x1=25 x2=-10(舍去）所以 2x=50
答：铁板的长50cm,宽为25cm.