2023九年级数学下册第二十七章相似章末培优专练作业课件新版新人教版

这是一份2023九年级数学下册第二十七章相似章末培优专练作业课件新版新人教版，共21页。

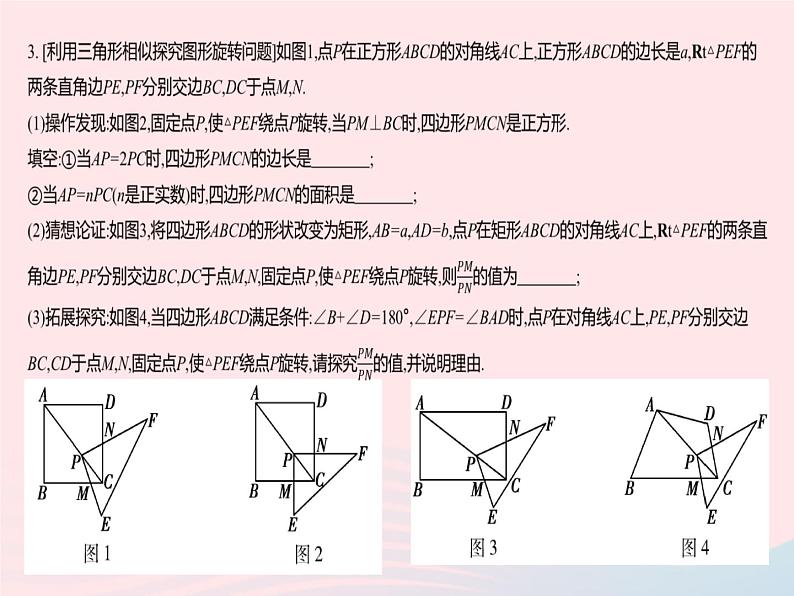
章末培优专练　　相似三角形是初中数学学科知识体系,特别是平面几何知识的重要组成部分,主要围绕逻辑推理、直观想象考查学生分析问题和解决问题的能力.如第2题,利用点对称构造相似三角形解决双动点问题,关注逻辑推理和直观想象;第3题,借助三角形相似探究图形旋转问题,关注逻辑推理.素养解读 答案 2. [利用点对称构造相似三角形解决双动点问题]如图,已知正方形ABCD的边长为3,点E在AB边上,且BE=1,点P,Q分别是边BC,CD上的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是　　　　. 答案  答案  1. [2021河北中考]图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB=(　　)A.1 cm B.2 cm C.3 cm D.4 cm答案 2. [2021重庆中考A卷]如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是(　　)A.1∶2 B.1∶4 C.1∶3 D.1∶9答案2.A　【解析】　∵△ABC与△DEF位似,点O为位似中心,∴△ABC∽△DEF,∴BC∶EF=OB∶OE=1∶2,∴△ABC与△DEF的周长之比为1∶2. 答案 4. [2020上海中考]《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为　　　　米. 答案 5. [2021山东菏泽中考]如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形BCME的面积比为　　　　　. 答案  答案  答案7.【解析】　(1)四边形BEDF为平行四边形.理由如下:∵四边形ABCD为平行四边形,∴AD∥BC,∠ABC=∠ADC.∵∠ABE=∠CDF,∴∠EBF=∠EDF.∵AD∥BC,∴∠EDF=∠DFC,∴∠DFC=∠EBF,∴BE∥DF,∴四边形BEDF为平行四边形.  答案