初中数学苏科版九年级上册第2章 对称图形——圆2.6 正多边形与圆优质教学课件ppt

这是一份初中数学苏科版九年级上册第2章 对称图形——圆2.6 正多边形与圆优质教学课件ppt，共15页。PPT课件主要包含了情境引入，它们的各角也相等，它们的各边相等，正三角形，正四边形，正五边形，正六边形，新课讲解，议一议，正多边形的特点等内容，欢迎下载使用。

问题：观看这些美丽的图案,都是在日常生活中我们经常能 看到的.你能从这些图案中找出类似的图形吗?
认真观察这些图形，每个图形有什么共同特点？
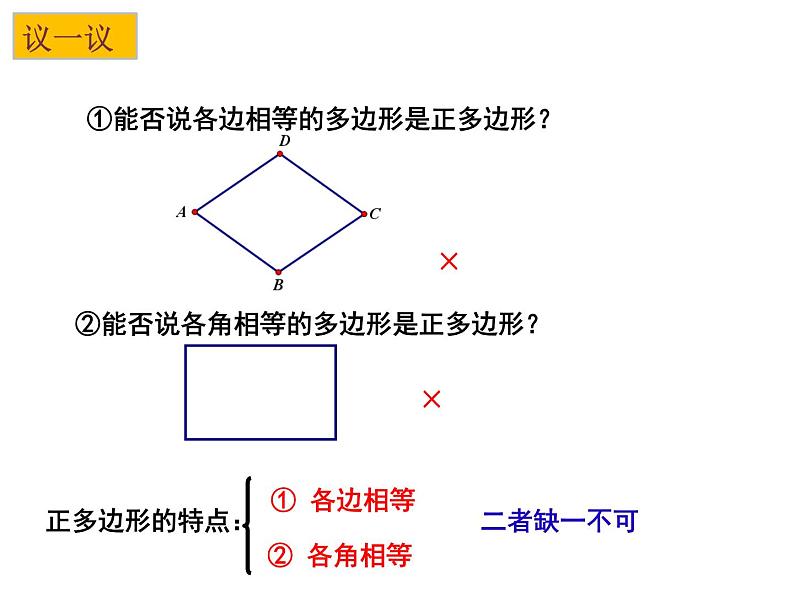
①能否说各边相等的多边形是正多边形？
　　②能否说各角相等的多边形是正多边形？
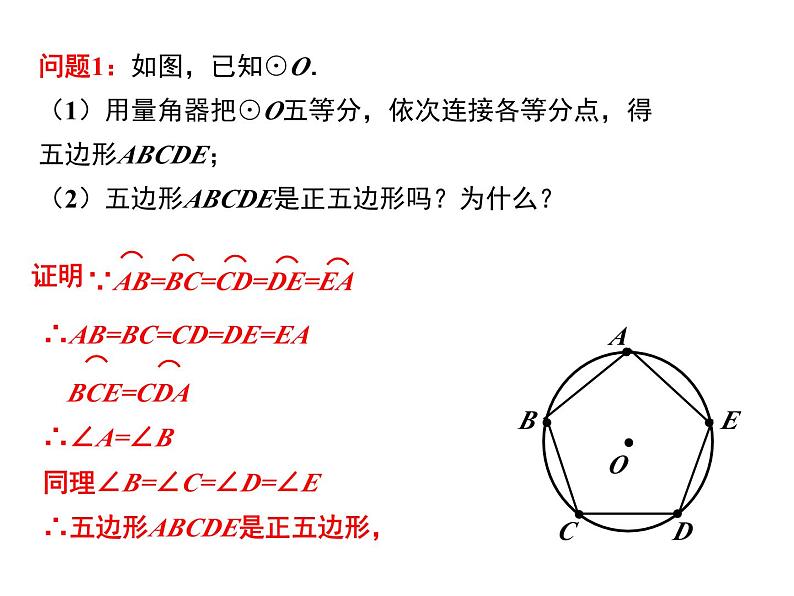
问题1：如图，已知⊙O．（1）用量角器把⊙O五等分，依次连接各等分点，得五边形ABCDE；（2）五边形ABCDE是正五边形吗？为什么？
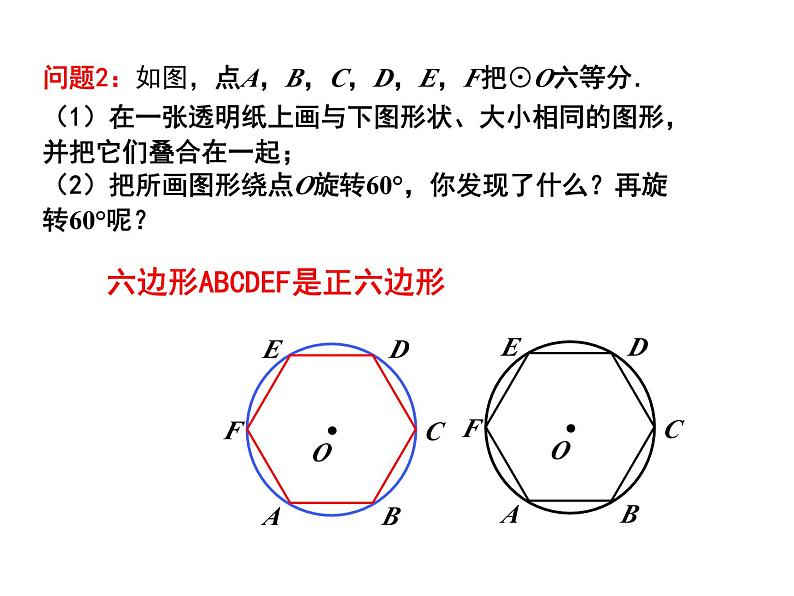
问题2：如图，点A，B，C，D，E，F把⊙O六等分．（1）在一张透明纸上画与下图形状、大小相同的图形，并把它们叠合在一起；（2）把所画图形绕点O旋转60°，你发现了什么？再旋转60°呢？
六边形ABCDEF是正六边形
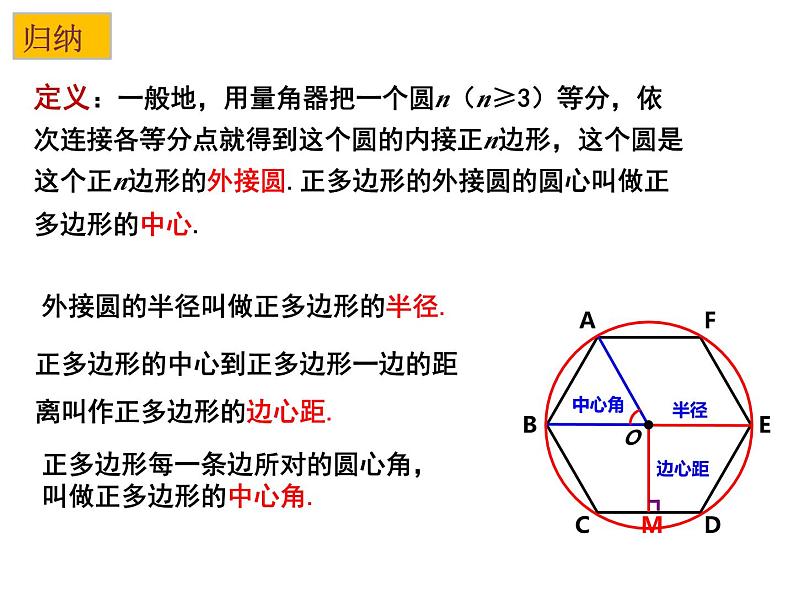
定义：一般地，用量角器把一个圆n（n≥3）等分，依次连接各等分点就得到这个圆的内接正n边形，这个圆是这个正n边形的外接圆.正多边形的外接圆的圆心叫做正多边形的中心.
外接圆的半径叫做正多边形的半径.
正多边形的中心到正多边形一边的距离叫作正多边形的边心距.
正多边形每一条边所对的圆心角，叫做正多边形的中心角.
例 如图，正六边形ABCDEF的半径为4.求这个正六边形的周长和面积.
问题1 正n边形的中心角怎么计算？
问题2 正n边形的边长a，半径R，边心距r之间有什么关系？
问题3 边长a，边心距r的正n边形的面积如何计算？
探 究 正多边形的有关计算
圆内接正多边形的辅助线
2.作边心距，构造直角三角形.
1.连半径，得中心角；
1.正六边形ABCDEF内接于⊙O，正六边形的周长是12，则⊙O的半径是（　　）
2.如图所示，正五边形ABCDE内接于⊙O，则∠ADE的度数是 （ ） A．60° B．45° C． 36° D． 30°
3.如图，已知⊙O的内接正六边形ABCDEF的边心距OM=2， 则该圆的内接正三角形ACE的面积为（　　）
4.如图，已知正五边形ABCDE，AF∥ CD，交DB的延长线于点F， 则∠DFA等于（　　）
A.30° B.36° C.45° D．32°
5．若一个正多边形的每个内角为150°，则这个正多边形的边数为 ．
6.已知正四边形的外接圆的半径为R，则正四边形的周长是 ．
7.如图，以正方形ABCD的AB边向外作正六边形ABEFGH，连接DH，则∠ADH= 度．
8.求证：正五边形的对角线相等.
证明： 在△BCD和△CDE中 ∵BC=CD ∠BCD=∠CDE CD=DE ∴△BCD≌△CDE ∴BD=CE 同理可证对角线相等.
已知：五边形ABCDE是正五边形.求证：DB=CE.
9.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.(1)求图①中∠MON=_______;图②中∠MON= ; 图③中∠MON= ;(2)试探究∠MON的度数与正n边形的边数n的关系.