第2章四边形复习题2课件（湘教版八下）

这是一份第2章四边形复习题2课件（湘教版八下），共24页。

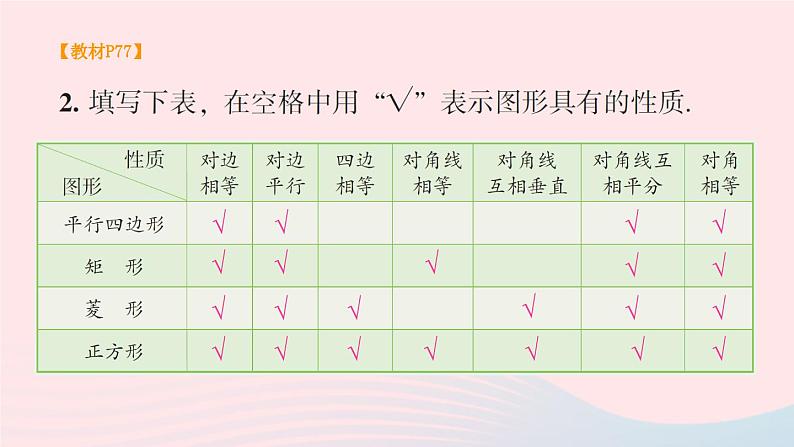
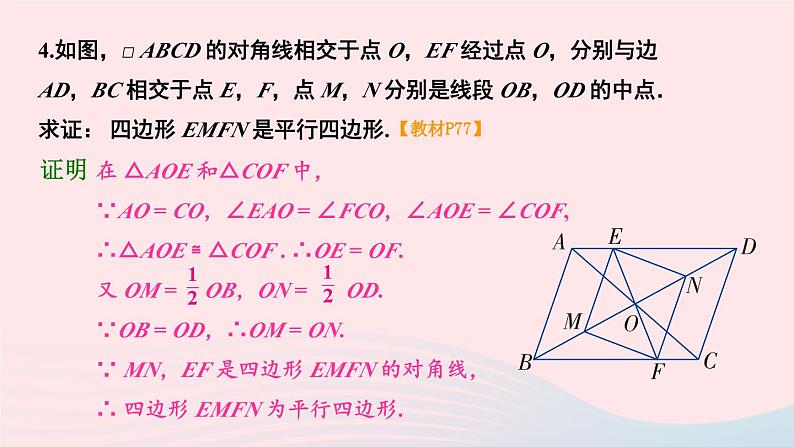
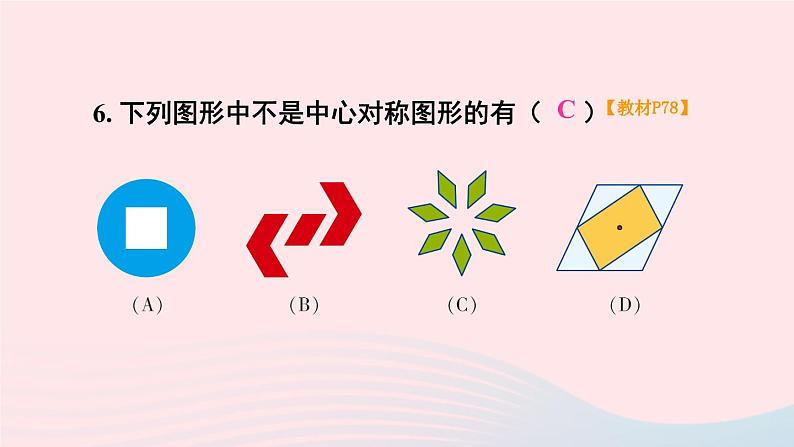
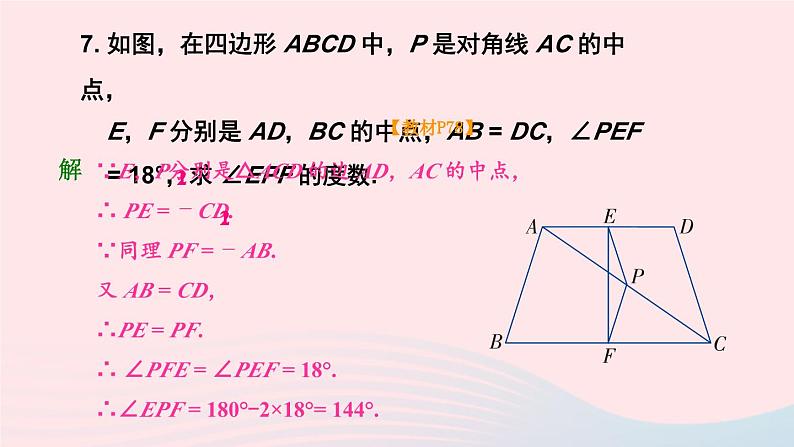
湘教·八年级下册【教材P77】解：（1）存在，设这个多边形的边数为 n. 根据题意，得解得 n ＝ 10，所以正十边形的每个角都等于相邻角的 4 倍.（2）不存在.【教材P77】√√√√√√√√√√√√√√√√√√√√√√【教材P77】解: 平行且平等.理由: ∵ 四边形 ABCD 是平行四边形,∴AB∥CD, AB ＝CD, ∴ ∠BAE ＝∠DCF.∵ CE ＝AF,∴ CE－EF ＝AF－EF,即CF ＝AE.在△ABE 和△CDF 中, AB ＝CD, ∠BAE ＝∠DCF, AE ＝CF, ∴ △ABE≌△CDF(SAS). ∴ BE ＝DF,∠AEB ＝∠CFD.∴ ∠BEF ＝∠DFE. ∴ BE∥DF. ∴ 线段BE 与 DF 平行且相等.4.如图，□ ABCD 的对角线相交于点 O，EF 经过点 O，分别与边 AD，BC 相交于点 E，F，点 M，N 分别是线段 OB，OD 的中点．求证： 四边形 EMFN 是平行四边形.在 △AOE 和△COF 中，∵AO = CO，∠EAO = ∠FCO，∠AOE = ∠COF,∴△AOE ≌ △COF . ∴OE = OF.又 OM = OB，ON = OD.∵OB = OD，∴OM = ON.∵ MN，EF 是四边形 EMFN 的对角线，∴ 四边形 EMFN 为平行四边形.证明 【教材P77】5.作出菱形 ABCD 关于 C 点成中心对称的图形.【教材P77】作法:（1）延长 DC 到点 D′, 使 D′C ＝ DC , 延长 AC 到 A′,使 A′C ＝ AC , 延长 BC 到 B′C，使B′C ＝ BC.（2）连接 A′B′ , A′D′ , 则菱形 A′B′CD′ 就是所求作的菱形ABCD 关于 C 点成中心对称的图形.6. 下列图形中不是中心对称图形的有（ ）【教材P78】C7. 如图，在四边形 ABCD 中，P 是对角线 AC 的中点， E，F 分别是 AD，BC 的中点，AB = DC，∠PEF = 18°，求 ∠EPF 的度数.∵E，P分别是△ACD 的边 AD，AC 的中点，∴ PE = CD.∵同理 PF = AB.又 AB = CD，∴PE = PF.∴ ∠PFE = ∠PEF = 18°.∴∠EPF = 180°-2×18°= 144°.解 【教材P78】【教材P78】解:如右图所示,在矩形 ABCD 中, AC ＝ 2 cm, 所以 AO ＝ 1 cm.∵∠BOC ＝ 120°,∴∠AOB ＝ 180°－∠BOC ＝ 60°.∵ AC ＝BD, OA ＝ AC, OB ＝ BD, ∴ OA ＝ OB.∴△AOB 是等边三角形.∴BO ＝AO ＝AB ＝1 cm.∵∠ABC ＝ 90°, 在 Rt△ABC 中,由勾股定理,得 BC ＝∴矩形 ABCD 的周长为9. 两条平行线被第三条直线所截，两组内错角的平分线 相交所成的四边形是矩形吗？为什么？【教材P78】是距形.理由：∵ EF∥MN，∴ ∠FAC +∠NCA = 180°.又∠1 = ∠FAC，∠2 = ∠NCA，∴∠1+∠2 = (∠FAC+∠NCF) = 90°.∴ ∠D = 90°. 同理可得 ∠B = 90°.又∠BAD = ∠1+∠BAC = ∠FAC + ∠CAF= ×180°= 90°∴四边形 ABCD 是矩形.解 【教材P78】解:（1）四边形 ABCD 是菱形, 因为四边形 ABCD 的四条边相等.【教材P78】（2）在菱形 ABCD 中,AC⊥BD,AC ＝AB ＝2 cm,AO ＝ AC ＝ ×2＝1(cm).∴ 在 Rt△AOB 中,BO ＝ .∴ BD ＝2BO ＝ cm, ∴ 四边形 ABCD 的两条对角线的长度分别是 2 cm, cm.【教材P78】∴ 四边形 ABCD 的面积是 cm2.11. 如图，四边形 ABCD 是正方形， △EBC 是等边三角形， 求∠AED.【教材P78】∵ 四边形 ABCD 是正方形，∴ AB = BC，∠ABC = 90°.∵ △EBA 是等边三角形，∴EB = BC = EC，∠EBC=∠BEC= 60°.∴ EB = AB，∠ABE = 90°-60°=30°. ∴∠BAE= ∠BEA = 75°. 同理 ∠CED = 75°.∴∠ AED = 360°-75°-75°-60°= 150°.解 【教材P78】解析: 直线将四边形分割成两个三角形,它们的内角和为 360°,分割成一个三角形,一个四边形,它们的内角和为540°,分割成两个四边形,它们的内角和为720°，分割成一个三角形,一个五边形,它们的内角和为720°. 所以不可能得到 630°.D【教材P79】解: EF 与 MN 互相平分. 理由如下: 因为四边形 ABCD 是平行四边形,∴ AB∥CD,AB ＝CD.又∵ BE ＝DF,∴ 四边形 BFDE 为平行四边形,∴ BF∥DE.同理四边形 AECF 是平行四边形,∴ AF∥EC.∴ 四边形EMFN是平行四边形, ∴ EF 与 MN 互相平分.【教材P79】证明:∵ 矩形 ABCD 和矩形 A′B′C′D 关于点 D 成中心对称,∴ A′D ＝AD , C′D ＝CD.∴ 四边形 ACA′C′ 是平行四边形.又∵ ∠ADC ＝ 90°,即 AA′⊥CC′,∴ 四边形 ACA′C′ 是菱形(对角线互相垂直的平行四边形是菱形).【教材P79】解:如图所示,连接 AC, BD 相交于点 O. 在正方形 ABCD 中,∵ ∠DOC ＝ 90°, ∴ ∠COF ＋∠DOF ＝90°.∵ 在正方形 A′OC′D′ 中, ∠A′OC′ ＝90°,∴ ∠DOE＋∠DOF ＝90°.∴ ∠COF ＝∠DOE. 又∵ ∠OCF ＝∠ODE ＝45°, OC ＝OD.∴ △OCF≌△ODE (ASA),【教材P79】解:（1）当E,F,G,H 分别是四边形 ABCD 各边的中点时,得到四边形 EFGH 是平行四边形.理由: 连接对角线 BD, 则 EH∥BD, EH ＝ BD.同理, FG∥BD,FG ＝ BD,所以 EH∥FG,EH ＝ FG,故四边形 EFGH 是平行四边形.【教材P79】（2）当四边形 ABCD 是矩形时,四边形 EFGH 是菱形.理由: 由于四边形 ABCD 是矩形,可得 △AEH ≌ △BEF ≌ △CGF ≌ △DGH.从而得 EH ＝ EF ＝ GF ＝ GH,所以四边形 EFGH 是菱形.【教材P79】（3）当四边形 ABCD 是菱形时,四边形EFGH 是矩形.理由:由（1）得四边形EFGH 是平行四边形.连接EG,FH,可得四边形 AEGD 是平行四边形,所以 EG ＝AD.同理 FH ＝AB.由AB ＝AD,得EG ＝FH,所以四边形 EFGH 是矩形(对角线相等的平行四边形是矩形).【教材P79】（4）当四边形 ABCD 是正方形时,四边形 EFGH 也是正方形.理由:由（2）（3）可证明四边形 EFGH 既是矩形,又是菱形, 故四边形 EFGH 是正方形.【教材P79】解:∵ DE∥BC, ∴ ∠DEF ＝∠EFB.∵ M,N 是矩形 ABCD 的边 AB, CD 的中点,∴ EA ＝AF.∵ ∠BAE ＝ 90°，∴ ∠BAE ＝∠BAF ＝90°.在△BAE 和△BAF 中 AE ＝AF,∠BAE ＝∠BAF , AB ＝AB.∴ △BAE≌△BAF(SAS). ∴ ∠BEA ＝∠BFE.又∠DEF ＝∠EFB , ∴ ∠BEA ＝∠DEA.由于以 E 为顶点在 ED 边及 ED 边的反向延长线上的三个角构成一个平角且这三个角相等.