八数湘教版下册 2.2 平行四边形 PPT课件+教案+练习

2.2.1  平行四边形的性质（1）

【学习目标】

1、理解并掌握平行四边形的定义；掌握平行四边形的性质定理1及性质定理2（重点）。

2、理解两条平行线的距离的概念。

3、经历探索平行四边形的有关概念和性质的过程， 发展自己的探究意识和合情推理的能力（难点）。

【学习过程】

一、学前准备：

1、什么是四边形？四边形的一组对边有怎样的位置关系？

2、一般四边形有哪些性质？

二、合作探究：

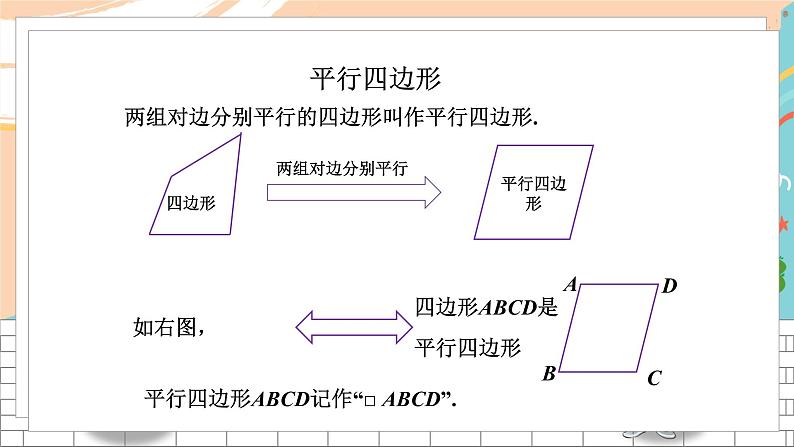
1、平行四边形的定义：

（1）定义：两组对边分别平行的四边形叫作平行四边形。

（2）定义的双重性：具备“两组对边分别平行”的四边形，才是“平行四边形”，反过来，“平行四边形”就一定具有“两组对边分别平行”的性质。

（3）平行四边形的表示：用______表示，如_______ABCD.

2、探究平行四边形的性质：

探究： 已知：如图1，四边形ABCD是平行四边形，

求证：AB＝CD，CB＝AD，∠B＝∠D，∠BAD＝∠BCD．

        （图1）

结论   性质1：平行四边形的对边相等。

性质2：平行四边形的对角相等。

3、两条平行线间的距离：

推论：夹在两条平行线间的平行线段相等。

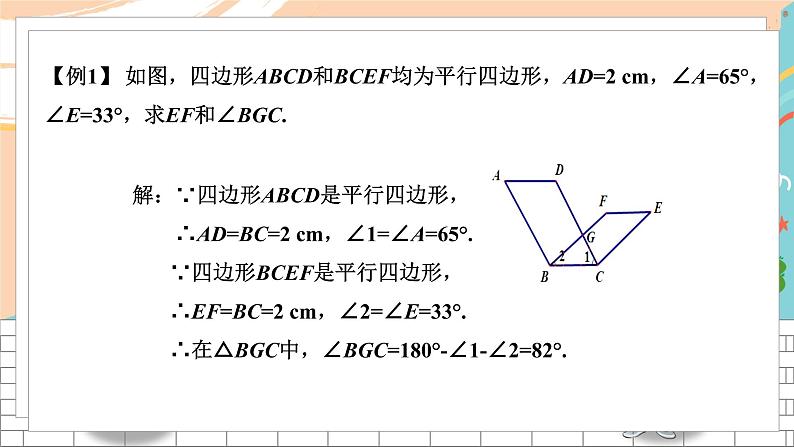
三、应用与迁移

例1：（1）在平行四边形ABCD中，∠A=500，求∠B、∠C、∠D的度数。

（2）平行四边形的两邻边长的比是2：5，周长为28cm，求平行四边形各边的长。

【学习小结】：

1、我的收获：

2、我的困惑：

【学习检测】

基础练习：

1．如图2，在平行四边形ABCD中，AC为对角线，BE⊥AC，DF⊥AC，E、F为垂足，

求证：BE＝DF。

2、如图3，在平行四边形ABCD中，如果EF∥AD，GH∥CD，EF与GH相交于点O，那么图中的平行四边形一共有（   ）．

（A）4个     （B）5个     （C）8个     （D）9个

        （图2）                （图3）               （图4）

拓展练习：

3、如图4，AD∥BC，AE∥CD，BD平分∠ABC。

求证：AB=CE。

4、农民李某想发展副业致富，考察地形后，在耕地旁边的荒地上开垦一块平行四边形形状的鱼塘。测得∠BAD＝1200，量得AB＝50米，AD＝80米。请你帮助李某计算鱼塘的对边AD、BC之间的距离及这个鱼塘的面积。

课后反思：

2.2.1  平行四边形的性质（2）

【学习目标】

1、掌握平行四边形对角线互相平分这一性质，并会用此性质进行有关的论证和计算（重点）。

2、经历观察、猜想、实验、验证等数学活动，认识平行四边形的性质。

3、通过多种方法探究平行四边形的性质，体验解决问题策略的多样性（难点）。

【学习过程】

一、学前准备：

复习：四边形的内角和、外角和定理？ 平行四边形的性质定理1、2的内容？ 什么叫两条平行线的距离？

二、合作探究：

探究：如图1，▱ ABCD的两条对角线AC，BD相交于点O，

1、图中有哪些三角形是全等的？哪些线段是相等的？

2、能设法验证你的猜想吗？

3、你能发现平行四边形的对角线有什么性质？

性质3：平行四边形的对角线互相平分。

三、应用与迁移

1、从边、角、对角线总结平行四边形的性质：

  从边看：_____________________________________________________________。

  从角看：________________________________________________________________。

  从对角线看：_____________________________________________________________。

2、已知▱ ABCD的两条对角线AC，BD相交于点O，AB⊥AC，AB=3，AD=5，求BD的长。

【学习小结】：

1、我的收获：

2、我的困惑：

【学习检测】

基础练习：

1、课本练习1、2。

拓展练习：

2、在▱ABCD中，已知AC、BD相交于点O，两条对角线的和为24cm,BC的长为8cm，求△AOD的周长。

3、如图，D是等腰三角形ABC的底边BC上的一点，E、F分别在AC、AB上，且DE∥AB， DF∥AC．试问：DE、DF与AB之间有什么关系?请说明理由．

课后反思：

2.2.2   平行四边形的判定

【学习目标】

1.掌握平行四边形的判定定理1、2、3，并能与性质定理、定义综合运用（重点）。

2.使学生理解判定定理与性质定理的区别与联系（难点）。

3.会根据简单的条件画出平行四边形，并说明画图的依据是哪几个定理。

【学习过程】

一、学前准备：

1、平行四边形的定义：_____________________________________________________。

2、平行四边形有什么性质？               

二、合作探究：

1、动手试一试：将线段AB按图中所给的方向和距离，平移成线段CD，构成一个一组对边平行且相等的四边形ABCD，你能说出它一定是平行四边形吗？为什么？

                                      D                C

                              A                    B

2、探究归纳：

平行四边形的判定定理1：____________________________________________________。

平行四边形的判定定理2：____________________________________________________。

平行四边形的判定定理3：____________________________________________________。

三、应用与迁移

例1  已知：如图，E、F是▱ ABCD的对角线AC上两点，且AE=CF。

求证：四边形BEDF是平行四边形。

    D                   C

                  F

       E

A               B

【学习小结】：

1、我的收获：

2、我的困惑：

【学习检测】

基础练习：

1、下面给出了四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是（　　）

A.1：2：3：4　    B.2：2：3：3

C.2：3：2：3　    D.2：3：3：2

2、下面给出的条件，能判定一个四边形是平行四边形的是（　）

Ａ.一组对边平行，另一组对边相等　   Ｂ.一组对边平行，一组对角互补

Ｃ.一组对角相等，一组邻角互补　 　  Ｄ.一组对角相等，另一组对角互补

3、用两个全等的三角形按不同的方法拼成四边形，在这些拼出的四边形中，平行四边形最多有（　　）

A．1个　 　B．2个　  　C．3个　  　D．4个

4、已知：如图，在平行四边形ABCD中，E、F分别是AB，DC上的两点，且AE＝CF．

求证：BD，EF互相平分。                                             

                                                        D                  C

A     E           B

拓展练习：

5、已知在平行四边形ABCD中，G、H分别是AB，CD的中点，点E、F在AC上，且

AE＝CF．求证：四边形EGFH是平四边形．

课后反思：