第8章认识概率复习课件

这是一份第8章认识概率复习课件，共17页。

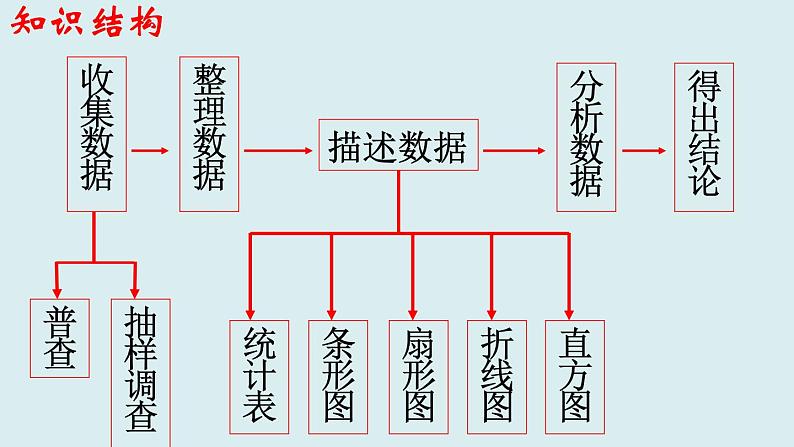
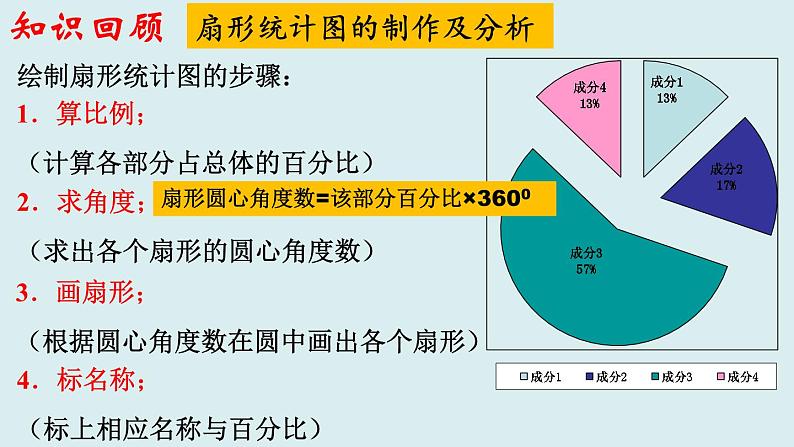
2022第七章 数据的收集、整理、描述八年级下册知识结构收集数据整理数据描述数据条形图扇形图折线图直方图分析数据得出结论统计表普查抽样调查普查： 抽样调查：为一特定目的而对所有考察对象所做的全面调查。为一特定目的而对部分考察对象所做的调查相关概念：总体，个体，样本，样本容量。（1）普查的调查结果准确，但工作量大，难度大，而且有些调查具有破坏性不宜使用普查。（2）抽样调查的工作量较小，便于进行；但其调查结果不准确，应注意选取的样本的全面性和代表性。优缺点：知识回顾普查与抽样调查D调查对象多，适合抽样调查具有破坏性，适合抽样调查涉及重大安全问题，适合普查典例分析关注调查方式的选择1．要调查下面的问题：　 ①调查学校营养餐牛奶的质量情况； ②调查你们班学生早餐是否有喝牛奶的习惯； ③调查全国中学生的节水意识； ④调查某校七年级学生的视力情况， 其中适合采用普查的是＿＿＿＿＿＿＿．（填写序号）②，④调查对象多，适合抽样调查具有破坏性，适合抽样调查巩固小练关注调查方式的选择总体、个体、样本、样本容量的理解典例分析例2 为了解某校600名八年级学生的身高，随机抽测了100名学生的身高，在这个问题中，总体是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿， 个体是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿， 样本是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿， 样本容量是＿＿＿＿＿＿＿＿．该校600名八年级学生每个八年级学生的身高从中抽测的100名八年级学生的身高100样本容量是数值，无单位考察对象是指“数”，而不是“物”××的身高的全体名1．为了了解我市2019年40 000名考生的数学中考成绩，从中抽取 了2 000名考生的成绩进行统计，在这个问题中，下列说法： ①这40 000名考生的数学中考成绩的全体是总体； ②每个考生是个体； ③从中抽取的2 000名考生的数学中考成绩是总体的一个样本； ④样本容量是2 000． 其中说法正确的有___________．（填序号）每个考生的数学中考成绩是个体√√√①，③，④总体、个体、样本、样本容量的理解巩固练习×知识回顾扇形统计图的制作及分析扇形圆心角度数=该部分百分比×3600绘制扇形统计图的步骤：1．算比例；（计算各部分占总体的百分比）2．求角度；（求出各个扇形的圆心角度数）3．画扇形；（根据圆心角度数在圆中画出各个扇形）4．标名称；（标上相应名称与百分比）1、某班有50人，其中三好学生10人，优秀学生干部5人，在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是（ ）A．720，360 B．1000，500 C．1200，600 D．800，400 2、如图，某校共有学生700人，图中扇形A、B、C、分别表示参加语、数、英三个兴趣小组的人数的百分比，规定每人只能参加一个兴趣小组且每人均参加课外小组，则不参加数学小组的学生有（ ）A．441人 B．259人 C．451人 D．249人AA巩固练习扇形统计图的制作及分析知识回顾统计图的特点及选用条形统计图能清楚 地表示出每个项目的具体数目。折线统计图能清楚 地反映事物的变化情况。扇形统计图能清楚地表示出各部分在总体中所占的百分比。1、要清楚地表明一病人的体温变化情况，应选择的统计图是（ ）A．扇形统计图 B．条形统计图 C．折线统计图 D．以上都不是2、某音乐行出售三种音乐CD，即古典音乐、流行音乐、民族音乐，为了表示这三种音乐唱片的销售量的百分比，应该用（ ）A．扇形统计图 B．折线统计图 C．条形统计图 D．以上都可以 CA巩固练习统计图的特点及选用巩固练习统计图的综合应用1、某校为了了解学生对中国民族乐器的喜爱情况，随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种乐器)，现将收集到的数据绘制成如图所示的两幅不完整的统计图。(1)这次共抽取 名学生进行调查，扇形统计图中的 x = ;20015%(2)请补全条形统计图:(3)在扇形统计图中“扬琴”所在扇形的圆心角是 度;(4)若该校有3000名学生，请你估计该校喜爱“二胡”的学生约有 名.3690060巩固练习统计图的综合应用知识回顾频数、频率、频数分布直方图某个对象出现的次数频数：频率：频数与总次数的比值频率 = 频数=总次数×频率 总次数=各个对象出现的频数之和等于总次数. 各个对象出现的频率之和等于1. 1.算：计算最大值与最小值的差2.定：决定组距与组数3.划：利用划记法 得到各组频数4.列：列出频率分布表5.绘：绘制出直方图绘制频数分布直方图的基本步骤：知识回顾频数、频率、频数分布直方图1、已知一个样本： 27，23，25，27，29，31，27，30，32，28，31，28，26，27，29，28，24，26，27，30那么频数为 8 的范围是( ) A ．24.5 ~26.5 B．26.5~28.5 C．28.5~30.5 D．30.5~32.5 2、在1000个数据中，用适当的方法抽取50个作为样本进行统计，频率分布表中54.5~57.5这一组的频率是0. 12，那么估计总体数据落在54.5~57.5 之间的约有( ) A．120个 B．60个 C．12个 D．6个BA巩固练习频数、频率、频数分布直方图3、某校为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：根据以上图表信息，解答下列问题：（1）表中的a＝_____， b＝______;（2）请把频数分布直方图补充完整;（3）若该校共有1 200名学生，请估计该校在上学期参加社区活动 超过6次的学生有多少人？巩固练习频数、频率、频数分布直方图12 0.08 672