小学数学二 圆柱和圆锥教案

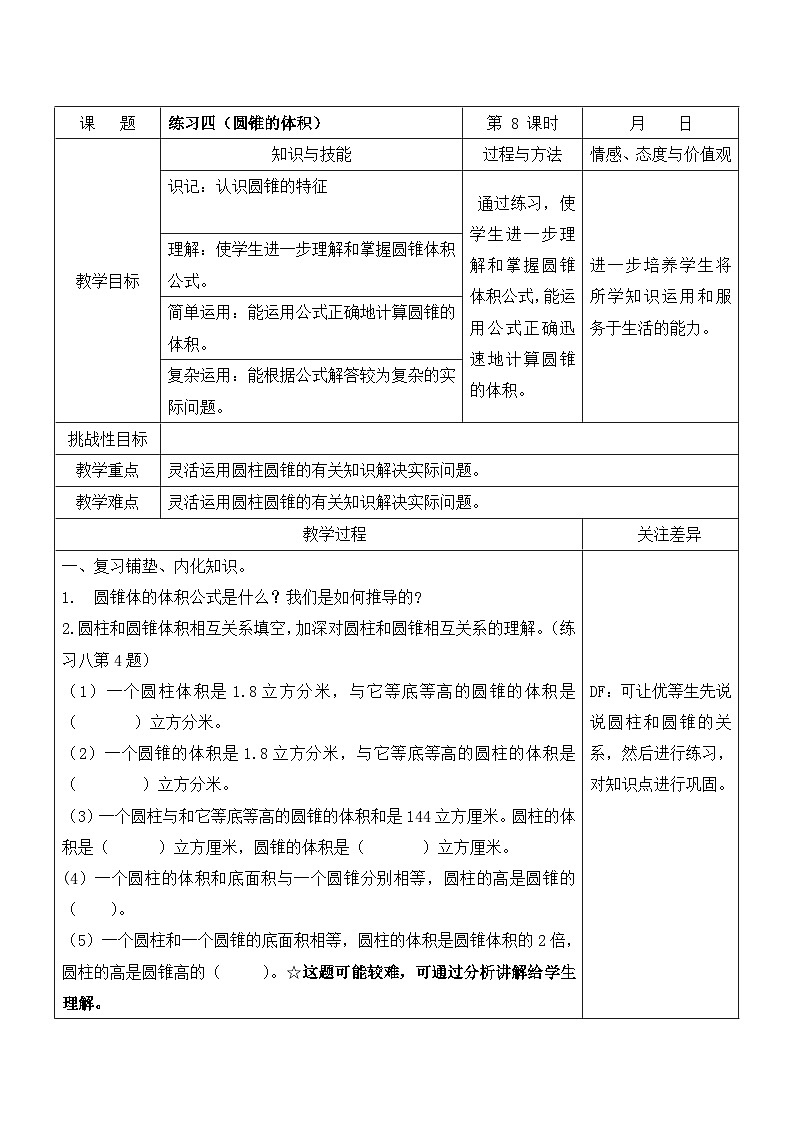
课   题

练习四（圆锥的体积）

第 8 课时

月    日

教学目标

知识与技能

过程与方法

情感、态度与价值观

识记：认识圆锥的特征

通过练习，使学生进一步理解和掌握圆锥体积公式，能运用公式正确迅速地计算圆锥的体积。

进一步培养学生将所学知识运用和服务于生活的能力。

理解：使学生进一步理解和掌握圆锥体积公式。

简单运用：能运用公式正确地计算圆锥的体积。

复杂运用：能根据公式解答较为复杂的实际问题。

挑战性目标

教学重点

灵活运用圆柱圆锥的有关知识解决实际问题。

教学难点

灵活运用圆柱圆锥的有关知识解决实际问题。

教学过程

关注差异

一、复习铺垫、内化知识。

1.　圆锥体的体积公式是什么？我们是如何推导的?

2.圆柱和圆锥体积相互关系填空，加深对圆柱和圆锥相互关系的理解。（练习八第4题）

（1）一个圆柱体积是1.8立方分米，与它等底等高的圆锥的体积是（       ）立方分米。

（2）一个圆锥的体积是1.8立方分米，与它等底等高的圆柱的体积是（        ）立方分米。

（3）一个圆柱与和它等底等高的圆锥的体积和是144立方厘米。圆柱的体积是（      ）立方厘米，圆锥的体积是（       ）立方厘米。

(4）一个圆柱的体积和底面积与一个圆锥分别相等，圆柱的高是圆锥的（    ）。

（5）一个圆柱和一个圆锥的底面积相等，圆柱的体积是圆锥体积的2倍，圆柱的高是圆锥高的（     ）。☆这题可能较难，可通过分析讲解给学生理解。

(6)把一个圆柱削成一个最大的圆锥，削去部分的体积相当于圆柱的（    ） ，相当于圆锥的(   )倍。

(7)圆柱体的侧面展开可以得到一个长方形, 这个长方形的长等于圆柱的（               ）, 宽等于圆柱的(　 )。

（8）圆柱体积比与它等底等高的圆锥体积大(　　 )倍。

(9）圆锥体积比与它等底等高的圆柱体积少（  　）。

3.求下列圆锥体的体积。

（1）底面半径4厘米，高6厘米。

（2）底面直径6分米，高8厘米。

（3）底面周长31.4厘米.高12厘米。

4、教师根据学生练习中存在的问题，集体评讲。

二、完成书上部分练习。

1、完成31页第5题。讨论下列问题：

 （1）圆柱和圆锥体积相等、底面积也相等，圆柱的高和圆锥的高有什么关系？

（2）圆柱和圆锥体积相等、高也相等，圆柱的底面积和圆锥的底面积有什么关系？

2、分组讨论：圆柱的底面半径是圆锥的2倍，圆锥的高是圆柱的高的2倍，圆柱和圆锥的体积之间有什么倍数关系？

3、讨论练习八第9题。

蒙古包所占空间的大小的方法。

（1） 蒙古包是由哪几个部分组成的？

（2） 上部的圆锥和下部的圆柱有哪些相同的地方，有哪些不同的地方？

（3） 同学们能独立地求出蒙古包所占的空间的大小吗？请试一试。

4、完成练习八第6题。

让学生独立完成。提问：能削成的最大圆锥是怎样的？还可以提什么问题呢？（提示还可以求削去部分的面积。）

5、完成练习八第7、8题。

学生独立完成后核对答案。

6、教学生如何测量圆锥的高。

7、交流一下本节课的收获。

三、丰富拓展、延伸练习。

1、书上思考题：

一个圆锥和一个圆柱的底面积相等，体积的比是1:6。如果圆锥的高是4.2厘米，圆柱的高是多少厘米？如果圆柱的高是4.2厘米，圆锥的高是多少厘米？

2、拓展练习：

(1)把一个圆柱体木料削成一个最大的圆锥体木料， 圆锥的体积占圆柱体的几分之几？削去的部分占圆柱体的几分之几？

（2）一个圆柱体比它等底等高的圆锥体积大48立方厘米，圆柱体和圆锥

DF：可让优等生先说说圆柱和圆锥的关系，然后进行练习，对知识点进行巩固。

DF：巩固练习的题目跟生活实际密切联系，通过练习，让更多学生会解答此类题目。

体的体积各是多少？

四、全课总结，内化知识。

1.提问:

(1)同学们掌握了圆锥体的哪些知识？

(2)你用圆锥体的体积的有关知识解决现实生活中的哪些问题？

五、作业设计。

课堂作业：《补充习题》P18

回家作业：《练习与测试》P20-21

板书设计：              圆锥的体积

等底 等高

圆锥的体积=底面积×高÷3

教后反思：