高中人教A版 (2019)第二章 直线和圆的方程2.5 直线与圆、圆与圆的位置精品课后测评

这是一份高中人教A版 (2019)第二章 直线和圆的方程2.5 直线与圆、圆与圆的位置精品课后测评，文件包含251直线与圆的位置关系-2023-2024学年高二数学同步精品讲义人教A版2019选择性必修第一册解析版docx、251直线与圆的位置关系-2023-2024学年高二数学同步精品讲义人教A版2019选择性必修第一册原卷版docx等2份试卷配套教学资源，其中试卷共79页， 欢迎下载使用。

2.5.1 直线与圆的位置关系

课程标准
核心素养
1.能根据给定直线、圆的方程，判断直线与圆的位置关系．
2.能用直线和圆的方程解决一些简单的问题．体会用代数方法处理几何问题的思想.
直观想象
数学运算





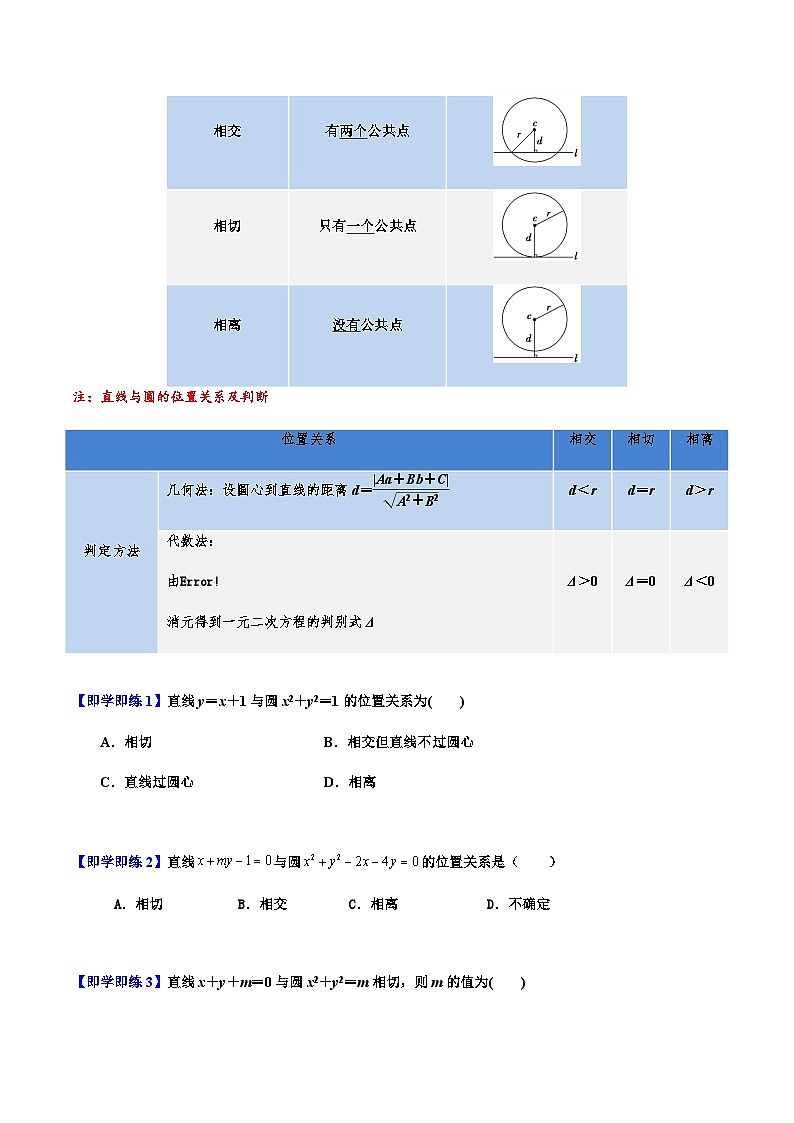
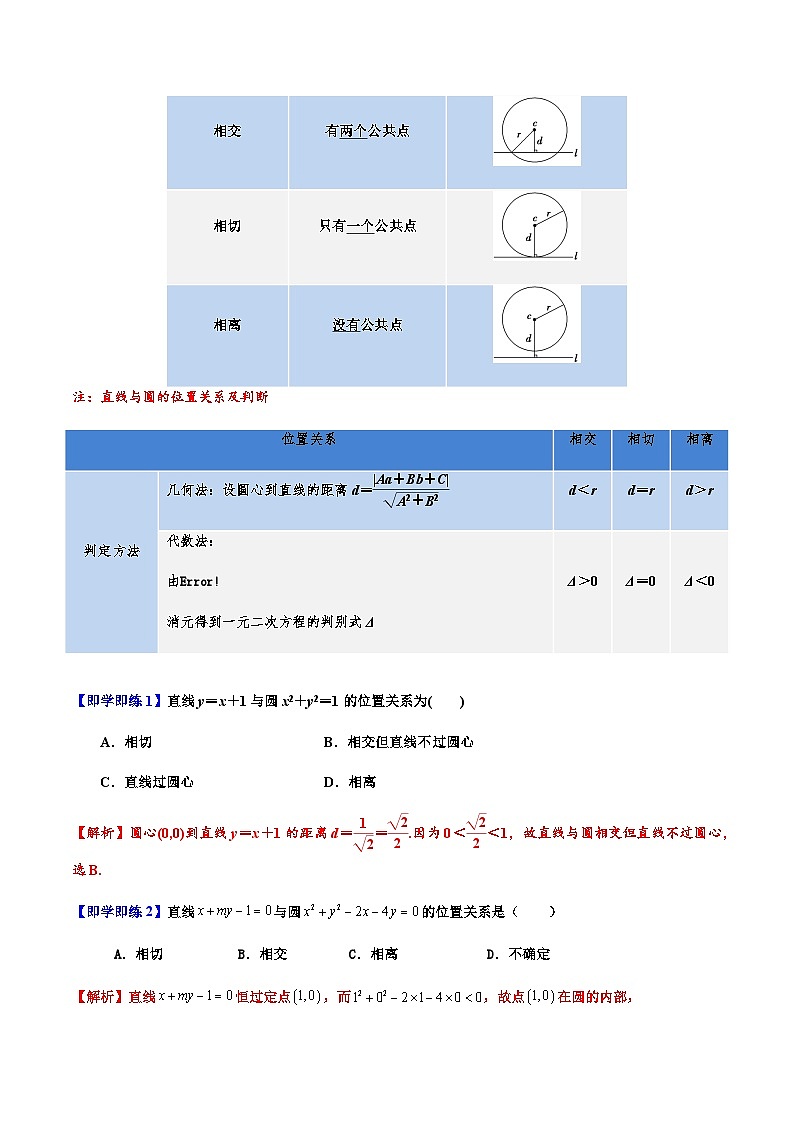
知识点1 直线与圆的三种位置关系
位置关系
交点个数
图示
相交
有两个公共点

相切
只有一个公共点

相离
没有公共点

注：直线与圆的位置关系及判断
位置关系
相交
相切
相离
判定方法
几何法：设圆心到直线的距离d＝
d＜r
d＝r
d＞r
代数法：
由
消元得到一元二次方程的判别式Δ
Δ＞0
Δ＝0
Δ＜0

【即学即练1】直线y＝x＋1与圆x2＋y2＝1的位置关系为(　　)
A．相切　　　　　　　 B．相交但直线不过圆心
C．直线过圆心 D．相离
【解析】圆心(0,0)到直线y＝x＋1的距离d＝＝.因为0＜＜1，故直线与圆相交但直线不过圆心，选B.
【即学即练2】直线与圆的位置关系是（  ）
A．相切 B．相交 C．相离 D．不确定
【解析】直线恒过定点，而，故点在圆的内部，
故直线与圆的位置关系为相交，
故选：B.

【即学即练3】直线x＋y＋m＝0与圆x2＋y2＝m相切，则m的值为(　　)
A．0或2 B．2
C. D．无解
【解析】由于直线与圆相切，故＝，解得m＝0(舍去)或m＝2.
【即学即练4】已知圆经过，，且圆心在直线上.
(1)求圆的标准方程；
(2)若直线：与圆无公共点，求实数的取值范围.
【解析】(1)∵圆心C在直线，
∴可设圆心坐标为，
∵圆C经过，，
∴即，解得
∴圆心坐标为，半径
故圆C的标准方程为；
(2)∵圆心C到直线l的距离且直线l圆C无公共点，
∴即，解得，
故实数k的取值范围为；
综上，圆C的标准方程为，.


知识点2 直线与圆相交
1．解决圆的弦长问题的方法

几何法
（常用）

如图所示，设直线l被圆C截得的弦为AB，圆的半径为r，圆心到直线的距离为d，则有关系式：|AB|＝2
代数法
若斜率为k的直线与圆相交于A(xA，yA)，B(xB，yB)两点，则|AB|＝·＝·|yA－yB|(其中k≠0)．特别地，当k＝0时，|AB|＝|xA－xB|；当斜率不存在时，|AB|＝|yA－yB|
注：直线：；圆
联立消去“”得到关于“”的一元二次函数，结合韦达定理可得到
2．当直线与圆相交时，半径、半弦、弦心距所构成的直角三角形(如图中的Rt△ADC)，在解题时要注意把它和点到直线的距离公式结合起来使用．
【即学即练5】直线y＝2x＋3被圆x2＋y2－6x－8y＝0所截得的弦长等于________．
【解析】圆的方程可化为(x－3)2＋(y－4)2＝25.故圆心为(3,4)，半径r＝5.又直线方程为2x－y＋3＝0，所以圆心到直线的距离为d＝＝，所以弦长为2＝2×＝2＝4.

知识点3 直线与圆相切
1．求过某点的圆的切线问题时，应首先确定点与圆的位置关系，再求切线方程．若点在圆上(即为切点)，则过该点的切线只有一条；若点在圆外，则过该点的切线有两条，此时应注意切线斜率不存在的情况．（注：过圆内一点，不能作圆的切线）
2．求过圆上的一点(x0，y0)的切线方程的方法
先求切点与圆心连线的斜率k，若k不存在，则结合图形可直接写出切线方程为y＝y0；若k＝0，则结合图形可直接写出切线方程为x＝x0；若k存在且k≠0，则由垂直关系知切线的斜率为－，由点斜式可写出切线方程．
3．求过圆外一点(x0，y0)的圆的切线方程的方法
几何法
当斜率存在时，设为k，则切线方程为y－y0＝k(x－x0)，即kx－y＋y0－kx0＝0.由圆心到直线的距离等于半径，即可求出k的值，进而写出切线方程
代数法
当斜率存在时，设为k，则切线方程为y－y0＝k(x－x0)，即y＝kx－kx0＋y0，代入圆的方程，得到一个关于x的一元二次方程，由Δ＝0，求得k，切线方程即可求出
4.圆的切线方程常用结论
(1)过圆x2＋y2＝r2上一点P(x0，y0)的圆的切线方程为x0x＋y0y＝r2.
(2)过圆(x－a)2＋(y－b)2＝r2上一点P(x0，y0)的圆的切线方程为(x0－a)(x－a)＋(y0－b)(y－b)＝r2.
(3)过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2.
5.切线长公式
记圆:；过圆外一点做圆的切线，切点为,利用勾股定理求；


【即学即练6】过点作圆的切线，则切线的方程为（  ）
A． B．
C． D．
【解析】因为，所以点在圆，又，所以切线的斜率为，所以切线方程为，整理得；
故选：C

【即学即练7】过点作圆的切线，则切线的方程为（   ）
A． B．
C．或 D．或
【解析】圆的圆心为原点，半径为1，
当切线的斜率不存在时，即直线的方程为，不与圆相切，
当切线的斜率存在时，设切线的方程为，即
所以，解得或
所以切线的方程为或
故选：C

【即学即练8】一条光线从点射出，经轴反射后与圆相切，则反射光线所在直线的斜率为（ ）
A．或 B．或 C．或 D．或
【解析】由光的反射原理知，反射光线的反向延长线必过点，设反射光线所在直线的斜率为，则反射光线所在直线方程为：，即：.
又因为光线与圆相切，所以，,
整理：，解得：，或,故选D．
知识点4 圆上点到直线的最大（小）距离
设圆心到直线的距离为，圆的半径为
①当直线与圆相离时，圆上的点到直线的最大距离为，最小距离为；
②当直线与圆相切时，圆上的点到直线的最大距离为，最小距离为；
③当直线与圆相交时，圆上的点到直线的最大距离为，最小距离为；
【即学即练9】圆上的点到直线的最大距离与最小距离的差是（   ）
A．36 B．18 C． D．
【解析】因为圆，即，
所以圆心坐标为，半径，
因为圆心到直线的距离，
所以直线与圆相离，
所以圆上的点到直线的最大距离与最小距离的差为，
故选：D.



考点一 直线与圆位置关系的判断
解题方略：
判断直线与圆位置关系的方法
(1)几何法：由圆心到直线的距离d与圆的半径r的大小关系判断．
(2)代数法：根据直线与圆的方程组成的方程组解的个数来判断．　
（一）判断直线与圆的位置关系
【例1-1】直线3x＋4y＋12＝0与圆C：(x－1)2＋(y－1)2＝9的位置关系是(　　)
A．相交并且直线过圆心　 B．相交但直线不过圆心
C．相切 D．相离
【解析】圆心C(1,1)到直线的距离d＝＝，圆C的半径r＝3，则d＞r，所以直线与圆相离．故选D

变式1：圆与直线的位置关系为（       ）
A．相切 B．相离 C．相交 D．无法确定
【解析】将圆的方程化为标准方程：，
得圆心坐标为，半径
则圆心到直线的距离
因为，所以圆与直线相离.
故选：B

变式2：直线与圆的位置关系为（       ）
A．相切 B．相交
C．相离 D．由的取值确定
【解析】因为圆心到直线的距离，即为圆的半径，所以可知直线与圆相切.
故选：A．

变式3：直线x－ky＋1＝0与圆x2＋y2＝1的位置关系是(　　)
A．相交　　　　　　　　　 B．相离
C．相交或相切 D．相切
【解析】直线x－ky＋1＝0恒过定点(－1,0)，而(－1,0)在圆上，故直线与圆相切或相交．故选C


变式4：已知直线，圆，则直线l与圆C的位置关系是（       ）
A．相离 B．相切 C．相交 D．不确定
【解析】直线，即，
由解得，因此，直线恒过定点，
又圆，即，显然点A在圆C外，
所以直线与圆C可能相离，可能相切，也可能相交，A，B，C都不正确，D正确.
故选：D


变式5：已知点(a，b)在圆C：x2＋y2＝r2(r≠0)的外部，则直线ax＋by＝r2与C的位置关系是(　　)
A．相切 B．相离
C．相交 D．不确定
【解析】由已知a2＋b2＞r2，且圆心到直线ax＋by＝r2的距离为d＝，则d＜r，故直线ax＋by＝r2与圆C的位置关系是相交.故选C.

变式6：直线绕原点按逆时针方向旋转后所得的直线l与圆的位置关系是（       ）
A．直线l过圆心 B．直线l与圆相交，但不过圆心
C．直线l与圆相切 D．直线l与圆无公共点
【解析】直线过原点，斜率为，倾斜角为，依题意，直线l的倾斜角为，斜率为，而l过原点，
因此，直线l的方程为：，又圆的圆心为，半径为，
于是得点到直线l的距离为，所以直线l与圆相切.
故选：C

（二）由直线与圆的位置关系求参数
【例1-2】求实数m的取值范围，使直线x－my＋3＝0与圆x2＋y2－6x＋5＝0分别满足：
(1)相交；(2)相切；(3)相离．
【解析】圆的方程化为标准式为(x－3)2＋y2＝4，
故圆心(3,0)到直线x－my＋3＝0的距离d＝，
圆的半径r＝2.
(1)若相交，则d 所以m∈(－∞，－2)∪(2，＋∞)．
(2)若相切，则d＝r，即＝2，
所以m＝±2.
(3)若相离，则d>r，即>2，
所以m∈(－2，2)．
变式1：直线与圆相切，则（       ）
A．3 B． C．或1 D．3或
【解析】圆的圆心坐标为，半径为
又直线与圆相切，
则，解之得或，
故选：D．

变式2：“直线++=0与圆相切”是“=1”的（     ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
【解析】依题意， ，即圆心是（1,0），半径为 ，
如果直线x+y+m=0是此圆的切线，则圆心到直线的距离为 ，
即 或-3，
所以“直线x+y+m=0与圆相切”不是m=1的充分条件；
如果m=1，则直线为x+y+1=0，圆心（1,0）到直线的距离为 ，即相切，
是必要条件；
故选：A.
变式3：已知直线与圆相交，则实数k的取值范围是（       ）
A． B．
C． D．
【解析】由题意，圆心到直线的距离，即，解得
故选：D

变式4：已知对任意的实数k，直线l：与圆C：有公共点，则实数t的取值范围为（       ）
A． B．
C． D．
【解析】由直线可化为，则直线l过定点，
因为直线l：与圆C：有公共点，
所以定点在圆C上或圆C内，可得，解得，
故选：B


【例1-3】已知圆上仅存在一个点到直线的距离为1，则实数a的值为（       ）
A．-2 B． C．-1 D．0
【解析】由圆的标准方程为，则圆心为，半径为且，
又到的距离，
所以要使圆上仅有一点到直线距离为1，只需且，则.
故选：D

变式1：若圆上到直线的距离等于的点恰有3个，则实数a的值为___________.
【解析】圆，即，
所以圆C的圆心坐标为，半径，
因为圆上到直线距离等于的点恰有3个，
设圆心到直线的距离为，则，
即，解得或，
故答案为：或.

【例1-4】若直线始终平分圆的周长，则的最小值为（       ）
A． B． C． D．
【解析】圆的圆心为，由题意可知，直线过圆心，则，
因为，则且，
因此，，
当且仅当时，等号成立，故的最小值为.
故选：A.


（三）由直线与圆的位置关系求距离最值
【例1-5】圆上的点到直线的最大距离与最小距离的差是（   ）
A．36 B．18 C． D．
【解析】因为圆，即，
所以圆心坐标为，半径，
因为圆心到直线的距离，
所以直线与圆相离，
所以圆上的点到直线的最大距离与最小距离的差为，
故选：D.

变式1：已知点是直线上的点，点是圆上的点，则的最小值是___________.
【解析】圆的圆心为，半径为1，
则圆心到直线的距离为
，
所以的最小值为，
故答案为：

变式2：已知，是圆上的两个动点，且，则，两点到直线的距离之和的取值范围是（       ）
A． B． C． D．
【解析】因为，所以为直角三角形，为斜边，
设线段的中点为，则，从而在圆上，
设，两点到直线的距离之和为，到直线的距离为，由题意得，
圆的圆心到直线的距离为，
所以，即，所以．
故选：D．


考点二 切线问题
解题方略：
1．过圆上一点(x0，y0)的圆的切线方程的求法
先求切点与圆心连线的斜率k，再由垂直关系得切线的斜率为－，由点斜式可得切线方程．如果斜率为零或不存在，则由图形可直接得切线方程y＝y0或x＝x0.
2．过圆外一点(x0，y0)的切线方程的求法
设切线方程为y－y0＝k(x－x0)，由圆心到直线的距离等于半径建立方程，可求得k，也就得切线方程．当用此法只求出一个方程时，另一个方程应为x＝x0，因为在上面解法中不包括斜率不存在的情况，而过圆外一点的切线有两条．一般不用联立方程组的方法求解．
3．求切线长(最值)的两种方法
(1)(代数法)直接利用勾股定理求出切线长，把切线长中的变量统一成一个，转化成函数求最值；
(2)(几何法)把切线长最值问题转化成圆心到直线的距离问题．　　

（一）求圆的切线方程
【例2-1】若点P(1,2)在以坐标原点为圆心的圆上，则该圆在点P处的切线方程为________．
【解析】设切线斜率为k，则由已知得： k·kOP＝－1.
∴k＝－.∴切线方程为x＋2y－5＝0.

变式1：过点作圆的切线，则切线方程为（       ）
A． B． C． D．或
【解析】由圆心为，半径为，
斜率存在时，设切线为，则，可得，
所以，即，
斜率不存在时，显然不与圆相切；
综上，切线方程为.
故选：C


【例2-2】过点A(－1,4)作圆(x－2)2＋(y－3)2＝1的切线l，求切线l的方程为________．
【解析】∵(－1－2)2＋(4－3)2＝10＞1，∴点A在圆外．
当直线l的斜率不存在时，l的方程是x＝－1，不满足题意．
设直线l的斜率为k，则切线l的方程为y－4＝k(x＋1)，
即kx－y＋4＋k＝0.
圆心(2,3)到切线l的距离为＝1，
解得k＝0或k＝－，
因此，所求直线l的方程y＝4或3x＋4y－13＝0.

【例2-3】以点(2，－1)为圆心，且与直线3x－4y＋5＝0相切的圆的方程为(　　)
A．(x－2)2＋(y＋1)2＝3 B．(x＋2)2＋(y－1)2＝3
C．(x＋2)2＋(y－1)2＝9 D．(x－2)2＋(y＋1)2＝9
【解析】圆心到直线3x－4y＋5＝0的距离d＝＝3，即圆的半径为3，所以所求圆的方程为
(x－2)2＋(y＋1)2＝9.故选D

变式1：已知圆C的圆心是直线x－y＋1＝0与x轴的交点，且圆C与直线x＋y＋3＝0相切，则圆C的方程为____________________．　
【解析】令y＝0得x＝－1，所以直线x－y＋1＝0与x轴的交点为(－1,0)．因为直线x＋y＋3＝0与圆相切，
所以圆心到直线的距离等于半径，
即r＝＝，
所以圆C的方程为(x＋1)2＋y2＝2.

变式2：【多选】与圆C：x2＋y2－4x＋2＝0相切，且在x，y轴上的截距相等的直线方程为(　　)
A．x＋y＝0 B．x－y＝0
C．x＝0 D．x＋y＝4
【解析】圆C的方程可化为(x－2)2＋y2＝2.可分为两种情况讨论：
(1)直线在x，y轴上的截距均为0，易知直线斜率必存在，设直线方程为y＝kx，则＝，解得k＝±1；
(2)直线在x，y轴上的截距均不为0，则可设直线方程为＋＝1(a≠0)，即x＋y－a＝0(a≠0)，则＝，解得a＝4(a＝0舍去)．故选A、B、D



（二）与切线长有关的问题
【例2-4】从圆外一点向圆引切线，则此切线的长为______．
【解析】将圆化为标准方程：，则圆心，半径1，
如图，设，，切线长．
故答案为：2


变式1：过原点O作圆x2＋y2－6x－8y＋20＝0的两条切线，设切点分别为P，Q，则线段PQ的长为________．
【解析】圆的方程化为标准方程为(x－3)2＋(y－4)2＝5，示意图如图所示．则圆心为O′(3,4)，r＝.切线长|OP|＝＝2.
∴|PQ|＝2·＝2×＝4.

变式2：由直线y＝x＋1上的一点向圆(x－3)2＋y2＝1引切线，则切线长的最小值为(　　)
A．1 B．2
C. D．3
【解析】因为切线长的最小值是当直线y＝x＋1上的点与圆心距离最小时取得，圆心(3,0)到直线y＝x＋1的距离为d＝＝2，圆的半径为1，所以切线长的最小值为＝＝，故选C.

变式3：已知圆：，为直线：上任一点，过点作圆的切线为切点)，则最小值是____．
【解析】圆：，圆心，半径，
设圆心到直线：的距离为，
故当圆心到直线上点的距离最小时，
即圆心到直线的距离，此时最小，
因为，所以，
故最小值是．
故答案为：.


变式4：点P是直线2x＋y＋10＝0上的动点，PA，PB与圆x2＋y2＝4分别相切于A，B两点，则四边形PAOB面积的最小值为________．
【解析】如图所示，因为S四边形PAOB＝2S△POA.又OA⊥AP，
所以S四边形PAOB＝2×|OA|·|PA|
＝2＝2.
为使四边形PAOB面积最小，当且仅当|OP|达到最小，即为点O到直线2x＋y＋10＝0的距离：|OP|min＝＝2.
故所求最小值为2＝8.
答案：8

变式5：已知圆，点M为直线上一个动点，过点M作圆C的两条切线，切点分别为A，B，则四边形周长的最小值为（       ）
A．8 B． C． D．
【解析】圆的圆心坐标为，半径为，
因为过点M作圆C的两条切线，切点分别为A，B，
所以有，，
因此有，
要想四边形周长最小，只需最小，即当时，
此时，此时，
即最小值为，
故选：A


变式6：已知圆：，点是直线上的动点，过作圆的两条切线，切点分别为，，则的最小值为（       ）
A． B． C． D．
【解析】圆：化为标准方程：，其圆心,半径.
过点P引圆C的两条切线,切点分别为点A、B,如图：

在△PAC中,有，即，变形可得：.
设，则.
所以当的值即x最小时，的值最大，此时最小.
而的最小值为点C到直线的距离，即，
所以.
故选：B


　　考点三 弦长问题
解题方略：
求弦长的两种方法
(1)由半径长r、弦心距d、弦长l的一半构成直角三角形，所以利用勾股定理d2＋2＝r2求解，这是常用解法．
(2)联立直线与圆的方程，消元得到关于x(或y)的一元二次方程，利用根与系数的关系得到两交点横坐标(或纵坐标)之间的关系，代入两点间距离公式求解．此解法很烦琐，一般不用．　　　　
【例3-1】在平面直角坐标系xOy中，直线x＋2y－3＝0被圆(x－2)2＋(y＋1)2＝4截得的弦长为________．
【解析】因为圆心(2，－1)到直线x＋2y－3＝0的距离d＝＝，所以直线x＋2y－3＝0被圆截得的弦长为2 ＝.

变式1：圆x2＋y2－4x＋4y＋6＝0截直线x－y－5＝0所得的弦长等于(　　)
A. B.
C．1 D．5
【解析】圆的方程可化为(x－2)2＋(y＋2)2＝2，则圆的半径r＝，圆心到直线的距离d＝＝，所以直线被圆截得的弦长为2＝2＝.故选A

变式2：若直线与圆的一个交点在x轴上，则l被C截得的弦长为______．
【解析】由题意得，直线与轴的交点为，则点在圆上，即，解得，则，圆心到的距离为，则l被C截得的弦长为.


变式3：若直线x－y＝2被圆(x－a)2＋y2＝4所截得的弦长为2，则实数a的值为(　　)
A．0或4 B．0或3
C．－2或6 D．－1或
【解析】由圆的方程，可知圆心坐标为(a,0)，半径r＝2.又直线被圆截得的弦长为2，所以圆心到直线的距离d＝ ＝.又d＝，所以|a－2|＝2，解得a＝4或a＝0.故选A.

变式4：一圆与y轴相切，圆心在直线x－3y＝0上，且直线y＝x截圆所得弦长为2，求此圆的方程．
【解析】因为圆与y轴相切，且圆心在直线x－3y＝0上，
故设圆的方程为(x－3b)2＋(y－b)2＝9b2.
又因为直线y＝x截圆得弦长为2，
则有2＋()2＝9b2，
解得b＝±1，故所求圆的方程为
(x－3)2＋(y－1)2＝9或(x＋3)2＋(y＋1)2＝9.

变式5：如果一条直线经过点M且被圆x2＋y2＝25所截得的弦长为8，求这条直线的方程．
【解析】圆x2＋y2＝25的半径长r为5，直线被圆所截得的弦长l＝8，于是弦心距d＝ ＝＝3.
因为圆心O(0,0)到直线x＝－3的距离恰为3，所以直线x＝－3是符合题意的一条直线．设直线y＋＝k(x＋3)也符合题意，即圆心到直线kx－y＋＝0的距离等于3，于是＝3，解得k＝－.
故直线的方程为3x＋4y＋15＝0.
综上可知，满足题意的直线有两条，对应的方程分别为x＝－3或3x＋4y＋15＝0.

变式6：已知直线与圆相交于，两点，试求弦的长及弦的垂直平分线方程．
【解析】圆的方程化为：，其圆心为，半径为．
因圆心到直线的距离，
故由勾股定理及垂径定理，得．
由于弦的垂直平分线经过圆心，其法向量为，故其方程为，即弦的垂直平分线的方程为：．

变式7：直线l与圆x2＋y2＋2x－4y＋a＝0(a＜3)相交于A，B两点，若弦AB的中点为C(－2,3)，则直线l的方程为(　　)
A．x－y＋5＝0 B．x＋y－1＝0
C．x－y－5＝0 D．x＋y－3＝0
【解析】由圆的一般方程可得圆心为M(－1,2)．由圆的性质易知M(－1,2)与C(－2,3)的连线与弦AB垂直，故有kAB×kMC＝－1⇒kAB＝1，故直线AB的方程为y－3＝x＋2，整理得x－y＋5＝0.

【例3-2】过点（-2，1）的直线中，被圆x2+y2-2x+4y=0截得的弦最长的直线的方程是（       ）
A．x+y+1=0 B．x+y-1=0 C．x-y+1=0 D．x-y-1=0
【解析】由题意得，圆的方程为，∴圆心坐标为．
∵直线被圆截得的弦长最大，∴直线过圆心，又直线过点（-2，1），
所以所求直线的方程为，
即．
故选：A．
变式1：过点(3,1)作圆(x－2)2＋(y－2)2＝4的弦，其中最短弦的长为________．
【解析】设点A(3,1)，易知圆心C(2,2)，半径r＝2.
当弦过点A(3,1)且与CA垂直时为最短弦，
|CA|＝＝.
∴半弦长＝＝＝.
∴最短弦的长为2.
答案：2

变式2：直线x＋7y－5＝0截圆x2＋y2＝1所得的两段弧长之差的绝对值是(　　)
A. B.
C．π D.
【解析】圆心到直线的距离d＝＝.又圆的半径r＝1，∴直线x＋7y－5＝0被圆x2＋y2＝1截得的弦长为，∴直线截圆所得的劣弧所对的圆心角为90°，∴劣弧是整个圆周的，∴直线截圆所得的两段弧长之差的绝对值为整个圆周长的一半，即×2πr＝π.故选C


考点四 直线与圆方程的应用
解题方略：
坐标方法解决平面几何问题的“三步曲”

【例4-1】某圆拱桥的水面跨度20 m，拱高4 m．现有一船，宽10 m，水面以上高3 m，这条船能否从桥下通过？
【解析】建立如图所示的坐标系，使圆心C在y轴上. 依题意，有A(－10，0)，B(10,0)，P(0,4)，D(－5，0)，E(5,0)．设这座圆拱桥的拱圆的方程是(x－a)2＋(y－b)2＝r2，于是有
解此方程组，得a＝0，b＝－10.5，r＝14.5.所以这座圆拱桥的拱圆的方程是x2＋(y＋10.5)2＝14.52(0≤y≤4)．把点D的横坐标x＝－5代入上式，得y≈3.1.由于船在水面以上高
3 m,3<3.1，所以该船可以从桥下通过．





变式1：苏州有很多圆拱的悬索拱桥（如寒山桥），经测得某圆拱索桥（如图）的跨度米，拱高米，在建造圆拱桥时每隔米需用一根支柱支撑，则与相距米的支柱的高度是（       ）米.（注意：≈）

A．6.48 B．5.48 C．4.48 D．3.48
【解析】以O为原点,以AB所在直线为x轴,以OP所在直线为y轴建立平面直角坐标系.

设圆心坐标为（0，a），则P(0,10),A(-50,0).
可设圆拱所在圆的方程为,由题意可得：
解得： .
所以所求圆的方程为.
将x=-30代入圆方程,得: ,
因为y>0,所以.
故选：A.


【例4-2】为了适应市场需要，某地准备建一个圆形生猪储备基地(如图)，它的附近有一条公路，从基地中心O处向东走1 km是储备基地的边界上的点A，接着向东再走7 km到达公路上的点B；从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D，修建一条由D通往公路BC的专用线DE，求DE的最短距离．
【解析】以O为坐标原点，OB，OC的直线分别为x轴和y轴，建立平面直角坐标系，则圆O的方程为x2＋y2＝1，因为点B(8,0)，C(0,8)，所以直线BC的方程为＋＝1，即x＋y＝8.
当点D选在与直线BC平行的直线(距BC较近的一条)与圆相切所成切点处时，DE为最短距离．此时DE的最小值为－1＝(4－1)km.


变式1：某考点配备的信号检测设备的监测范围是半径为100米的圆形区域，一名工作人员持手机以每分钟50米的速度从设备正东方向米的处出发，沿处西北方向走向位于设备正北方向的处，则这名工作人员被持续监测的时长为（       ）
A．1分钟 B．分钟
C．2分钟 D．分钟
【解析】以设备的位置为坐标原点，其正东方向为轴正方向，正北方向为轴正方向建立平面直角坐标系，如图所示，
则，，可得，圆．
记从处开始被监测，到处监测结束，
因为到的距离为米，
所以米，故监测时长为分钟．
故选：C.

变式2：如图，已知一艘海监船O上配有雷达，其监测范围是半径为的圆形区域，一艘外籍轮船从位于海监船正东的A处出发，径直驶向位于海监船正北的B处岛屿，速度是，问：这艘外籍轮船能否被海监船监测到？若能，持续时间为多长？

【解析】如图，以为原点，东西方向为轴建立直角坐标系,

则，，圆方程，
直线方程：，即，
设到距离为，则，
所以外籍轮船能被海监船检测到，
设监测时间为，则（小时），
答：外籍轮船能被海监船检测到，时间是0.5小时


题组A 基础过关练
1．当圆截直线所得的弦最长时，则m的值为（       ）
A． B．-1 C．1 D．
【解析】要使直线与圆所得弦最长，则直线必过圆心，
所以，可得.
故选：C
2．圆x2＋y2－2x＋4y＝0与直线2x+y+1＝0的位置关系为（　 　）
A．相离 B．相切 C．相交 D．以上都有可能
【解析】圆x2＋y2－2x＋4y＝0的圆心坐标为，半径
圆心到直线2x+y+1＝0的距离
由，可得圆与直线的位置关系为相交.
故选：C
3．直线与圆相切，则实数m等于（       ）
A．2 B． C．或 D．
【解析】因为直线与圆相切，故，即，故
故选：D
4．已知点是圆内一点，直线l是以M为中点的弦所在的直线，直线m的方程为，那么（       ）
A．且m与圆C相切 B．且m与圆C相切
C．且m与圆C相离 D．且m与圆C相离
【解析】由点是圆内一点得．
所以圆心到直线的距离为．
故直线m与圆C相离．
另一方面，直线的斜率为，而直线l以M为中点，故直线．
又直线m的斜率也是2，所以，所以.
故选：C．
5．不论k为何值，直线都与圆相交，则该圆的方程可以是（　　）
A． B．
C． D．
【解析】，   ，∴直线恒过点P（—4，1） ，
对于A，圆心为（2，-1），半径为5，P到圆心的距离为：     ，
即P点不在该圆内；
对于B，圆心为（-1，-2），半径为5，P到圆心的距离为 ，
故点P在该圆内；
对于C，圆心为（3，-4），半径为5，P点到圆心的距离为 ，
故点P不在该圆内；
对于D，圆心为（-1，-3），半径为5，点P到圆心的距离为 ，
点P该在圆上，可能相切也可能相交；
故选：B.
6．如图，斜率为的直线与x轴交于点D，与y轴交于点A，与圆相切于点B，则_______.

【解析】由题意知，，，则，则，，
则，，则.
故答案为：.
7．过点（7，-2）且与直线相切的半径最小的圆方程是（       ）
A． B．
C． D．
【解析】过点作直线的垂线，垂足为，
则以为直径的圆为直线相切的半径最小的圆，
其中，设，
则，解得：，
故的中点，即圆心为，即，
故该圆为
故选：B
8．已知直线与x轴和y轴分别交于A、B两点，动点P在以点A为圆心，2为半径的圆上，当 最大时，△APB的面积为（       ）
A． B．1 C．2 D．
【解析】由已知，圆A的方程为，当最大时，
此时直线PB是圆的切线，即直线PB的方程为：或，
当直线PA的方程为时，△APB的面积为，
当直线PA的方程为时，△APB的面积为，
故选：C．
9．直线与圆的位置关系是（       ）
A．相切 B．相离 C．相交 D．不确定
【解析】因为，所以圆心到直线的距离，所以直线与圆相离.
故选：B.
10．已知直线与圆有两个不同的交点，则实数的取值范围是（       ）
A． B． C． D．
【解析】因为直线与圆有两个不同的交点，
所以圆心到直线的距离，即，解得，
所以实数的取值范围是，
故选：B.
11．设点，若直线关于对称的直线与圆有公共点，则a的取值范围是________．
【解析】关于对称的点的坐标为，在直线上，
所以所在直线即为直线，所以直线为，即；
圆，圆心，半径，
依题意圆心到直线的距离，
即，解得，即；
故答案为：
12．若圆上至少有三个不同点到直线的距离为，则的取值范围__．
【解析】由圆的标准方程，
可得圆心坐标为，半径为，
圆上至少有三个不同的点到直线的距离为，
则圆心到直线的距离应不大于等于，即，
整理得，解得，
即实数的取值范围是.
故答案为：.
13．直线分别与x轴，y轴交于两点，点在圆，则面积的取值范围是（       ）
A． B．
C． D．
【解析】因为，所以.
圆的标准方程，圆心，
圆心到直线的距离为，
所以，点到直线的距离的取值范围为：，
所以.
故选:C.
14．如图，P为圆O：x2+y2＝4外一动点，过点P作圆O的切线PA，PB，切点分别为A，B，∠APB＝120°，直线OP与AB相交于点Q，点M（3，），则|MQ|的最小值为（       ）


A． B．2 C． D．
【解析】过点P作圆O的切线PA，PB，切点分别为A，B，∠APB＝120°，
由圆与切线的平面几何性质知，∠APO＝60°，又|OA|＝2，则可得|OP|＝
在直角中，，由得，
∴Q点的轨迹是以O为圆心，为半径的圆，方程为x2+y2＝3；
|MQ|的最小值即为|OM|﹣r＝﹣＝．
故选：A．
15．已知圆圆心为原点，且与直线相切，直线l过点．
(1)求圆的标准方程；
(2)若直线l被圆所截得的弦长为，求直线l的方程．
【解析】(1)设圆的半径为，则，故圆的标准方程为；
(2)设圆心到直线到的距离为，则，解得；当直线l斜率不存在时，易得，此时圆心到的距离，符合题意；
当直线l斜率存在时，设，即，则，解得，即，
故直线l的方程为或.
16．已知圆.
(1)过点作圆C的切线l，求切线l的方程；
(2)设过点的直线m与圆C交于AB两点，若点A、B分圆周得两段弧长之比为1：2，求直线m得方程.
【解析】(1)由可得，
即圆心为，半径，
显然当直线斜率不存在时，是圆的切线，
当直线斜率存在时，设直线为，即，
由圆心到直线的距离，解得，
故切线为或.
(2)因为点A、B分圆周得两段弧长之比为1：2，故,
所以，故圆心到直线的距离，
直线斜率不存在时，由知，不符合题意，
当直线斜率存在时，设直线方程为，
则圆心到直线的距离，解得，
故直线方程为或.

17．已知直线方程mx－y－m－1＝0，圆的方程x2＋y2－4x－2y＋1＝0.当m为何值时，圆与直线：
(1)有两个公共点；
(2)只有一个公共点；
(3)没有公共点．
【解析】法一：将直线mx－y－m－1＝0代入圆的方程化简整理得，
(1＋m2)x2－2(m2＋2m＋2)x＋m2＋4m＋4＝0.
则Δ＝4m(3m＋4)．
(1)当Δ>0，即m>0或m<－时，直线与圆相交，即直线与圆有两个公共点；
(2)当Δ＝0，即m＝0或m＝－时，直线与圆相切，即直线与圆只有一个公共点；
(3)当Δ<0，即－ 法二：已知圆的方程可化为(x－2)2＋(y－1)2＝4，
即圆心为C(2,1)，半径r＝2.
圆心C(2,1)到直线mx－y－m－1＝0的距离
d＝＝ .
(1)当d<2，即m>0或m<－时，直线与圆相交，即直线与圆有两个公共点；
(2)当d＝2，即m＝0或m＝－时，直线与圆相切，即直线与圆只有一个公共点；
(3)当d>2，即－ 18．求过直线和圆的交点，并且面积最小的圆的方程．
【解析】由已知条件，所求圆一定是以直线被圆截得的弦为直径的圆，
由方程组，解得直径的两端点分别为，，线段的中点为即所求圆的圆心，，则，
所求圆的方程为.


题组B 能力提升练

19．一辆卡车宽1.6米，要经过一个半径为3.6米的半圆形隧道，则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过(　　)
A．1.4米 B．3.5米
C．3.6米 D．2米
【解析】建立如图所示的平面直角坐标系．如图设蓬顶距地面高度为h，则A(0.8，h－3.6)所在圆的方程为： x2＋(y＋3.6)2＝3.62，把A(0.8，h－3.6)代入得0.82＋h2＝3.62.
∴h＝4≈3.5(米)．故选B



20．已知圆，圆，若圆M上存在点P，过点P作圆O的两条切线，切点分别为A，B，使得，则实数的取值范围是（       ）
A． B． C． D．
【解析】由题可知圆O 的半径为，圆M上存在点P，过点P作圆 O 的两条切线，
切点分别为A，B，使得，则，
在中，，
所以点 在圆上，
由于点 P 也在圆 M 上，故两圆有公共点.
又圆 M 的半径等于1，圆心坐标，
，
∴，
∴.
故选：D.
21．圆与直线的位置关系为（       ）
A．相切 B．相离 C．相交 D．无法确定
【解析】直线可化为，所以恒过定点.
把代入，有：，
所以在圆内，所以圆与直线的位置关系为相交.
故选：C
22．若“直线与圆相交”，“”，则是的（       ）
A．必要而不充分条件 B．充分而不必要条件
C．充要条件 D．既不充分也不必要条件
【解析】直线与圆相交，可得1，解得，
且，
∴“直线与圆相交”是“”的充分而不必要条件.
故选：B.
23．若方程有两个不等的实根，则实数b的取值范围为（       ）
A． B． C． D．
【解析】由得，
所以直线与半圆有个公共点，
作出直线与半圆的图形，如图：

当直线经过点时，，
当直线与圆相切时，，解得或（舍），
由图可知，当直线与曲线有个公共点时，，
故选：B.
24．已知直线与圆相交于两点，当变化时，△的面积的最大值为（       ）
A． B． C． D．
【解析】因为直线直线恒过点在圆内，所以直线与圆相交，
圆的圆心，所以△的面积的最大值为：
.

故选：C.
25．已知圆C:与直线l:，若直线l与圆C交于A，B两点，且∠AOB=90°（O为坐标原点），则b=____，|AB|=____.
【解析】，得，
联立得
有
∠AOB=90°，故
代入解得
圆心到直线的距离，
故答案为：，4
26．在平面直角坐标系中，光线过点，经轴反射后与圆：有交点
(1)当反射后光线经过圆心，求光线的方程；
(2)当反射后光线与圆相切，求光线的方程．
【解析】(1)点关于轴对称的点为，由光线的折射性质，反射光线经过圆心，所以，
易知，所以，
所以光线的方程为.
(2)设经过的直线方程为由于折射光线与圆相切，
所以圆心到直线的距离等于半径，即,
化简得：,
解得或,
所光线的方程为或.
27．已知是圆外一点．
(1)过M作圆O的切线l，求切线l的方程；
(2)过M任意作一条割线，交圆O于AB两点，求弦AB的中点C的轨迹方程．
【解析】(1)圆的圆心是原点，半径是2，
过且斜率不存在的直线是与圆相切，
当过的切线斜率存在时，设切线方程为，即，
由，解得，
所以切线方程为，即，
所以切线方程为和；
(2)是中点，则，即，所以点在以为直径的圆上，
中点坐标为，，
所以以为直径的圆方程为，即，
所以点轨迹方程为（在圆内部）．

题组C 培优拔尖练
28．已知圆，点M为直线上一个动点，过点M作圆C的两条切线，切点分别为A，B，则当四边形周长取最小值时，四边形的外接圆方程为（       ）
A． B．
C． D．
【解析】圆的圆心，半径，点C到直线l的距离，
依题意，，四边形周长，
当且仅当时取“=”，此时直线，由得点，
四边形的外接圆圆心为线段中点，半径，方程为.
故选：D
29．已知，过点作圆（为参数，且）的两条切线分别切圆于点、，则的最大值为（       ）
A． B． C． D．
【解析】圆心，半径为，圆心在直线上运动，
设，则，由圆的几何性质可知，
所以，，
当直线与直线垂直时，取最小值，则取最小值，
且，则，则，
由双勾函数的单调性可知，函数在上为增函数，且，
故函数在上为减函数，
故当时，取得最大值.
故选：C.
30．已知：，直线：，为直线上的动点，过点作的切线，，切点为，，当四边形的面积取最小值时，直线AB的方程为 ____．
【解析】：的标准方程为，
则圆心，半径．
因为四边形的面积，
要使四边形面积最小，则需最小，此时与直线垂直，
直线的方程为，即，
联立，解得．则,
则以为直径的圆的方程为，
与的方程作差可得直线的方程为．
故答案为：.
31．已知圆，点P是直线上的动点，过P作圆的两条切线，切点分别为A，B，则的最小值为______．
【解析】圆，即，
由于PA，PB分别切圆C于点A，B，则，
，，所以，
因为，所以，
又，所以，
所以，即，
所以最短时，最短，
点C到直线的距离即为的最小值，
所以，所以的最小值为

故答案为：
32．已知直线与圆交于不同的两点，，点，则的最大值为______．
【解析】由，得．
设，，则，，
因为，所以
．
令，则，，
所以
，
当且仅当时等号成立．
所以的最大值为．
故答案为：.
33．已知圆M的方程为．
(1)求过点与圆M相切的直线l的方程；
(2)过点作两条相异直线分别与圆M相交于A，B两点，若直线的斜率分别为，且，试判断直线的斜率是否为定值，并说明理由．
【解析】(1)显然当l的斜率不存在时，不符合题意；设，直线与圆相切，
由圆心到直线l距离，解得或．
当时，直线l的方程为，当时，直线l的方程为，
所以直线l的方程为或．
(2)由题意可设
由可得，
设，则，所以，
，同理，
因为，所以，
所以为定值．
34．已知直线与圆相交于，不同两点.
(1)若，求的值；
(2)设是圆上一动点，为坐标原点，若，求点到直线的最大距离．
【解析】(1)可整理为，
圆心为，半径为1，直线的l一般式为，
又∵直线与圆交于两点，∴，
解得，
∵，∴或2.
(2)设，，
将代入方程，整理得，
∴，，
，
由题设可得，解得，由（1）知，
所以直线的方程为，
可知圆心在直线上，∴到直线的最大距离即为半径为1．
35．已知直线：与轴相交于点，过直线上的动点作圆的两条切线，切点分别为，两点，记是的中点，则的最小值为__________．
【解析】由题意设点，，，
因为，是圆的切线，所以，，
所以在以为直径的圆上，其圆的方程为:
，又在圆上，
将两个圆的方程作差得直线的方程为：，
即，所以直线恒过定点，
又因为，，，，四点共线，所以，
即在以为直径的圆上，
其圆心为，半径为，如图所示:

所以，
所以的最小值为.
故答案为：.

36．如图，已知以点A(－1,2)为圆心的圆与直线l1：x＋2y＋7＝0相切．过点B(－2,0)的动直线l与圆A交于M，N两点．
(1)求圆A的方程；
(2)当|MN|＝2时，求直线l的方程．
【解析】(1)设圆A的半径为r.∵圆A与直线l1：x＋2y＋7＝0相切，∴r＝＝2.
∴圆A的方程为(x＋1)2＋(y－2)2＝20.
(2)①当直线l与x轴垂直时，直线l的方程为x＝－2，
易得|MN|＝2，符合题意；
②当直线l与x轴不垂直时，
设直线l的方程为y＝k(x＋2)，即kx－y＋2k＝0.
取MN的中点Q，连接AQ，则AQ⊥MN.
∵|MN|＝2，∴|AQ|＝＝1，
∴＝1，得k＝，
∴直线l的方程为3x－4y＋6＝0.
综上，直线l的方程为x＝－2或3x－4y＋6＝0.

37．已知直线l：4x＋3y＋10＝0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方．
(1)求圆C的方程；
(2)过点M(1,0)的直线与圆C交于A，B两点(A在x轴上方)，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．
【解析】(1)设圆心C(a,0)，则＝2⇒a＝0或a＝－5(舍)．所以圆C：x2＋y2＝4.
(2)当直线AB⊥x轴时，x轴平分∠ANB.
当直线AB的斜率存在时，设直线AB的方程为y＝k(x－1)，N(t,0)，A(x1，y1)，B(x2，y2)，
由得，(k2＋1)x2－2k2x＋k2－4＝0，
所以x1＋x2＝，x1x2＝.若x轴平分∠ANB，则kAN＝－kBN⇒＋＝0⇒＋＝0⇒2x1x2－(t＋1)(x1＋x2)＋2t＝0⇒－＋2t＝0⇒t＝4，
所以当点N为(4,0)时，能使得∠ANM＝∠BNM总成立．