

高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体第二课时教案
展开9.2.1-2总体取值规律的估计、总体百分位数的估计
【教学目标】
1.理解并掌握统计图表的画法及应用.
2.结合问题1和问题2,学会用样本估计总体的取值规律,估计总体的百分位数.
【学习过程】
新知学习:
问题1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作。
阅读课本192-195页解决提出的问题1,并掌握绘制频率分布表,绘制频率分布直方图的步骤:
1、绘制步骤:
①求_______ ,即一组数据中的最大值与最小值的差.
②决定_____ 与_______ .一般数据的个数越多,所分组数越_____.当样本容量不超过100时,常分成5~12组.为方便起见,一般取 _______ 组距,并且组距应力求“_________”.
③将数据_________ .
④列________表.一般分四列:分组、频数累计、频数、频率.其中计算各小组的频率,第i组的频率是__________. 频数合计应是样本容量,频率合计是1.
⑤画频率分布直方图.其中横轴表示分组,纵轴表示__________ 实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的_________程度,小长方形的面积=组距×=频率.各小长方形的面积和等于1.
2、.除了频率分布的直方图,还有没有类似的统计数据处理方法?它们表示数据上有什么特点?请阅读课本198页到200页,学习例1,会用条形图,扇形图,折线图对数据作出直观描述。
统计图表 | 主要应用 |
扇形图 | 直观描述各类数据占总数的比例 |
条形图和直方图 | 直观描述不同类别或分组数据的频数和频率 |
折线图 | 描述数据随时间的变化趋势 |
题型一:统计图表的运用:
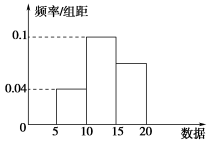 1.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,60)内的汽车有( )
1.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,60)内的汽车有( )
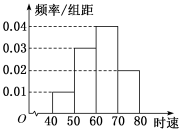
(1题图) (2题图)
A.30辆 B.40辆 C.60辆 D.80辆
2.如图所示是一容量为100的样本的频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )
A.20 B.30 C.40 D.50
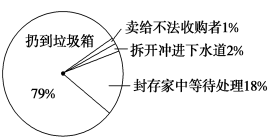
3.把过期的药品随意丢弃,会造成对土壤和水体的污染,危害人们的健康.如何处理过期药品,有关机构随机对若干家庭进行调查,调查结果如图,其中对过期药品处理不正确的家庭达到( )
4.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
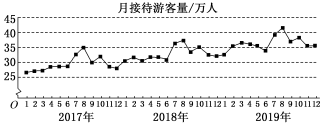
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
A.79% B.80% C.18% D.82%
问题2: 如果该市政府希望使80%的居民用户生活用水费支出不受影响,根据9.2.1节中100户居民用户的月均用水量数据,你能给市政府提出确定居民用户月均用水量标准的建议吗?
阅读课本201-202页解决提出的问题2,掌握第p百分位数的定义和求法;学习202页例2,会求一组数据的第p百分位数;学习例3,学会根据频率分布表和频率分布直方图求第p百分位数。
1、第p百分位数的定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
2、计算一组n个数据的第p百分位数的步骤
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
注意:如第50百分位数,也叫50%分位数,也就是熟知的中位数,可通过第50百分位数来理解第p百分位数。又如:25%,50%,75%这三个分位数把一组数据由小到大排列后的数据分成四等份,因此称为四分位数.
题型二:求第p百分位数
1.高一(1)班数学兴趣小组8名同学的数学竞赛成绩(单位:分)分别为:80,68,90,70,88,96,89,98,则该数学成绩的15%和50%分位数分别为________.
2.下列一组数据的第25百分位数是( )
2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6
A.3.2 B.3.0 C.4.4 D.2.5
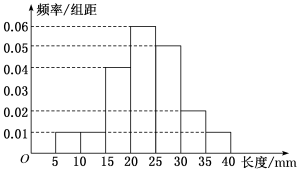
3.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.估计棉花纤维的长度的样本数据的80%分位数是( )
A.28 mm B.28.5 mm C.29 mm D.29.5 mm
4.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
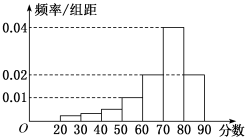 (1)估计总体400名学生中分数小于70的人数;
(1)估计总体400名学生中分数小于70的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把百分之15的学生划定为不及格,利用(2)中的数据,确定本次测试的及格分数线,低于及格分数线的学生需要补考.
高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体精品教案及反思: 这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体精品教案及反思,共12页。
高中数学第九章 统计9.2 用样本估计总体教学设计: 这是一份高中数学第九章 统计9.2 用样本估计总体教学设计,共10页。教案主要包含了问题导入,知识探究,课堂巩固,课堂小结,布置作业等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体教案: 这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体教案,共7页。教案主要包含了教学目标,教学重难点,教学过程,课外作业等内容,欢迎下载使用。













