数学八年级上册11.1 平面上的点坐标教案配套ppt课件

这是一份数学八年级上册11.1 平面上的点坐标教案配套ppt课件，共19页。PPT课件主要包含了旧知回顾，探究新知，例题与练习，它的面积是，解设OC＝m，OC＝2，－2－3，随堂练习等内容，欢迎下载使用。

利用点的坐标描点及计算图形的面积
思考：如何利用点的坐标描点，并计算图形面积？
阅读教材P5～P7的内容，回答下列问题：
在平面直角坐标系内描点，并将各点用 依次连接起来，就可以得到一个 图形．求图形的面积时，通常采取向 轴或 轴作垂线，将不规则的几何图形割补成我们常见的几何图形，然后用学过的面积公式计算．
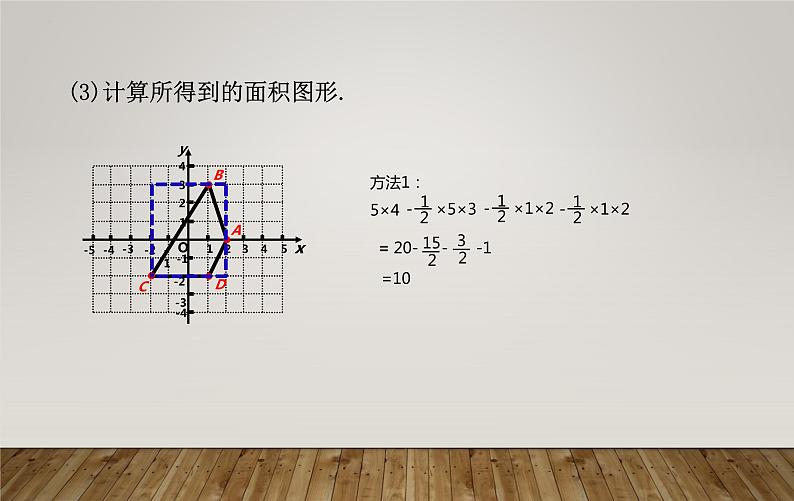
(1)如图，在平面直角坐标系中描绘出下列各点:
(2)按次序A→B →C →D →A将所描绘出的点用线段连接起来，看看得到的是什么图形？
解：(2)按次序A→B →C →D →A将所描的点用线段连接，得到的是四边形.
A(2,0)，B(1,3)，C(-2,-2) ，D(1,-2).
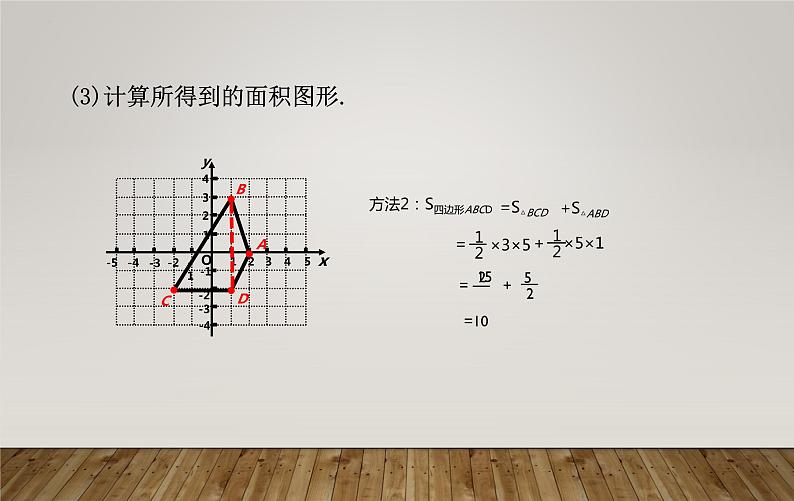
(3)计算所得到的面积图形.
在平面直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来得到一个封闭图形，说说你得到的是什么图形，并计算它们的面积.
A(-1,2) , B(-2,-1) , C(2,-1) , D(3,2)
解：得到的是一个平行四边形，
1.图中星形是由哪些点按顺序用线段连成的？说出这些点的坐标.
A（0,6），B（2,4），C（4,4），D（4,2），E（6,0），F（4,-2），G（4,-4），H（2,-4）I（0,-6），J（-2,-4），K（-4,-4），L（-4,-2），M（-6,0），N（-4,2），O（-4,4），P（-2,4）.
解：分别过A点和B点引x轴的垂线，垂足分别为D和C.
如图，已知△OBA的三个顶点坐标分别为O(0，0)、A(－5，－7)、B(4，－3)，则△OBA的面积是多少？
点A(3，0)，点B(－2，0)，点C在y轴上，如果△ABC的面积为5，求点C的坐标．
∴C(0，2)或(0，－2)．
建立坐标系求图形中点的坐标
如图，正方形ABCD的边长为4，请建立一个平面直角坐标系，并写出正方形的四个顶点A，B，C，D在这个平面直角坐标系的坐标.
解: 如图，以顶点A为原点，AB所在的直线为x轴，AD所在的直线为y轴建立平面直角坐标系.
A（0,0），B（4,0）， C（4,4），D（0,4）.
阅读教材P7的内容，回答下列问题：
思考：如何建立平面直角坐标系，不同的坐标系中图形顶点坐标会变化吗？
答：以不同的顶点为原点，就可建立不同的坐标系，在不同的直角坐标系中，同一图形的顶点坐标也不同，应根据具体情况建立适当的直角坐标系．
如图是某市市区四个旅游景点示意图(图中每个小正方形的边长为1个单位长度)，请以某景点为原点，建立平面直角坐标系，并用坐标表示下列景点的位置：
(1)动物园 ，烈士陵园 ；
解：如果以金凤广场为原点，则坐标图如图所示，动物园的位置为(1，2)，烈士陵园的位置为(－2，－3)；
(2)求由开心岛、金凤广场、烈士陵园三点构成的三角形的面积．
１．已知A(1,4), B(-4,0),C(2,0). △ABC的面积是＿＿＿．2.若BC的坐标不变, △ABC的面积为6,点A的横坐标为-1,那么点A的坐标为 ．
(-1,2)或(-1,-2)
3.已知点A、B在平面直角坐标系中的位置如图所示，求三角形AOB的面积.
解：由图可知A(-1,2) ， B(3,-2) 得C(1,0) ， D(3,0) ，E(-1,0). 由点的坐标可知 AE=2 ，OC=1，BD=2 . S△ AOB = S△AOC+S△BOC = 　OC·AE+　 OC·BD 　　 = 　×1×2+　×1×2=2.
4、如图，已知点A(2，－1)，B(4，3)，C(1，2)，求△ABC的面积．
解：如图，作辅助线.∵A(2，－1)，B(4，3)，C(1，2)，∴BD＝3，CD＝1，CE＝3，AE＝1， AF＝2，BF＝4，∴S△ABC＝S长方形BDEF－S△BDC－S△CEA－S△BFA ＝BD·DE－ DC·DB－ CE·AE－ AF·BF ＝12－1.5－1.5－4 ＝5.