





所属成套资源:北师大版数学九年级上学期PPT课件整套
北师大版九年级上册1 反比例函数评优课课件ppt
展开
这是一份北师大版九年级上册1 反比例函数评优课课件ppt,共22页。PPT课件主要包含了学习目标,xy15或,导入新课,讲授新课,概念归纳,是k3,不是它是正比例函数,是k1,归纳总结,典例精析等内容,欢迎下载使用。
1.理解并掌握反比例函数的意义及概念.(重点)2.会判断一个函数是否是反比例函数.(重点)3.会求反比例函数的表达式.(难点)
当面积 S=15m2 时,长y(m)与宽x(m)的关系是:
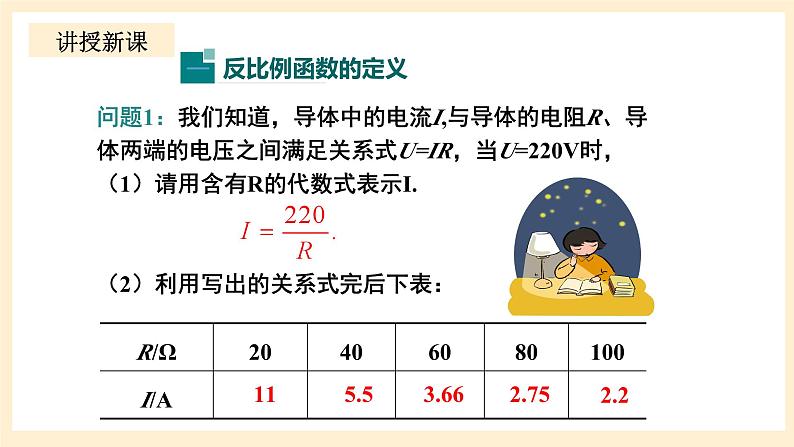
问题1:我们知道,导体中的电流I,与导体的电阻R、导体两端的电压之间满足关系式U=IR,当U=220V时,(1)请用含有R的代数式表示I.(2)利用写出的关系式完后下表:
当R 越来越大时,I 怎样变化?当R 越来越小呢?(3)变量I 是R的函数吗?为什么?
I 随着R的增大而变小,随着R 的减小而变大.
问题2:京沪高速公路全长约为1318km,汽车沿京沪高速公路从上海驶往北京,汽车行完全程所需的时间t (h)与行驶的平均速度v( km /h)之间有怎样的关系?变量t是v的函数吗?为什么?
变量t 与v之间的关系可以表示成:
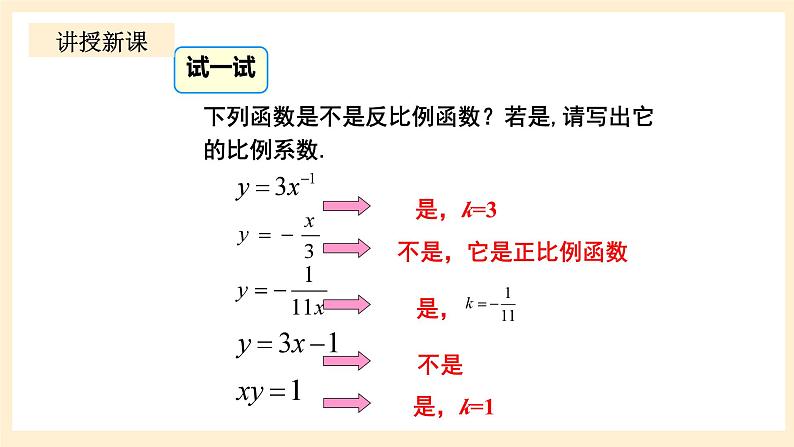
一般地,如果两个变量y与x的关系可以表示成
其中x是自变量不能为0,常数k(k≠0)称为反比例函数的反比例系数.
反比例函数的三种表达方式:(注意:k≠0)
例1:若函数 是反比例函数,求k的值,并写出该反比例函数的解析式.
解:由题意得4-k2=0,且k-2≠0 ,解得k=-2.因此该反比例函数的解析式为
1.已知函数 是反比例函数,则k必须满足 .
2.当m 时, 是反比例函数.
例2:已知y是x的反比例函数,当x=-4时,y=3.(1)写出y与x之间的函数表达式;(2)当x=-2时,求y的值;(3)当y=12时,求x的值.
解:(1)设 ∵当x=-4时,y=3, ∴3= ,解得k=-12. 因此,y和x之间的函数表达式为y=- ;
(2)把x=-2代入y=- ,得y=-=6;(3)把y=12 代入y=- ,得12=- ,x=-1.
(1)求反比例函数表达式时常用待定系数法,先设其表达式为y=kx(k≠0),然后再求出k值;(2)当反比例函数的表达式y=kx(k≠0)确定以后,已知x(或y)的值,将其代入表达式中即可求得相应的y(或x)的值.
例3:已知y与x-1成反比例,当x = 2时,y = 4.(1)用含有x的代数式表示y;(2)当x=3时,求y的值.
解:(1)设y = (k≠0), 因为当 x=2时,y=4,所以4= , 解得 k = 4. 所以y 与 x 的函数表达式是y= ; (2)当x = 3时,y= =2.
2.小明家离学校1000 m,每天他往返于两地之间,有时步行,有时骑车.假设小明每天上学时的平均速度为v(m/min),所用的时间为t(min). (1)求变量v和t之间的函数表达式; (2)星期二他步行上学用了25 min,星期三他骑自行车上学用了8 min,那么他星期三上学时的平均速度比星期二快多少呢?
解:(1) (t>0). (2)当t=25时, ; 当t=8时, , 125-40=85(m/min).答:小明星期三上学时的平均速度比星期二快85 m/min.
用待定系数法求反比例函数
反比例函数: (k≠0)
相关课件
这是一份初中数学北师大版九年级上册1 反比例函数教学ppt课件,共14页。PPT课件主要包含了学习目标,情境导入,探究新知,典例精析,课堂练习,反比例函数的概念,课堂小结,反比例函数的形式等内容,欢迎下载使用。
这是一份北师大版九年级上册1 反比例函数优秀ppt课件,文件包含61反比例函数教学课件pptx、第六章反比例函数61反比例函数教案内含练习docx等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
这是一份北师大版九年级上册3 反比例函数的应用试讲课课件ppt,共34页。PPT课件主要包含了学习目标,导入新课,增减性,双曲线,三象限,y随x的增大而增大,四象限,y随x的增大而减小,讲授新课,变形得等内容,欢迎下载使用。










