


第十一章 三角形 单元测试 2022-2023学年人教版数学八年级下上册
展开
这是一份第十一章 三角形 单元测试 2022-2023学年人教版数学八年级下上册,共7页。
![]() 第十一章 三角形 单元测试 2022-2023学年人教版数学八年级上册一、单选题1.下列语句正确的是( )A.三角形的角平分线、中线和高都在三角形内B.直角三角形的高只有一条C.三角形的高至少有一条在三角形内D.钝角三角形的三条高都在三角形外2.正多边形的每一个外角都等于45°,则这个多边形的边数是( ) A.6 B.7 C.8 D.93.已知三角形的两边长分别是4、7,则第三边长a的取值范围是( ) A.3<a<11 B.3≤a≤11 C.a>3 D.a<114.如图,∠1+∠2+∠3+∠4+∠5+∠6=( )
第十一章 三角形 单元测试 2022-2023学年人教版数学八年级上册一、单选题1.下列语句正确的是( )A.三角形的角平分线、中线和高都在三角形内B.直角三角形的高只有一条C.三角形的高至少有一条在三角形内D.钝角三角形的三条高都在三角形外2.正多边形的每一个外角都等于45°,则这个多边形的边数是( ) A.6 B.7 C.8 D.93.已知三角形的两边长分别是4、7,则第三边长a的取值范围是( ) A.3<a<11 B.3≤a≤11 C.a>3 D.a<114.如图,∠1+∠2+∠3+∠4+∠5+∠6=( ) 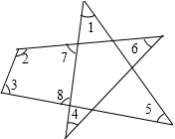 A.180° B.270° C.360° D.不能确定5.如图, 在
A.180° B.270° C.360° D.不能确定5.如图, 在 ![]() 中,
中, ![]() ,点D是B C延长线上一点, 且
,点D是B C延长线上一点, 且 ![]() , 已知
, 已知 ![]() , 则
, 则 ![]() 的面积为( )
的面积为( ) 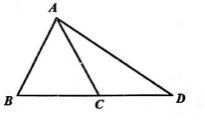 A.7 B.14 C.21 D.286.如图,D,E是△ABC中BC边上的点,且BD=DE=EC,那么( )
A.7 B.14 C.21 D.286.如图,D,E是△ABC中BC边上的点,且BD=DE=EC,那么( ) 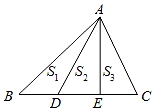 A.S1<S2<S3 B.S1>S2>S3 C.S1=S2=S3 D.S2<S1<S37.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.S1<S2<S3 B.S1>S2>S3 C.S1=S2=S3 D.S2<S1<S37.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( ) 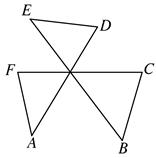 A.180° B.270° C.360° D.720°8.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A.180° B.270° C.360° D.720°8.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( ) 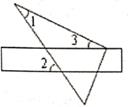 A.20° B.30° C.50° D.80°二、填空题9.在△ABC中,∠A=50°,∠B,∠C的角平分线相交于点O,则∠BOC的度数是 .10.正多边形的每一个内角比相邻的外角大90°,则这个多边形的边数是 11.已知
A.20° B.30° C.50° D.80°二、填空题9.在△ABC中,∠A=50°,∠B,∠C的角平分线相交于点O,则∠BOC的度数是 .10.正多边形的每一个内角比相邻的外角大90°,则这个多边形的边数是 11.已知![]() 的三个内角的度数之比
的三个内角的度数之比![]() :
:![]() :
:![]() :
:![]() :
:![]() ,则
,则![]() 度,
度,![]() 度.12.如图,已知
度.12.如图,已知 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() .
. 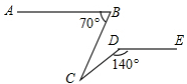 13.如图,
13.如图, ![]() 中,点
中,点 ![]() 在
在 ![]() 上且
上且 ![]() ,点
,点 ![]() 是
是 ![]() 中点,已知
中点,已知 ![]() 面积为2,那么
面积为2,那么 ![]() 的面积为 .
的面积为 . 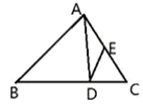 14.如图所示,在△ABC中,∠A=66°,点I是三条角平分线的交点,则∠BIC的大小为
14.如图所示,在△ABC中,∠A=66°,点I是三条角平分线的交点,则∠BIC的大小为  三、解答题15.将长度为24的一根铝丝折成各边均为正整数的三角形,这个三角形的三边分别记为a、b、c,且a≤b≤c,请写出满足题意的a、b、c. 16.已知:如图,△ABC的两条高线BD、CE相交于H点,∠A=56°,求∠BHC的度数.
三、解答题15.将长度为24的一根铝丝折成各边均为正整数的三角形,这个三角形的三边分别记为a、b、c,且a≤b≤c,请写出满足题意的a、b、c. 16.已知:如图,△ABC的两条高线BD、CE相交于H点,∠A=56°,求∠BHC的度数.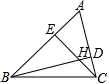 17.探索归纳:
17.探索归纳: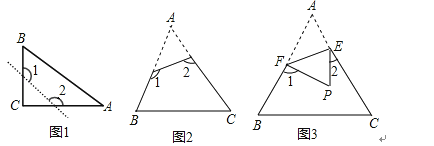 (1)如图1,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )A.90° B.135° C.270° D.315°(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2= (3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是 (4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由. 18.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数.
(1)如图1,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )A.90° B.135° C.270° D.315°(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2= (3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是 (4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由. 18.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数.  19.如图,六边形ABCDEF的内角都相等,CF∥AB.
19.如图,六边形ABCDEF的内角都相等,CF∥AB.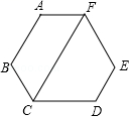 (1)求∠FCD的度数;(2)求证:AF∥CD. 20.如图,已知直线AB,CD,AC上的点M,N,E满足ME⊥NE,∠AME+∠CNE=90°,∠ACD的平分线CG交MN于G,作射线GF∥AB.
(1)求∠FCD的度数;(2)求证:AF∥CD. 20.如图,已知直线AB,CD,AC上的点M,N,E满足ME⊥NE,∠AME+∠CNE=90°,∠ACD的平分线CG交MN于G,作射线GF∥AB.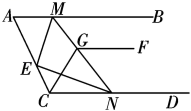 (1)直线AB与CD平行吗?为什么?(2)若∠CAB=66°,求∠CGF的度数.
(1)直线AB与CD平行吗?为什么?(2)若∠CAB=66°,求∠CGF的度数.
参考答案1.C2.C3.A4.C5.A6.C7.C8.A9.115°10.811.60;10012.![]() 13.1214.123°15.解答:∵a+b+c=24,且a+b>c,a≤b≤c, ∴8≤c≤11,即c=8,9,10,11, 故可得(a,b,c)共12组: 当c=11时,有:2,11,11; 3,10,11;4,9,11;5,8,1;6,7,11. 当c=10时,有:4,10,10;5,9,10;6,8,10;7,7,10. 当c=9时,有: 6,9,9;7,8,9. 当c=8时,有:8,8,8.16.∵BD⊥AC,CE⊥AB, ∴∠AEH=∠ADH=90°,在四边形AEHD中,∠AEH=∠ADH=90°,∠A=56°,∴∠EHD=360°-∠AEH-∠ADH-∠A=360°-90°-90°-56°=124°,∵∠BHC与∠EHD是对顶角,∴∠BHC=∠EHD=124°.17.(1)C(2)220°(3)∠1+∠2=180°+∠A (4)∵△EFP是由△EFA折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A,∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.18.解:∵DE=EB ∴设∠BDE=∠ABD=x,∴∠AED=∠BDE+∠ABD=2x,∵AD=DE,∴∠AED=∠A=2x,∴∠BDC=∠A+∠ABD=3x,∵BD=BC,∴∠C=∠BDC=3x,∵AB=AC,∴∠ABC=∠C=3x,在△ABC中,3x+3x+2x=180°,解得x=22.5°,∴∠A=2x=22.5°×2=45°.
13.1214.123°15.解答:∵a+b+c=24,且a+b>c,a≤b≤c, ∴8≤c≤11,即c=8,9,10,11, 故可得(a,b,c)共12组: 当c=11时,有:2,11,11; 3,10,11;4,9,11;5,8,1;6,7,11. 当c=10时,有:4,10,10;5,9,10;6,8,10;7,7,10. 当c=9时,有: 6,9,9;7,8,9. 当c=8时,有:8,8,8.16.∵BD⊥AC,CE⊥AB, ∴∠AEH=∠ADH=90°,在四边形AEHD中,∠AEH=∠ADH=90°,∠A=56°,∴∠EHD=360°-∠AEH-∠ADH-∠A=360°-90°-90°-56°=124°,∵∠BHC与∠EHD是对顶角,∴∠BHC=∠EHD=124°.17.(1)C(2)220°(3)∠1+∠2=180°+∠A (4)∵△EFP是由△EFA折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A,∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.18.解:∵DE=EB ∴设∠BDE=∠ABD=x,∴∠AED=∠BDE+∠ABD=2x,∵AD=DE,∴∠AED=∠A=2x,∴∠BDC=∠A+∠ABD=3x,∵BD=BC,∴∠C=∠BDC=3x,∵AB=AC,∴∠ABC=∠C=3x,在△ABC中,3x+3x+2x=180°,解得x=22.5°,∴∠A=2x=22.5°×2=45°. 19.(1)解:∵六边形ABCDEF的内角相等, ∴∠B=∠A=∠BCD=120°,∵CF∥AB,∴∠B+∠BCF=180°,∴∠BCF=60°,∴∠FCD=60°(2)解:∵∠AFC=360°﹣120°﹣120°﹣60°=60°, ∴∠AFC=∠FCD,∴AF∥CD20.(1)解: 平行,理由如下:
19.(1)解:∵六边形ABCDEF的内角相等, ∴∠B=∠A=∠BCD=120°,∵CF∥AB,∴∠B+∠BCF=180°,∴∠BCF=60°,∴∠FCD=60°(2)解:∵∠AFC=360°﹣120°﹣120°﹣60°=60°, ∴∠AFC=∠FCD,∴AF∥CD20.(1)解: 平行,理由如下:
∵ ME⊥NE, 即∠MEN=90°,
∴∠AEM+∠CEN=90°,
又∵ ∠AME+∠CNE=90°,
∴∠A+∠ECN=180°+180°-(∠AEM+∠CEN+∠AME+∠CNE)
=360°-90°×2
=180°,
∴ AB∥CD.(2)解:∵GF∥AB, AB∥CD,
∴GF∥CD,
∴∠GNC=∠FGN,
∴∠CGF=∠CGN+∠FGN=∠CGN+GNC=180°-∠GCN,
∵AB∥CD,∠CAB=66°,
∴∠ACD=180°-∠CAB=180°-66°=114°
∴CG 平分∠ACD,
∴![]() ,
,
∴∠CGF=180°-∠GCN=180°-57°=123°






