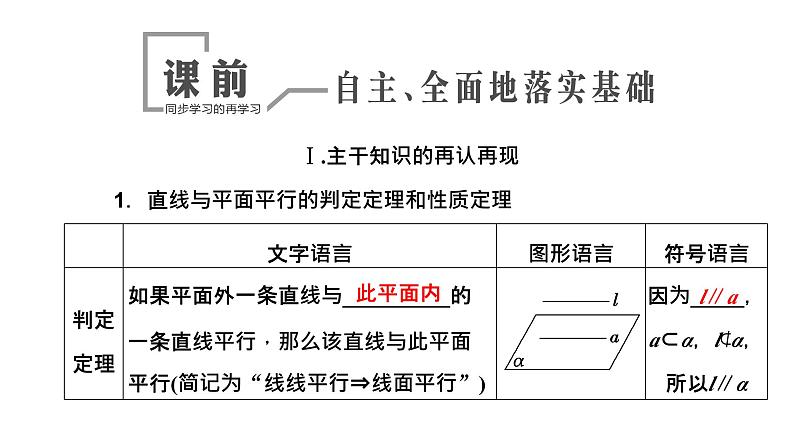
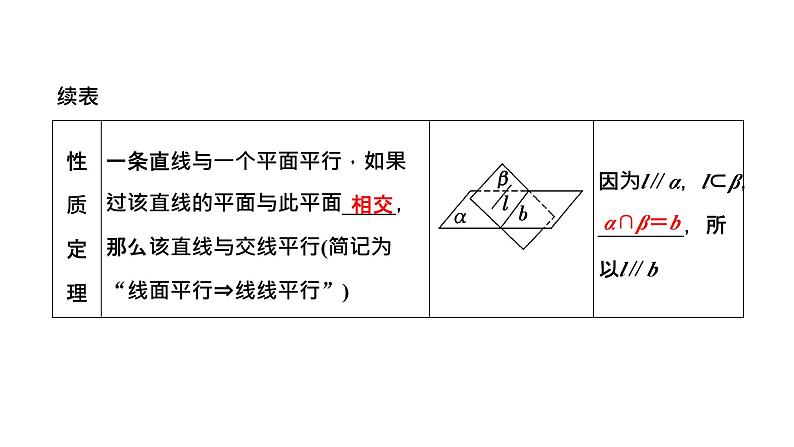
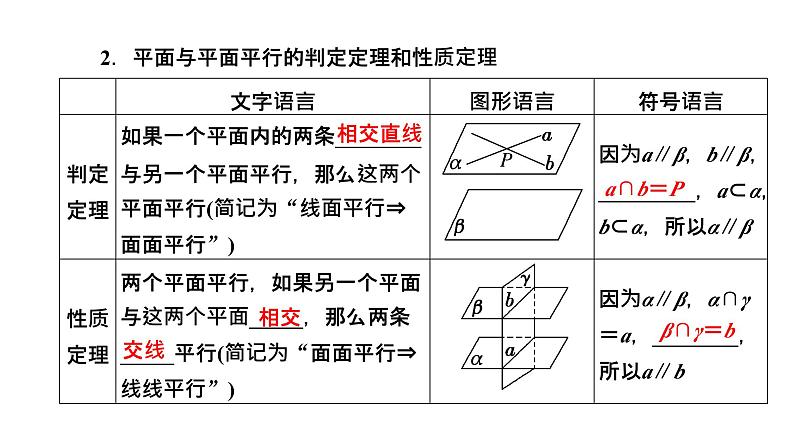
2024年新高考数学一轮复习 第七章 第二节 第二课时 空间直线、平面的平行

课时跟踪检测（四十八） 空间直线、平面的平行

一、全员必做题

1．(2023·哈尔滨模拟)设m，n是两条不同的直线，α，β是不同的平面，则下列说法正确的是( )

A．若m∥α，n∥α，则m∥n

B．若m∥α，m∥β，则α∥β

C．若m∥n，m∥α，n⊄α，则n∥α

D．若m∥α，α∥β，则m∥β

解析：选C对于A，若m∥α，n∥α，则m，n可能平行、相交或异面，故A不正确；对于B，若m∥α，m∥β，则α，β可能相交或平行，故B不正确；对于C，若m∥n，m∥α，n⊄α，则存在l⊂α且m∥l，所以n∥l，由线面平行的判定定理知n∥α，故C正确；对于D，m∥α，α∥β，则m∥β或m⊂β，故D不正确．

2．在三棱锥A-BCD中，点E，F分别在AB，CB上．若AE∶EB＝CF∶FB＝2∶5，则直线AC与平面DEF的位置关系为( )

A．平行  B．相交

C．AC⊂平面DEF  D．不能确定

解析：选A因为AE∶EB＝CF∶FB＝2∶5，所以EF∥AC.又AC⊄平面DEF，EF⊂平面DEF，所以AC∥平面DEF.故选A.

3．已知直线m，n，平面α，β，m⊂α，n⊂α，则“m∥β且n∥β”是“α∥β”的( )

A．充分不必要条件  B．必要不充分条件

C．充要条件  D．既不充分也不必要条件

解析：选B面面平行的判定定理：m⊂α，n⊂α，m∩n＝P，m∥β，n∥β⇒α∥β.所以“m∥β且n∥β”推不出“α∥β”，但“α∥β”可以推得“m∥β且n∥β”，所以“m∥β且n∥β”是“α∥β”的必要不充分条件．

4．(2023·杭州模拟)下列四个正方体图形中，A，B，M，N，P分别为正方体的顶点或其所在棱的中点，能得出AB∥平面MNP的图形是( )

解析：选A对于A，由题意得MN∥AC，NP∥BC，而MP∩NP＝P，AC∩BC＝C，MP⊂平面MNP，NP⊂平面MNP，AC⊂平面ABC，BC⊂平面ABC，故平面MNP∥平面ABC，而AB⊂平面ABC，故AB∥平面MNP，故A正确；对于B，如图1，取MP的中点Q，底面中心O，则NO∥AB，故AB与NQ相交，

故B错误；对于C，MB∥NP，故B∈平面MNP，则AB∩平面MNP＝B，故C错误；对于D，如图2，作平行四边形MNPQ，则AB与MQ相交，故D错误．

5．(多选)在四棱锥P-ABCD中，底面ABCD为梯形，AB∥CD，则( )

A．平面PBC内存在无数条直线与平面PAD平行

B．平面PAD和平面PBC的交线与底面ABCD平行

C．平面PAB和平面PCD的交线与底面ABCD平行

D．平面PAD内任意一条直线都不与BC平行

解析：选ACD设平面PBC∩平面PAD＝l，在平面PBC内存在无数条直线与l平行，且不包含于平面PAD，则在平面PBC内存在无数条直线与平面PAD平行，故A正确；若l∥平面ABCD，l⊂平面PBC，平面PBC∩平面ABCD＝BC，则l∥BC，同理，l∥AD，则BC∥AD，这与四边形ABCD为梯形矛盾，故B错误；设平面PAB∩平面PCD＝m，∵AB∥CD，AB⊄平面PCD，CD⊂平面PCD，∴AB∥平面PCD，又∵AB⊂平面PAB，∴AB∥m，∵AB⊂平面ABCD，m⊄平面ABCD，∴m∥平面ABCD，故C正确；若平面PAD内存在一条直线a与BC平行，则BC∥平面PAD，又∵BC⊂平面ABCD，平面ABCD∩平面PAD＝AD，则BC∥AD，这与四边形ABCD为梯形矛盾，∴平面PAD内任意一条直线都不与BC平行，故D正确．故选A、C、D.

6．(2023·泰安模拟)已知正方体ABCD-A1B1C1D1的棱长为1，点P是面AA1D1D的中心，点Q是面A1B1C1D1的对角线B1D1上一点，且PQ∥平面AA1B1B，则线段PQ的长为( )

A．1           B.          C.  D.

解析：选C连接AB1，AD1，∵点P是平面AA1D1D的中心，∴AD1∩A1D＝P，P是AD1的中点，∵PQ∥平面AA1B1B，PQ⊂平面D1AB1，平面D1AB1∩平面AA1B1B＝AB1，∴PQ∥AB1，即PQ是△D1AB1的中位线，∴PQ＝AB1＝×＝.

7．考查①②两个命题，①⇒l∥α；②⇒l∥α，它们都缺少同一个条件，补上这个条件就可以使其构成真命题(其中l，m为直线，α为平面)，则此条件为________．

解析：①由线面平行的判定定理知l⊄α；②由线面平行的判定定理知l⊄α.

答案：l⊄α

8.如图所示，在正四棱柱ABCD-A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M只需满足条件________，就有MN∥平面B1BDD1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)

解析：连接HN，FH，FN(图略)，则FH∥DD1，HN∥BD，∴平面FHN∥平面B1BDD1，只需M∈FH，则MN⊂平面FHN，∴MN∥平面B1BDD1.

答案：点M在线段FH上(或点M与点H重合，答案不唯一)

9．如图，在正方体ABCD-A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长等于________．

解析：因为EF∥平面AB1C，EF⊂平面ABCD，平面ABCD∩平面AB1C＝AC，所以EF∥AC，所以点F为DC的中点．故EF＝AC＝.

答案：

10.用一个平面去截直三棱柱ABC-A1B1C1，交A1C1，B1C1，BC，AC分别于点E，F，G，H. 若A1A>A1C1，则截面的形状可以为______．(把你认为可能的结果的序号填在横线上)

①一般的平行四边形；②矩形；③菱形；④正方形；⑤梯形．

解析：三棱柱ABC-A1B1C1为直三棱柱，则平面A1B1C1∥平面ABC，截面与平面A1B1C1、平面ABC均相交，则交线EF∥HG，当FG不与B1B平行时，此时EH不平行于FG，四边形EFGH为梯形；当FG∥B1B时，此时EH∥FG，FG⊥EF，当EH≠EF时，四边形EFGH为矩形；当EH＝EF时，四边形EFGH为正方形．

答案：②④⑤

11.已知底面为菱形的四棱锥P-ABCD中，△PAD是边长为2的等边三角形，平面PAD⊥平面ABCD，E，F分别是棱PC，AB上的点，从下面①②③中选取两个作为条件，证明另一个成立．①F是AB的中点；②E是PC的中点；③BE∥平面PFD.

证明：选①F是AB的中点，②E是PC的中点为已知条件，证明③BE∥平面PFD.取PD的中点M，连接ME，MF，所以ME∥CD，ME＝CD，FB∥CD，FB＝CD，ME∥FB，ME＝FB，所以四边形MEBF是平行四边形，BE∥MF，因为BE⊄平面PDF，MF⊂平面PDF，所以BE∥平面PFD.

选②E是PC的中点，③BE∥平面PFD为已知条件，证明①F是AB的中点．取PD的中点M，连接ME，MF，所以ME∥CD，ME＝CD，因为FB∥CD，所以ME∥FB，即平面MEBF∩平面PDF＝FM，因为BE∥平面PFD，BE⊂平面MEBF，所以BE∥MF，所以四边形MEBF是平行四边形，BF＝ME，因为ME＝CD＝AB，所以BF＝AB，即F是AB的中点．

选①F是AB的中点，③BE∥平面PFD为已知条件，证明②E是PC的中点．取CD的中点N，连接BN，EN，所以DN∥FB，DN＝FB，四边形BFDN是平行四边形，BN∥DF，因为BN⊄平面PDF，DF⊂平面PDF，所以BN∥平面PFD，因为BE∥平面PFD，BN∩BE＝B，所以平面PDF∥平面BEN，EN⊂平面BNE，所以EN∥平面PDF，EN⊂平面PDC，平面PDC∩平面PDF＝DP，所以EN∥PD，因为N是CD的中点，所以E是PC的中点．

12．如图所示，已知几何体ABCD-A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，G在BB1上，且AE＝FC1＝B1G＝1，H是B1C1的中点．求证：

(1)E，B，F，D1四点共面；

(2)平面A1GH∥平面BED1F.

证明：(1)如图，在DD1上取一点N使得DN＝1，

连接CN，EN，则AE＝DN＝1，CF＝ND1＝2，

因为CF∥ND1，所以四边形CFD1N是平行四边形，

所以D1F∥CN，

同理四边形DNEA是平行四边形，

所以EN∥AD且EN＝AD，

又BC∥AD且AD＝BC，

所以EN∥BC，EN＝BC，

所以四边形CNEB是平行四边形，

所以CN∥BE，

所以D1F∥BE，

所以E，B，F，D1四点共面.

(2)因为H是B1C1的中点，所以B1H＝，

因为B1G＝1，所以＝，

因为＝且∠FCB＝∠GB1H＝90°，

所以△B1HG∽△CBF，

所以∠B1GH＝∠CFB＝∠FBG，

所以HG∥FB，

因为HG⊄平面BED1F，FB⊂平面BED1F，

所以HG∥平面BED1F，

因为BG＝EA1＝2，BG∥EA1,

所以四边形BEA1G是平行四边形，

所以A1G∥BE，

因为A1G⊄平面BED1F，BE⊂平面BED1F，所以A1G∥平面BED1F，

又HG∩A1G＝G，HG，A1G⊂平面A1GH，

所以平面A1GH∥平面BED1F.

二、重点选做题

1.(2023·重庆联考)如图，四棱柱ABCD-A1B1C1D1中，四边形ABCD为平行四边形，E，F分别在线段DB，DD1上，且＝＝，G在CC1上且平面AEF∥平面BD1G，则＝( )

A.          B.        C.   D.

解析：选B如图所示，延长AE交CD于点H，连接FH，则△DEH∽△BEA，所以＝＝.因为平面AEF∥平面BD1G，平面AEF∩平面CDD1C1＝FH，平面BD1G∩平面CDD1C1＝D1G，所以FH∥D1G.又四边形CDD1C1是平行四边形，所以△DFH∽△C1GD1，所以＝，因为＝＝，所以＝，因为＝，所以FD1＝C1G，DF＝CG，所以＝，故选B.

2.(多选)如图，在棱长均相等的正四棱锥P-ABCD中，O为底面正方形的中心，M，N分别为侧棱PA，PB的中点，下列结论正确的是( )

A．PC∥平面OMN

B．平面PCD∥平面OMN

C．OM⊥PA

D．直线PD与直线MN所成角的大小为90°

解析：选ABC连接AC，如图所示，∵O为底面正方形的中心，∴O为AC中点，又∵M为PA中点，∴OM∥PC，又∵OM⊂平面OMN，PC⊄平面OMN，∴PC∥平面OMN，故A正确；连接BD，同理可证ON∥PD，又∵ON⊂平面OMN，PD⊄平面OMN，∴PD∥平面OMN，又∵PD∩PC＝P，PC∥平面OMN，PC⊂平面PCD，PD⊂平面PCD，∴平面PCD∥平面OMN，故B正确；由于正四棱锥P-ABCD的棱长均相等，且四边形ABCD为正方形，∴AB2＋BC2＝PA2＋PC2＝AC2，∴PA⊥PC，又∵OM∥PC，∴OM⊥PA，故C正确；∵M，N分别为侧棱PA，PB的中点，∴MN∥AB，∵四边形ABCD为正方形，∴CD∥AB，∴直线PD与直线CD所成的角即为直线PD与直线MN所成的角，∴∠PDC即为直线PD与直线MN所成的角，又∵△PDC为正三角形，∴∠PDC＝60°，∴直线PD与直线MN所成的角为60°，故D不正确．故选A、B、C.

3．如图①，在棱长为2的正方体ABCD-A1B1C1D1木块中，E是CC1的中点．

(1)求四棱锥E-ABC1D1的体积；

(2)要经过点A将该木块锯开，使截面平行于平面BD1E，在该木块的表面应该怎样画线？(请在图②中作图，并写出画法，不必说明理由．)

解：(1)在正方体ABCD-A1B1C1D1中，连接AD1，BC1，EA，EB，ED1，AC1，如图，AB∥C1D1且AB＝C1D1，则四边形ABC1D1为平行四边形，有S▱ABC1D1＝2S△ABC1，三棱锥E-ABC1的体积VE-ABC1＝VA-BC1E＝S△BC1E·AB＝··AB＝×2×1×2＝，所以四棱锥E-ABC1D1的体积VE-ABC1D1＝2VE-ABC1＝.

(2)取棱DD1的中点F，连接AF，CF，AC，则FC，FA，CA就是所求作的线，如图，在正方体ABCD-A1B1C1D1中，连接EF，因为E是CC1的中点，F是DD1的中点，

则EF∥CD∥BA，且EF＝CD＝BA，于是得四边形ABEF是平行四边形，有AF∥BE，而BE⊂平面BD1E，AF⊄平面BD1E，因此AF∥平面BD1E，又FD1∥CE，FD1＝CE，即四边形CED1F为平行四边形，则CF∥ED1，又ED1⊂平面BD1E，CF⊄平面BD1E，于是有CF∥平面BD1E，而CF∩AF＝F，CF，AF⊂平面AFC，从而平面AFC∥平面BD1E，所以FC，FA，CA就是所求作的线．