中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习08（含答案）

中考数学三轮冲刺《锐角三角函数实际问题》

解答题冲刺练习08

1.如图,已知长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°，黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后，直接打通长江路（即修建AB路段）．

问：打通长江路后从A地道B地可少走多少路程？（参考数据：≈1.4，≈1.7）

2.如图，四边形ABCD是一片水田，某村民小组需计算其面积，测得如下数据：

∠A＝90°，∠ABD＝60°，∠CBD＝54°，AB＝200 m，BC＝300 m.

请你计算出这片水田的面积(参考数据：sin54°≈0.809，cos54°≈0.588，tan54°≈1.376，≈1.732).

3.如图，一楼房AB后有一假山，其坡度为i=1∶，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC=25米，与亭子距离CE=20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高.(注：坡度i是指坡面的铅直高度与水平宽度的比)

4.如图1，某同学家的一面窗户上安装有遮阳篷，图2和图3是截面示意图，CD是遮阳篷，窗户AB为1.5米，BC为0.5米．该遮阳篷有伸缩功能．如图2，该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°，遮阳篷CD正好将进入窗户AB的阳光挡住；如图3，该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°，将遮阳篷收缩成CD′时，遮阳篷正好完全不挡进入窗户AB的阳光．

（1）计算图3中CD′的长度比图2中CD的长度收缩了多少米；（结果保留根号）

（2）如果图3中遮阳篷的长度为图2中CD的长度，请计算该遮阳落在窗户AB上的阴影长度为多少米？（请在图3中画图并标出相应字母，然后再计算）

5.如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B、C两地相距120海里．

（1）求出此时点A到岛礁C的距离；

（2）若“中海监50”从A处沿AC方向向岛礁C驶去，当到达点A′时，测得点B在A′的南偏东75°的方向上，求此时“中国海监50”的航行距离．（注：结果保留根号）

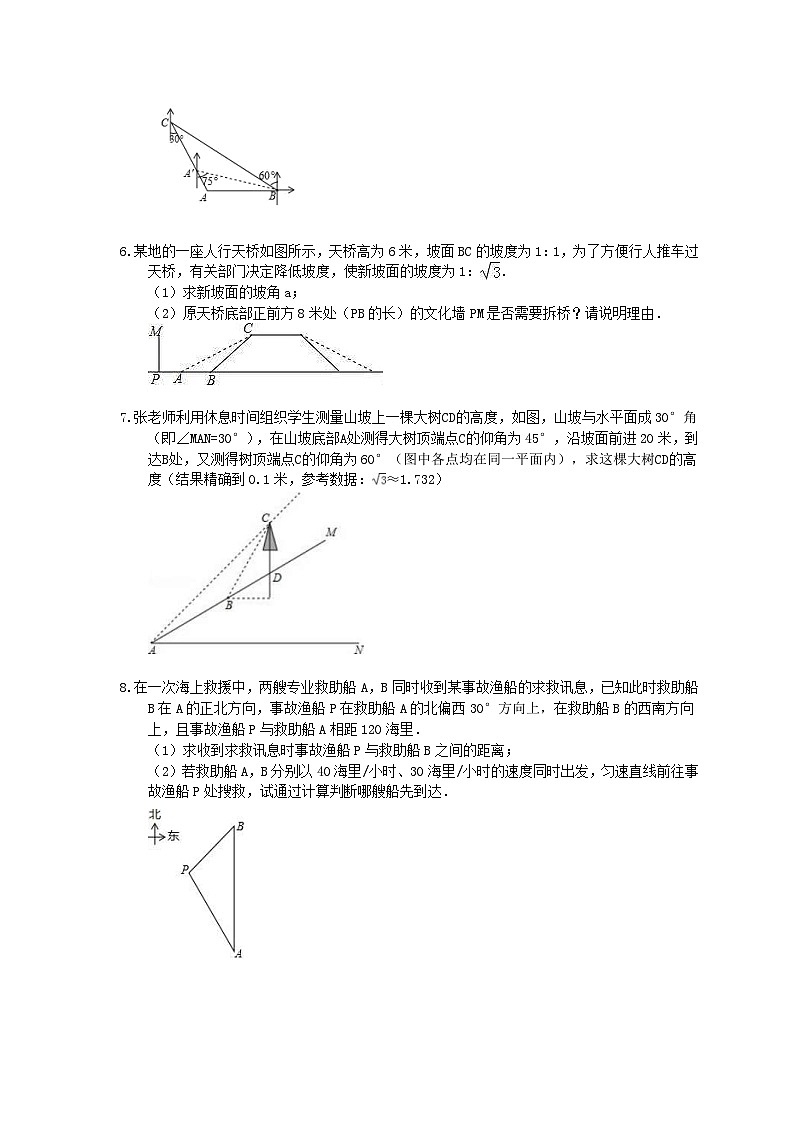
6.某地的一座人行天桥如图所示，天桥高为6米，坡面BC的坡度为1：1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1：．

（1）求新坡面的坡角a；

（2）原天桥底部正前方8米处（PB的长）的文化墙PM是否需要拆桥？请说明理由．

7.张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据：≈1.732）

8.在一次海上救援中，两艘专业救助船A，B同时收到某事故渔船的求救讯息，已知此时救助船B在A的正北方向，事故渔船P在救助船A的北偏西30°方向上，在救助船B的西南方向上，且事故渔船P与救助船A相距120海里．
（1）求收到求救讯息时事故渔船P与救助船B之间的距离；
（2）若救助船A，B分别以40海里/小时、30海里/小时的速度同时出发，匀速直线前往事故渔船P处搜救，试通过计算判断哪艘船先到达．

9.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=,sinB=,AD=1．

（1）求BC的长；（2）求tan∠DAE的值．

10.A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627，tanβ=1.373．为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区，请说明理由．

0.中考数学三轮冲刺《锐角三角函数实际问题》解答题冲刺练习08（含答案）参考答案

一         、解答题

1.解：如图所示：过点C作CD⊥AB于点D，

在Rt△ACD中，∠CAD=30°，AC=20km，则CD=10km，AD=10km，

在Rt△BCD中，∠CBD=45°，CD=10km，故BD=10km，BC=10km，

则AC+BC﹣AB=20+10﹣10﹣10≈7（km），

答：打通长江路后从A地道B地可少走7km的路程．

2.解：如图，过点C作CM⊥BD于点M.

∵∠A＝90°，∠ABD＝60°，

∴∠ADB＝30°，

∴BD＝2AB＝400 (m)，

∴AD＝AB＝200(m)，

∴S△ABD＝×200×200＝20 000(m2)，

∵∠CMB＝90°，∠CBD＝54°，

∴CM＝BC·sin54°＝242.7(m)，

∴S△BCD＝×400×242.7＝48 540(m2)，

∴这片水田的面积为20 000＋48 540＝83 180(m2).

3.解：过点E作EF⊥BC的延长线于F，EH⊥AB于点H，

在Rt△CEF中，

∵i===tan∠ECF，

∴∠ECF=30°.

∴EF=CE=10米，CF=10米.

∴BH=EF=10米，

HE=BF=BC＋CF=(25＋10)米.

在Rt△AHE中，∵∠HAE=45°，

∴AH=HE=(25＋10)米.

∴AB=AH＋HB=(35＋10)米.

答：楼房AB的高为(35＋10)米.

4.

5.解：

6.解：（1）∵新坡面的坡度为1：，∴tanα=tan∠CAB==，

∴∠α=30°．答：新坡面的坡角a为30°；

（2）文化墙PM不需要拆除．过点C作CD⊥AB于点D，则CD=6，

∵坡面BC的坡度为1：1，新坡面的坡度为1：，∴BD=CD=6，AD=6，

∴AB=AD﹣BD=6﹣6＜8，∴文化墙PM不需要拆除．

7.

8.解：

9.解：（1）在△ABC中，∵AD是BC边上的高，∴∠ADB=∠ADC=90°．

 ∵cosC=，∴∠C=45°． 在△ADC中，∵∠ADC=90°，AD=1，∠C=45°，∴DC=AD=1．

在△ADB中，∵∠ADB=90°，sinB==，AD=1，∴AB==3．

∴BD==2 ．∴BC=BD+DC=2+1． 

（2）∵AE是BC边上的中线，∴CE=BC=+ ．∴DE=CE﹣CD=﹣．∴tan∠DAE==﹣．

10.解：AB不穿过风景区．理由如下：如图，过C作CD⊥AB于点D，

根据题意得：∠ACD=α，∠BCD=β，

则在Rt△ACD中，AD=CD•tanα，在Rt△BCD中，BD=CD•tanβ，

∵AD+DB=AB，∴CD•tanα+CD•tanβ=AB，∴CD==（千米）．

∵CD=50＞45，∴高速公路AB不穿过风景区．