初中数学沪科版八年级下册18.1 勾股定理课后复习题

第18章　勾股定理

18.1　勾股定理

基础过关全练

知识点1　勾股定理

1.(2022安徽庐江期中)Rt△ABC的斜边的长为13,其中一条直角边的长为12,则另一条直角边的长为              (　　)

A.5　　　　B.6　　　　C.7　　　　D.9

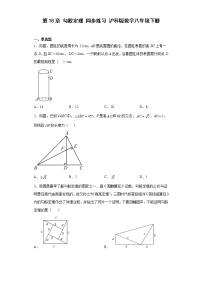
2.【新独家原创】【数形结合思想】由两个直角三角形和三个正方形组成的图形如图所示,部分边的长度如图,则阴影部分的面积是              (　　)

A.16　　　　B.25　　　　C.36　　　　D.48

3.【教材变式·P55练习T1变式】在△ABC中,∠C=90°.

(1)若AC=4,BC=7,求AB的长;

(2)若∠A=30°,AC=2,求BC的长.

知识点2　勾股定理的证明

4.【割补法】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形按如图所示的方式摆放时,可以用“面积法”来证明.已知两个全等的直角三角形的直角边长分别为a,b,斜边长为c,∠DAB=90°,求证:a2+b2=c2.

知识点3　勾股定理的应用

5.【学科素养·应用意识】

如图,小明和小华同时从P处分别向北偏东60°和南偏东30°方向出发,他们的速度分别是3 m/s和4 m/s,则20 s后他们之间的距离为              (　　)

A.70 m　　　　B.80 m         C.90 m　　　　D.100 m

6.【主题教育·中华优秀传统文化】(2022安徽合肥四十八中期中)《九章算术》中有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十而斜东北与乙会.问甲、乙行各几何?”大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10,后又向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多少?设甲、乙二人从出发到相遇的时间为x,根据题意,下列方程正确的是              (　　)

A.(3x)2+(7x)2=102                        B.(3x)2+102=(7x)2

C.(3x)2+102=(7x-10)2                    D.(3x+10)2+102=(7x)2

能力提升全练

7.【数形结合思想】(2022天津中考,10,)如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴.若AB=6,OA=OB=5,则点A的坐标是              (　　)

A.(5,4)          B.(3,4)          C.(5,3)         D.(4,3)

8.【新考法】(2022浙江金华中考,7,)城市某区域的示意图如图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是              (　　)

A.超市　　　　B.医院　　　　C.体育场　　　　D.学校

9.(2022安徽安庆石化一中期中,3,)如果直角三角形的两边长分别是3,4,那么斜边长是(　　)

A.5　　　　   B.　　　　D.5或4

10.【主题教育·中华优秀传统文化】(2022江苏泰州中考,14,)如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为　　　　. 

11.(2021湖南岳阳中考,15,)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线长恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为　　　　　　　. 

12.(2021安徽合肥庐阳期末,12,)如图所示,在建筑工地上,为了支撑一堵墙,用一根长为5 m的木材顶端撑在墙上,底端撑在地面上,BO=4 m,现为了增加支撑效果,底端向前移动1.5 m,问:顶端需上移多少米?在这个问题中,设顶端上移x米,则可列方程为　　　　　　　　　. 

13.【学科素养·模型观念】(2022四川眉山中考,22,)数学实践活动小组去测量眉山市某标志性建筑物的高CD.如图,在楼前平地A处测得楼顶C处的仰角为30°,沿AD方向前进60 m到达B处,测得楼顶C处的仰角为45°,求此建筑物的高.(结果保留整数.参考数据:≈1.73)

14.(2021安徽合肥四十五中期末,17,)《中华人民共和国道路交通安全法实施条例》规定:小汽车在城街路上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪间的距离为50 m,这辆小汽车超速了吗?(参考数据:1 m/s=3.6 km/h)

15.【学科素养·应用意识】(2022广西防城港防城期中,25,)学过“勾股定理”后,八(1)班数学兴趣小组来到操场上测量旗杆AB的高度.小华测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米(如图1),小明拉着绳子的下端往后退,当他将绳子拉直时,小凡测得此时小明拉绳子的手到地面的距离CD为1米,到旗杆的距离CE为8米(如图2).(1)设AB的长为x米,则绳子的长为　　　米,AE的长为　　　　米(用含x的代数式表示); 

(2)请你求出旗杆的高度AB.

图1                图2

素养探究全练

16.【模型观念】(2022安徽潜山期中)如图,△ABC中,∠ACB=90°,AB=10 cm,BC=6 cm,若点P从点A出发,以每秒2 cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB,求出此时t的值;

(2)若点P恰好在∠BAC的平分线上,求t的值.

                           备用图1            备用图2

答案全解全析

基础过关全练

1.A　根据题意,由勾股定理得另一条直角边的长==5.

2.B　根据勾股定理得AB==5,

∴EF=AB=5,

在Rt△EPF中,EP2+PF2=EF2=25,正方形QMPE的面积为EP2,正方形PSTF的面积为PF2,

∴阴影部分的面积是25.

3.解析　(1)∵∠C=90°,AC=4,BC=7,

∴AB=.

(2)∵∠C=90°,∠A=30°,

∴AB=2BC.

∵BC2+AC2=AB2,AC=2,

∴BC2+(2)2=(2BC)2,

∴BC=2或BC=-2(舍去),

∴BC=2.

4.证明　如图,连接DB,过点D作BC边上的高DF,垂足为F,则DF=EC=b-a.

∵S四边形ADCB=S△ACD+S△ABC=ab,

且S四边形ADCB=S△ADB+S△DCB=a(b-a),

∴a(b-a),

∴a2+b2=c2.

5.D　根据题意得∠APB=180°-60°-30°=90°,PA=3×20=60(m),PB=4×20

=80(m),根据勾股定理得AB==100(m).

6.C　出发x(时间)后二人在B处相遇,

这时乙共行AB=3x,甲共行AC+BC=7x,

∵AC=10,

∴BC=7x-10.

又∵∠A=90°,

∴AB2+AC2=BC2,

∴(3x)2+102=(7x-10)2.

能力提升全练

7.D　设AB与x轴交于点C,

∵OA=OB,OC⊥AB,AB=6,

∴AC=AB=3,

由勾股定理得OC==4,

∴点A的坐标为(4,3).

8.A　根据题意可以画出相应的平面直角坐标系,然后根据勾股定理,可以得到原点O到超市、学校、体育场、医院的距离,再比较大小.

根据学校和体育场的位置与坐标可以确定坐标系的原点O的位置如图所示,则点O到超市的距离为,点O到学校的距离为,点O到体育场的距离为,点O到医院的距离为,∴离原点最近的是超市.

9.D　当4是直角边长时,斜边长==5;

当4是斜边长时,斜边长为4.故斜边长为5或4.

10.

解析　按照“马走日”的规则,走两步后的落点与出发点间的最短距离为.

11.(x-6.8)2+x2=102

解析　门高AB为x尺,则门的宽为(x-6.8)尺,AC=1丈=10尺,

依题意得BC2+AB2=AC2,即(x-6.8)2+x2=102.

12.(x+3)2+(4-1.5)2=52

解析　在△AOB中,∠AOB=90°,BO=4 m,AB=5 m,

∴AO==3(m).顶端上移x m,依题意得(x+3)2+(4-1.5)2=52.

13.解析　在Rt△BCD中,∠CBD=45°,设CD为x m,则BD=CD=x m,

∴AD=BD+AB=(60+x)m.

在Rt△ACD中,∠CAD=30°,

∴AC=2CD=2x.

∵AC2=CD2+AD2,

∴(2x)2=x2+(60+x)2,

∴x2-60x-1 800=0,

∴x1=30+30≈82,x2=30-30(不合题意,舍去).

答:此建筑物的高度约为82 m.

14.解析　在Rt△ABC中,AC=30 m,AB=50 m.

根据勾股定理可得BC==40(m),

∴小汽车的速度v==20(m/s)=72(km/h).

∵72 km/h>70 km/h,

∴这辆小汽车超速了.

答:这辆小汽车超速了.

15.解析　(1)AB的长为x米,则绳子的长为(x+1)米,AE的长为(x-1)米.

(2)在Rt△ACE中,AC=(x+1)米,AE=(x-1)米,CE=8米,由勾股定理得(x-1)2+82=(x+1)2,

解得x=16.

答:旗杆的高度AB为16米.

素养探究全练

16.解析　(1)在Rt△ABC中,AC==8(cm),

因为P在AC上,且满足PA=PB,

所以PA=PB=2t(cm),PC=(8-2t)cm,

在Rt△PCB中,PC2+CB2=PB2,

即(8-2t)2+62=(2t)2,解得t=,

所以当t=时,PA=PB.

(2)因为点P在∠BAC的平分线上,所以分两种情况:

①如图,过点P作PE⊥AB于点E,CP=(2t-8)cm,AC=AE=8 cm,

此时BP=(14-2t)cm,PE=PC=(2t-8)cm,BE=10-8=2(cm).

在Rt△BEP中,PE2+BE2=BP2,

即(2t-8)2+22=(14-2t)2,解得t=,

当t=时,P在∠BAC的平分线上.

②当点P与点A重合时,P点经过的长度为8+6+10=24(cm),

所以t==12.

综上所述:t=或12.