沪科版八年级上册15.4 角的平分线教学课件ppt

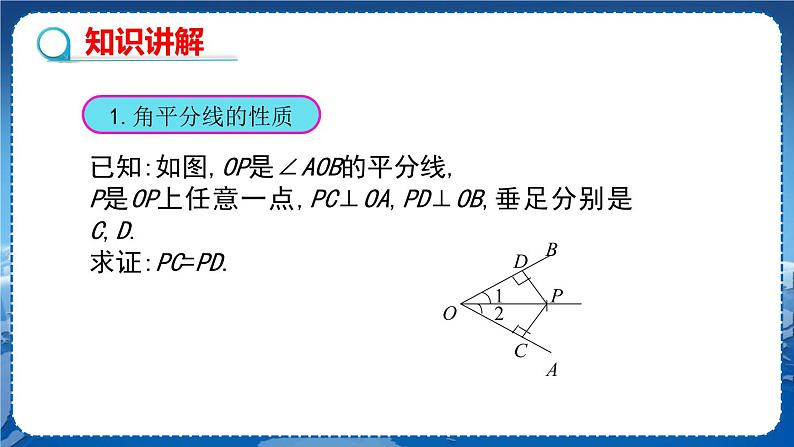
教学目标

1.会证明角平分线的性质定理及逆定理；

2.会运用角平分线的性质定理及逆定理解决有关的数学问题.

教学重难点

重点： 角平分线的性质定理及其逆定理.

难点：利用角平分线的性质定理及其逆定理解决实际问题.

教学过程

知识回顾

1.你能利用尺规作出角平分线吗?

2.你还记得角平分线上的点有什么性质吗? 怎么证明这一结论？

探究新知

探究1：角平分线的性质

【教师提问】请同学们拿出准备好的折纸与剪刀，自己动手，剪一个角，把剪好的角对折，使角的两边叠合在一起，再把纸片展开，你看到了什么？把对折的纸片再任意折一次，然后把纸片展开，又看到了什么？

【学生活动】先独立思考，再与同伴交流

第一次对折后的折痕是这个角的平分线；再折一次，又会出现两条折痕，而且这两条折痕是等长的.这种方法可以做无数次，所以这种等长的折痕可以折出无数对.

【教师】折出如图所示的折痕PD、PE.

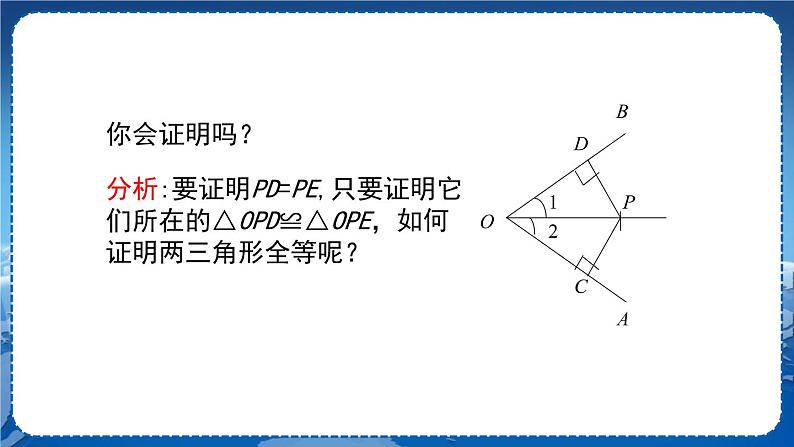
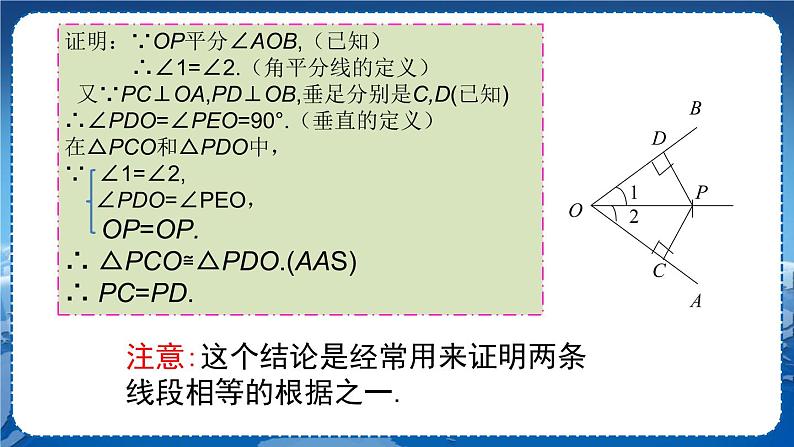
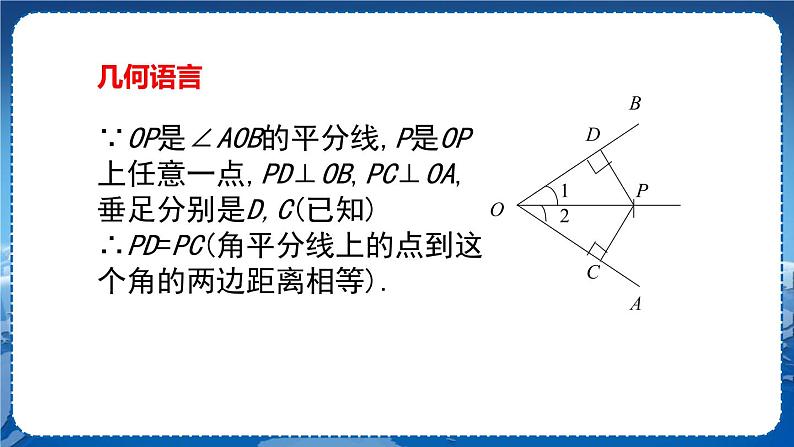
【教师提问】按照折纸的顺序画出一个角的三条折痕，并度量所画PD、PE是否等长？

【学生活动】先独立思考，再与同伴交流.

PD＝PE

【教师】我们猜想角的平分线上的点到角的两边的距离相等.

【教师提问】你能证明这一性质吗？

【学生活动】先独立思考，再与同伴交流.

已知：如图,OP是∠AOB的平分线,P是OP上任意一点,PC⊥OA,PD⊥OB,垂足分别是C,D.

求证：PC＝PD.

分析：要证明PC＝PD,只要证明它们所在的△OPC≌△OPD，如何证明两三角形全等呢？

证明：∵ OP平分∠AOB,（已知）

∴ ∠1＝∠2.（角平分线的定义）

又∵ PC⊥OA,PD⊥OB,垂足分别是C,D(已知)

∴ ∠PCO＝∠PDO＝90°.（垂直的定义）

在△PCO和△PDO中，

∵

∴  △PCO≌△PDO.(AAS)

∴  PC＝PD.

于是我们得角的平分线的性质：

在角的平分线上的点到角的两边的距离相等.

注意：这个结论是经常用来证明两条线段相等的根据之一.

【教师提问】能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话.

【互动总结】(学生总结，老师点评)

几何语言

∵ OP是∠AOB的平分线,P是OP上任意一点,PD⊥OB,PC⊥OA,

垂足分别是D,C(已知)

∴ PD＝PC(角平分线上的点到这个角的两边距离相等).

典型例题

例1  已知：如图,在△ABC 中,AD是它的角平分线,且BD＝CD,DE⊥AB,

DF⊥AC,垂足分别是E,F.求证：EB＝FC.

【分析】根据角平分线的性质得到DE＝DF，再根据HL证△BED≌△CFD,从而得到EB＝FC.

证明：∵ AD是∠BAC的平分线， DE⊥AB, DF⊥AC，

∴  DE＝DF , ∠DEB＝∠DFC＝90 °.

在Rt△BDE 和 Rt△CDF中，

∴  Rt△BDE ≌ Rt△CDF(HL).

∴  EB＝FC.

【互动总结】(学生总结，老师点评)

本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键.

探究2：角平分线的判定

你能写出定理 ：“角平分线上的点到这个角的两边距离相等”的逆命题吗?

逆命题：在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.

它是真命题吗?

如果是，请你证明它.

已知：如图所示,PD＝PC, PD⊥OB,PC⊥OA, 垂足分别是D,C.

求证：点P在∠AOB的平分线上.

证明：∵ PD⊥OB,PC⊥OA,

∴ △POD和△POC都是直角三角形.

∵ PD＝PC,OP＝OP,

∴ Rt△POD≌Rt△POC(HL),

∴ ∠POD＝∠POC ,

∴ OP是∠AOB的平分线，即点P在∠AOB的平分线上.

定理   角的内部到角两边距离相等的点在角的平分线上.

老师提示：这个结论又经常用来证明点在直线上(或直线经过某一点).

典型例题

例2　如图，在△ABC中，∠BAC＝60°，点D在BC上，AD＝10，DE⊥AB，DF⊥AC，垂足分别为E，F，且DE＝DF，求DE的长.

解：∵  DE＝DF， DE⊥AB，DF⊥AC，

∴ AD平分∠BAC.

∵  ∠BAC＝60°，

∴ ∠BAD＝∠CAD＝30°.

在Rt△ADE中， ∠EAD＝30°,AD＝10,

∴ DE＝ AD＝5.

例3　如图，在Rt △ABC中，AC＝BC,∠C＝90°，AP平分∠BAC交BC于点P，若PC＝4，AB＝14.

（1）求△APB的面积；

（2）求△PDB的周长.

解：（1）如图，过点P 作PD ⊥AB,

由角平分线的性质，可知，PD＝PC＝4，

·AB·PD＝28.

（2）在Rt△APC和Rt△APD中，

     PC＝PD，AP＝AP，

∴ Rt△ APC ≌Rt△ APD(HL)，

∴ AC＝ AD ＝ BC.

＝PD+PB+DB＝PC+PB+DB＝AD+DB＝AB＝14.

课堂练习

1.角平分线上的点到______________距离相等；到一个角的两边距离相等的点都在_____________.

2.如图，∠AOB＝60°，PD⊥OA于D，PE⊥OB于E，且PD＝PE，则

∠1＝_________.

3.如图,求作一点P,使PC＝PD,并且点P到∠AOB的两边的距离相等.

4.如图，已知AD∥BC，P是∠BAD与 ∠ABC的平分线的交点，PE⊥AB于E，且PE＝3，求AD与BC之间的距离.

参考答案

1. 这个角的两边   这个角的平分线上

 2. 30°

3.解：如图所示：

4.解：过点P作MN⊥AD于点M，交BC于点N.

∵  AD∥BC，∴  MN⊥BC，

MN的长即为AD与BC之间的距离.

∵  AP平分∠BAD, PM⊥AD , PE⊥AB，

∴  PM＝ PE.

同理，PN＝ PE.

∴  PM＝ PN＝ PE＝3.

∴  MN＝6.即AD与BC之间的距离为6.

课堂小结

1.角平分线的性质定理

2.符号表示

∵ OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E，∴ PD＝PE.

3.角平分线的判定定理

4.符号表示

∵ PD＝PE,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),

∴ 点P在∠AOB的平分线上.

布置作业

教材习题15.4（2）第1,2题

板书设计

第2课时角平分线的判定与性质

1.角平分线的性质定理

2.角平分线的判定定理

教学反思

教学反思

教学反思

教学反思

教学反思