资料中包含下列文件,点击文件名可预览资料内容



还剩13页未读,
继续阅读
所属成套资源:2022-2023学年九年级下册数学单元卷(人教版)
成套系列资料,整套一键下载
第二十六章 反比例函数(基础卷)——2022-2023学年九年级下册数学单元卷(人教版)
展开
这是一份第二十六章 反比例函数(基础卷)——2022-2023学年九年级下册数学单元卷(人教版),文件包含第二十七章反比例函数基础卷解析版docx、第二十七章反比例函数基础卷原卷版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。
班级 姓名 学号 分数
第二十六章 反比例函数(A卷·知识通关练)
核心知识1反比例函数图像与性质
1.(2022秋•定远县校级月考)下列函数:①y=x﹣2②y=﹣③y=﹣1④y=,y是x的反比例函数的个数有( )
A.0个 B.1个 C.2个 D.3个
【分析】利用反比例函数定义进行解答即可.
【解答】解:①是一次函数,不是反比例函数;
②是反比例函数;
③不是反比例函数;
④不是反比例函数;
共1个,
故选:B.
【点评】此题主要考查了反比例函数的定义,判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y=(k为常数,k≠0)或y=kx﹣1(k为常数,k≠0).
2.(2022秋•东平县校级月考)函数y=和y=kx﹣k(k≠0)在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
【分析】分别根据反比例函数及一次函数图象的特点对四个选项进行逐一分析即可.
【解答】解:由反比例函数y=的图象在一、三象限可知,﹣k>0,∴k<0,∴一次函数y=kx﹣k的图象经过一、二、四象限,故A、C选项错误,B选项正确;
由反比例函数y=的图象在二、四象限可知,﹣k<0,∴k>0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故D选项错误;
故选:B.
【点评】本题考查的是反比例函数及一次函数图象,解答此题的关键是先根据反比例函数所在的象限判断出k的符号,再根据一次函数的性质进行解答.
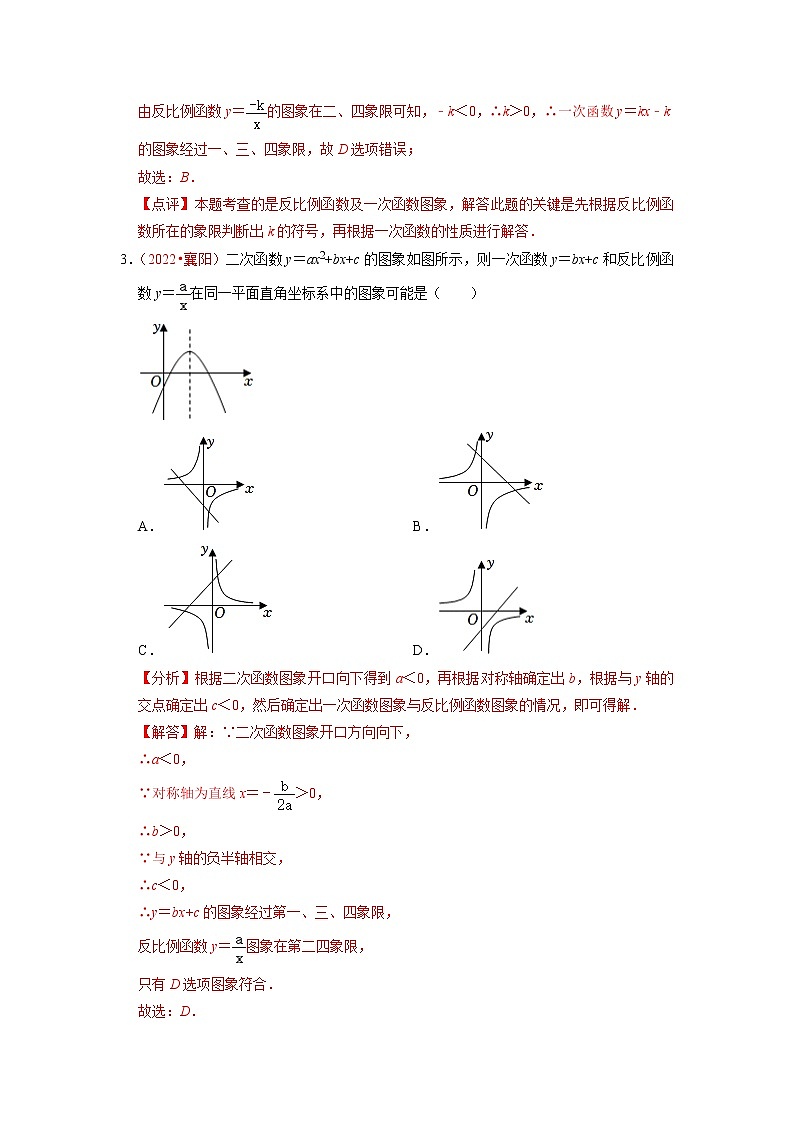
3.(2022•襄阳)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【分析】根据二次函数图象开口向下得到a<0,再根据对称轴确定出b,根据与y轴的交点确定出c<0,然后确定出一次函数图象与反比例函数图象的情况,即可得解.
【解答】解:∵二次函数图象开口方向向下,
∴a<0,
∵对称轴为直线x=﹣>0,
∴b>0,
∵与y轴的负半轴相交,
∴c<0,
∴y=bx+c的图象经过第一、三、四象限,
反比例函数y=图象在第二四象限,
只有D选项图象符合.
故选:D.
【点评】本题考查了二次函数的图形,一次函数的图象,反比例函数的图象,熟练掌握二次函数的有关性质:开口方向、对称轴、与y轴的交点坐标等确定出a、b、c的情况是解题的关键.
4.(2022•菏泽)根据如图所示的二次函数y=ax2+bx+c的图象,判断反比例函数y=与一次函数y=bx+c的图象大致是( )
A. B. C. D.
【分析】先根据二次函数的图象,确定a、b、c的符号,再根据a、b、c的符号判断反比例函数y=与一次函数y=bx+c的图象经过的象限即可.
【解答】解:由二次函数图象可知a>0,c<0,
由对称轴x=﹣>0,可知b<0,
所以反比例函数y=的图象在一、三象限,一次函数y=bx+c图象经过二、三、四象限.
故选:A.
【点评】本题主要考查二次函数图象的性质、一次函数的图象的性质、反比例函数图象的性质,关键在于通过二次函数图象推出a、b、c的取值范围.
5.(2022•安顺)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b和反比例函数y=(c≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
【分析】直接利用二次函数图象经过的象限得出a,b,c的取值范围,进而利用一次函数与反比例函数的性质得出答案.
【解答】解:∵二次函数y=ax2+bx+c的图象开口向上,
∴a>0,
∵该抛物线对称轴位于y轴的右侧,
∴a、b异号,即b<0.
∵抛物线交y轴的负半轴,
∴c<0,
∴一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=(c≠0)在二、四象限.
故选:A.
【点评】此题主要考查了反比例函数、一次函数、二次函数的图象,正确把握相关性质是解题关键.
6.(2022春•钱塘区期末)描点法是画未知函数图象的常用方法.请判断函数的图象可能为( )
A. B.
C. D.
【分析】根据反比例函数的性质可知函数y=在第一、三象限,对称中心为原点,根据函数平移的规律,把y=向左平移1个单位得到y=,对称中心为(﹣1,0),据此即可判断.
【解答】解:∵k=1,
∴函数y=在第一、三象限,对称中心为原点,
把y=向左平移1个单位得到y=,对称中心为(﹣1,0),
故选:D.
【点评】本题考查了反比例函数的图象和性质,函数y=与函数y=的关系是解题的关键.
7.(2022•崂山区二模)已知一次函数y=abx+bc的图象如图所示,则二次函数y=ax2+bx+c和反比例函数y=在同一坐标系内的图象可能是( )
A. B.
C. D.
【分析】根据一次函数的图象所经过的象限可以判定a、b、c的符号,从而得到ab<0,bc>0,然后根据二次函数和反比例函数经过的象限,判定a、b、c的符号,从而得出ab和bc的符号,看是否一致.
【解答】解:∵一次函数y=abx+bc的图象经过第一、二、四象限,
∴ab<0,bc>0.
∴反比例函数y=经过第二、四象限,故A、C不合题意,B、D符合题意;
B、二次函数y=ax2+bx+c图象开口向上,对称轴为y轴,交y的负半轴,
∴a>0,b=0,c<0,
∴ab=0,bc=0,故B不合题意;
D、二次函数y=ax2+bx+c图象开口向下,对称轴在y轴右,交y的正半轴,
∴a<0,b>0,c>0,
∴ab<0,bc>0,故D符合题意;
故选:D.
【点评】本题考查了二次函数图象,一次函数图象,反比例函数图象,根据二次函数图象判断出a、b、c的符号情况是解题的关键.
8.(2022•平泉市一模)如图,把函数y=(x>0)和函数y=﹣(x>0)的图象画在同一平面直角坐标系中,则坐标系的横轴可能是( )
A.l1 B.l2 C.l3 D.l4
【分析】根据反比例函数k的取值分析即可.
【解答】解:在函数y=(x>0)和函数y=﹣(x>0)中,
∵2>0,﹣4<0,
∴函数y=(x>0)的图象在第一象限,函数y=﹣(x>0)的图象在第四象限,
∵|﹣4|>|2|,
∴y=(x>0)的图象更靠近坐标轴,
∴坐标系的横轴可以是l2,
故选:B.
【点评】本题考查了反比例函数的图象,熟练掌握反比例函数的性质是解题的关键.
9.(2021秋•房县期末)如图,点P(﹣2a,a)是反比例函数y=的图象与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
【分析】根据圆的对称性以及反比例函数的对称性可得,阴影部分的面积等于圆的面积,即可求得圆的半径,再根据P在反比例函数的图象上,以及在圆上,即可求得k的值.
【解答】解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π.
解得:r=2.
∵点P(﹣2a,a)是反比例函数y=(k<0)与⊙O的一个交点.
∴﹣2a2=k且=r.
∴a2=8.
∴k=﹣2×8=﹣16,
则反比例函数的解析式是:y=﹣.
故选:D.
【点评】本题主要考查反比例函数图象的对称性的知识点,解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系.
10.(2021秋•龙泉驿区期中)如图,过原点的一条直线与反比例函数(k≠0)的图象分别交于A、B两点,若A点的坐标为(3,﹣5),则B点的坐标为( )
A.(3,﹣5) B.(﹣5,3) C.(﹣3,+5) D.(+3,﹣5)
【分析】根据关于原点对称的两点横坐标,纵坐标都互为相反数即可解答.
【解答】解:∵反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称,
∴它的另一个交点的坐标是(﹣3,+5).
故选:C.
【点评】此题考查了反比例函数图象的对称性.反比例函数的图象关于原点对称.
11.(2022秋•石阡县月考)对于反比例函数的叙述错误的是( )
A.其图象关于原点对称
B.点在其图像上
C.当x<0时,y的值随x的值的增大而增大
D.若(x1,y1),(x2,y2)为其函数图象上的两点,且x1x2>0,则y1y2<0
【分析】根据反比例函数的图象和性质,以及反比例函数图象上点的坐标特征依次进行判断即可.
【解答】解:∵反比例函数的图象是中心对称图形,
∴其图象关于原点对称,
故A选项不符合题意;
当x=时,y=﹣1,
∴点A(,﹣1)在其图象上,
故B选项不符合题意;
∵k=<0,
∴当x<0时,y的值随着x的值的增大而增大,
故C选项不符合题意;
∵(x1,y1),(x2,y2)为其函数图象上的两点,且x1x2>0,
∴y1y2=>0,
故D选项符合题意,
故选:D.
【点评】本题考查了反比例函数的图象和性质,熟练掌握反比例函数的性质以及图象上点的坐标特征是解题的关键.
12.(2022秋•石阡县月考)若k>0,则反比例函数的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
【分析】根据反比例函数的图象与系数的关系判断即可.
【解答】解:∵k>0,
∴反比例函数的图象在第一、三象限,
故选:A.
【点评】本题考查了反比例函数的图象,熟练掌握反比例函数的图象与系数的关系是解题的关键.
13.(2021秋•北辰区期末)关于反比例函数的图象性质,下列说法不正确的是( )
A.图象经过点(1,3)
B.图象分别位于第一、三象限
C.图象关于原点对称
D.当x<0时,y随x的增大而增大
【分析】根据反比例函数的性质即可逐一分析找出正确选项.
【解答】解:A.当x=1时,y==3,所以图象经过点(1,3),说法正确,不合题意;
B.k=3>0,则图象位于第一、三象限,故说法正确,不合题意;
C.反比例函数的图象关于原点成中心对称,故说法正确,不合题意;
D.k=3>0,则图象在第一、三象限内,y随x的增大而减小,所以当x>0时,y随x的增大而减小,故说法错误,符合题意;
故选:D.
【点评】本题考查反比例函数的性质,准确理解反比例函数的性质是解题关键,可结合图象更易于分析.
14.(2022•香坊区校级三模)对于反比例函数y=﹣,下列说法不正确的是( )
A.它的图象在第二、四象限
B.点(1,﹣3)在它的图象上
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减少
【分析】根据反比例函数的性质以及反比例函数图象上点的坐标特征判断即可.
【解答】解:A、k=﹣3<0,
∴它的图象在第二、四象限,故本选项正确,不符合题意;
B、∵x=1时,y=﹣=﹣3,
∴点(1,﹣,3)在它的图象上,故本选项正确,不符合题意;
C、k=﹣3<0,当x>0时,y随x的增大而增大,故本选项正确,不符合题意;
D、k=﹣3<0,当x<0时,y随x的增大而增大,故本选项错误,符合题意.
故选:D.
【点评】本题考查了反比例函数的图象和性质,熟练掌握反比例函数的图象和性质是解题的关键.
15.(2022•南京模拟)下列说法正确的是( )
A.函数y=﹣2x的图象是过原点的射线
B.直线y=﹣x+3经过第一、二、三象限
C.函数,y随x增大而增大
D.函数y=2x﹣3,y随x增大而减小
【分析】根据一次函数和反比函数的图象和性质,逐项判断即可求解.
【解答】解:A、函数y=﹣2x的图象是过原点的直线,故本选项错误,不符合题意;
B、因为﹣1<0,3>0,所以直线y=﹣x+3经过第一、二、四象限,故本选项错误,不符合题意;
C、因为﹣3<0,所以函数,y随x增大而增大,故本选项正确,符合题意;
D、因为2>0函数y=2x﹣3,y随x增大而增大,故本选项错误,不符合题意;
故选:C.
【点评】本题主要考查了一次函数和反比函数的图象和性质,熟练掌握一次函数和反比函数的图象和性质是解题的关键.
16.(2022•河南模拟)若双曲线在第二、四象限,那么关于x的方程x2﹣2x+m=0的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.条件不足,无法判断
【分析】由双曲线在第二、四象限,可得出m<0,进而可得出Δ=(﹣2)2﹣4m>0,再利用根的判别式可得出于x的方程x2﹣2x+m=0有两个不相等的实数根.
【解答】解:∵双曲线在第二、四象限,
∴m<0,
∵关于x的方程x2﹣2x+m=0,
∴Δ=(﹣2)2﹣4m>0,
∴关于x的方程x2﹣2x+m=0有两个不相等的实数根.
故选:B.
【点评】本题考查了反比例函数图象与系数的关系以及根的判别式,牢记“k<0⇔y=(k≠0)的图象在二、四象限”是解题的关键.
17.(2021春•盐都区月考)已知反比例函数y=(k≠0)的图象与正比例函数y=mx(m≠0)的图象交于点(2,1),则其另一个交点坐标为 (﹣2,﹣1) .
【分析】根据正比例函数与反比例函数的交点关于原点对称进行解答即可.
【解答】解:∵正比例函数与反比例函数的图象均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(2,1),
∴另一个交点的坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
【点评】本题考查的是正比例函数与反比例函数的交点问题,熟知正比例函数与反比例函数的交点关于原点对称的知识是解答此题的关键.
核心知识2.反比例函数的几何意义
18.(2022•鹿城区校级开学)如图,A为反比例函数y=(k>0)图象上一点,AB⊥x轴于点B,若S△AOB=3,则k的值为( )
A.1.5 B.3 C. D.6
【分析】过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=|k|.
【解答】解:由于点A是反比例函数y=图象上一点,则S△AOB=|k|=3;
又由于k>0,则k=6.
故选:D.
【点评】本题考查了反比例函数系数的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
19.(2022春•丰城市校级期末)如图已知反比例函数的图象如图所示,将该曲线绕点O顺时针旋转45°得到曲线C2,点N是曲线C2上一点,点M在直线y=﹣x上,连接MN、ON,若MN=ON,△MON的面积为,则k的值为( )
A.﹣2 B.﹣4 C. D.
【分析】将直线y=﹣x和曲线C2绕点O逆时针旋转45°,则直线y=﹣x与x轴重合,曲线C2与曲线C1重合,即可求解.
【解答】解:∵将直线y=﹣x和曲线C2绕点O逆时针旋转45°后直线y=﹣x与x轴重合,
∴旋转后点N落在曲线C1上,点M落在x轴上,如图所示,
设点M和点N的对应点分别为点M'和N',
过点N'作N'P⊥x轴于点P,连接ON',M'N',
∵MN=ON,
∴M'N'=ON',M'P=OP,
∴S△MON=2S△PN'O=2×|k|=|k|=2,
∵k<0,
∴k=﹣2.
故选:C.
【点评】本题考查了反比例函数比例系数k的几何意义、旋转的性质,体现了直观想象、逻辑推理的核心素养.
20.(2022春•新野县期末)两个反比例函数C1:和C2:在第一象限内的图象如图所示,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
A.1 B.2 C.3 D.4
【分析】根据反比函数比例系数k的几何意义得到S△AOC=S△BOD=k|,S矩形PCOD=|2|=2,然后利用矩形面积分别减去两个三角形的面积即可得到四边形PAOB的面积.
【解答】解:∵PC⊥x轴,PD⊥y轴,
∴S△AOC=S△BOD=|k|=,S矩形PCOD=|2|=2,
∴四边形PAOB的面积=2﹣2•=1.
故选:A.
【点评】本题考查了反比函数比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
21.(2022春•安溪县期末)如图四个都是反比例函数y=的图象.其中阴影部分面积为6的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据反比例函数系数k的几何意义以及反比例函数的性质判断即可.
【解答】解:第一个的面积为6;第二个的面积为3;第三个的面积为6;第四个的面积为12;
故选:B.
【点评】本题考查了反比例函数系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变;也考查反比例函数的中心对称性.
22.(2022•通辽)如图,点D是▱OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图象经过C,D两点,则k的值是( )
A.﹣6 B.﹣6 C.﹣12 D.﹣12
【分析】过点C作CE⊥y轴,延长BD交CE于点F,易证△COE≌△ABD,求得OE=,根据S△BCD=,求得CF=9,得到点D的纵坐标为4,设C(m,),则D(m+9,4),由反比例函数y=(x<0)的图象经过C,D两点,从而求出m,进而可得k的值.
【解答】解:过点C作CE⊥y轴,延长BD交CE于点F,
∵四边形OABC为平行四边形,
∴AB∥OC,AB=OC,
∴∠COE=∠ABD,
∵BD与y轴平行,
∴∠ADB=90°,
在△COE和△ABD中,
,
∴△COE≌△ABD(AAS),
∴OE=BD=,
∵S△BDC=BD•CF=,
∴CF=9,
∵∠BDC=120°,
∴∠CDF=60°,
∴DF=3,
点D的纵坐标为4,
设C(m,),则D(m+9,4),
∵反比例函数y=(x<0)的图象经过C,D两点,
∴k=m=4(m+9),
∴m=﹣12,
∴k=﹣12,
故选:C.
【点评】本题主要考查反比例函数,掌握平行四边形的性质和反比例函数图象的坐标特征是解题的关键.
23.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )
A.36 B.18 C.12 D.9
【分析】连接AC交BD于E,延长BD交x轴于F,连接OD、OB,设AE=BE=CE=DE=m,D(3,a),根据BD∥y轴,可得B(3,a+2m),A(3+m,a+m),即知k1=3(a+2m)=(3+m)(a+m),从而m=3﹣a,B(3,6﹣a),由B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,得k1=3(6﹣a)=18﹣3a,k2=3a,即得k1+k2=18﹣3a+3a=18.
【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:
∵四边形ABCD是正方形,
∴AE=BE=CE=DE,
设AE=BE=CE=DE=m,D(3,a),
∵BD∥y轴,
∴B(3,a+2m),A(3+m,a+m),
∵A,B都在反比例函数y=(k1>0)的图象上,
∴k1=3(a+2m)=(3+m)(a+m),
∵m≠0,
∴m=3﹣a,
∴B(3,6﹣a),
∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,
∴k1=3(6﹣a)=18﹣3a,k2=3a,
∴k1+k2=18﹣3a+3a=18;
故选:B.
【点评】本题考查反比例函数及应用,涉及正方形性质,解题的关键是用含字母的代数式表示相关点坐标.
24.(2021秋•亳州期末)双曲线C1:y=﹣(k≠0)和C2:y=﹣的图象如图所示,点A是C1上一点,分别过点A作AB⊥x轴,AC⊥y轴,垂足分别为点B、点C,AB与C2交于点D,若△AOD的面积为2,则k的值为( )
A.3 B.5 C.﹣3 D.﹣5
【分析】根据反比例函数k值的几何意义及其基本模型计算即可.
【解答】解:S△AOD=S△AOB﹣S△DOB,
∴,
∴|k|=5,
∵反比例函数位于第二象限,
∴﹣k<0,则k>0,
∴k=5
故选:B.
【点评】本题考查反比例函数k值的几何意义,理解反比例函数k值的几何意义是正确解答关键.
25.(2022•新市区校级一模)如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
A.2 B.4 C.6 D.8
【分析】设A的坐标是(a,0),设B的坐标是(m,n).则mn=k,C的坐标是(,),然后根据C在反比例函数上,则•=k,再根据三角形的面积公式可得an=12,据此即可求解.
【解答】解:设A的坐标是(a,0),设B的坐标是(m,n).则mn=k.
∵C是AB的中点,
∴C的坐标是(,).
∵C在反比例函数上,
∴•=k,即(m+a)n=4k,mn+an=4k.
∵△OAB的面积是6,
∴an=6,即an=12,
∴k+12=4k,
解得k=4.
故选:B.
【点评】本题考查了求反比例函数的解析式,正确设出未知数,转化为k的关系是关键.
26.(2022•钟楼区校级模拟)如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是( )
A.﹣2k1 B.2k2 C.k1+k2 D.k2﹣k1
【分析】先过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,再根据反比例函数系数k的几何意义,求得△ABE的面积=△COD的面积相等=|k2|,△AOE的面积=△CBD的面积相等=|k1|,最后计算平行四边形OABC的面积.
【解答】解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
根据∠AEB=∠CD0=90°,∠ABE=∠COD,AB=CO可得:△ABE≌△COD(AAS),
∴△ABE与△COD的面积相等,
又∵点C在y=的图象上,
∴△ABE的面积=△COD的面积相等=|k2|,
同理可得:△AOE的面积=△CBD的面积相等=|k1|,
∴平行四边形OABC的面积=2(|k2|+|k1|)=|k2|+|k1|=k2﹣k1,
故选:D.
【点评】本题主要考查了反比例函数系数k的几何意义,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.
27.(2022春•锡山区期末)点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,S2+S3=20,则S1的值为 10 .
【分析】根据CD=DE=OE以及反比例函数系数k的几何意义得到S1=k,S四边形OGQD=k,列方程即可得到结论.
【解答】解:∵CD=DE=OE,
∴S1=k,S四边形OGQD=k,
∴S2=(k﹣k×2)=,
S3=k﹣k﹣k=k,
∴k+k=20,
∴k=30,
∴S1=k=10,
故答案为:10.
【点评】本题考查反比例函数系数k的几何意义,矩形的性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
28.(2022春•惠山区期末)如图,四边形OACB是平行四边形,OB在x轴上,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,△AOF的面积为6,则k的值为 8 .
【分析】过F作FM⊥x轴于M,过C作CH⊥x轴于H,得到OD=BH,AD=CH,根据三角形的中位线的性质得到MF=HC=AD,设MF=a,则AD=2a,得到OD=,BM=OD=,根据OM•MF=k,得到k=8.
【解答】解:过F作FM⊥x轴于M,过C作CH⊥x轴于H,
则△ADO≌△CBH,
∴OD=BH,AD=CH,
∵点F为BC的中点,
∴MF=HC=AD,
设MF=a,则AD=2a,
∴OD=,
∴BM=OD=,
∵F在反比例函数的图象上,
∴OM•MF=k,
∴OM=,
∴DB=,
∴S△AOF=S梯形ADMF,
∴(a+2a)••=6,
∴k=8,
故答案为:8.
【点评】本题考查了反比例函数的系数k的几何意义,平行四边形的性质,作出辅助线构建全等三角形是解题的关键.
29.(2022•胶州市二模)如图,两个反比例函数y=和y=在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,若四边形PAOB的面积为5,则k= 8 .
【分析】根据反比例函数系数k的几何意义得到S矩形PCOD=k,S△AOC=S△BOD=,然后利用四边形PAOB的面积=S矩形PCOD﹣S△AOC﹣S△BOD进行计算.
【解答】解:∵PC⊥x轴,PD⊥y轴,∴S矩形PCOD=k,S△AOC=S△BOD==,
∴四边形PAOB的面积=S矩形PCOD﹣S△AOC﹣S△BOD=k﹣﹣=5.解得k=8.故答案是:8.
【点评】主要考查了反比例函数y=中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.
核心知识3.反比例函数与一次函数
30.(2022•攀枝花)如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x≤时,x的取值范围是( )
A.﹣1≤x<0或x≥1 B.x≤﹣1或0<x≤1
C.x≤﹣1或x≥1 D.﹣1≤x<0或0<x≤1
【分析】根据反比例函数的对称性求得B点的坐标,然后根据图象即可求得.
【解答】解:∵正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,
∴B(﹣1,﹣m),
由图象可知,当k1x≤时,x的取值范围是﹣1≤x<0或x≥1,
故选:A.
【点评】本题考查了反比例函数与一次函数的交点问题,利用函数的对称性求得B点的坐标,以及数形结合思想的运用是解题的关键.
31.(2022•宝安区校级模拟)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m为常数且m≠0)的图象都经过A(﹣1,2),B(2,﹣1),结合图象,则不等式kx>﹣b的解集是( )
A.x<﹣1 B.﹣1<x<0
C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
【分析】根据一次函数图象在反比例函数图象上方的x的取值范围便是不等式kx>﹣b的解集.
【解答】解:由函数图象可知,当一次函数y1=kx+b(k≠0)的图象在反比例函数y2=(m为常数且m≠0)的图象上方时,x的取值范围是:x<﹣1或0<x<2,
∴不等式kx>﹣b的解集是x<﹣1或0<x<2,
故选:C.
【点评】本题是一次函数图象与反比例函数图象的交点问题:主要考查了由函数图象求不等式的解集.利用数形结合是解题的关键.
32.(2022•普陀区校级开学)如图,一次函数y1=kx+b的图象与反比例函数的图象相交于点A(,4)和点B(3,n).若y1<y2,则x的取值范围是( )
A.x<0或<x<3 B.x<或x>3
C.0<x<或x>3 D.x<0或x>3
【分析】根据一次函数与反比例函数交点坐标,结合图象确定出所求x的范围即可.
【解答】解:根据图象得:当y1<y2时,x的取值范围是0<x<或x>3,
故选:C.
【点评】此题考查了反比例函数与一次函数的交点问题,利用了数形结合的思想,弄清数形结合思想是解本题的关键.
33.(2022春•德化县期中)如图,在平面直角坐标系中,直线y=mx(m≠0,m为常数)与双曲线(k≠0,k为常数)交于点A,B,若A(﹣1,a),B(b,﹣3),过点A作AM⊥x轴,垂足为M,连接BM,则△ABM的面积是( )
A.2 B.m﹣1 C.3 D.6
【分析】根据反比例的图象关于原点中心对称得到点A与点B关于原点中心对称,则S△OAM=S△OBM,A(﹣1,3),(1,﹣3),代入解析式求得k=﹣3,然后根据反比例函数y=(k≠0)系数k的几何意义即可得到S△AOM=|k|=,进一步得出S△ABM=2S△AOM=3.
【解答】解:∵直线y=mx(m≠0,m为常数)与双曲线(k≠0,k为常数)交于点A,B,
∴点A与点B关于原点中心对称,
∴S△OAM=S△OBM,
∵A(﹣1,a),B(b,﹣3),
∴a=3,b=1,
∴A(﹣1,3),(1,﹣3),
∴k=﹣1×3=﹣3,
∵AM⊥x轴,垂足为M,
∴S△AOM=|k|=,
∵S△OAM=S△OBM,
∴S△ABM=2S△AOM=3,
故选:C.
【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
34.(2021秋•东港区校级月考)如图,一次函数y=2x与反比例函数y=的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为,则k的值为( )
A. B. C. D.
【分析】作辅助线,先确定OQ长的最小时点P的位置,当BP延长线过圆心C时,BP最短,设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,根据勾股定理计算t的值,可得k的值.
【解答】解:连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=BP,
∵OQ长的最小值为,
∴BP长的最小值为×2=1,
如图,当BP的延长线过圆心C时,BP最短,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴22=(t+2)2+(﹣2t)2,
解得t=0(舍)或﹣,
∴B(﹣,﹣),
∵点B在反比例函数y=(k>0)的图象上,
∴k=﹣×(﹣)=;
故选:C.
【点评】本题考查了反比例函数与一次函数的交点问题、圆的性质,勾股定理的应用,有难度,解题的关键:利用勾股定理建立方程解决问题.
35.(2022•渠县一模)如图,直线y=ax+b与函数y=(x>0)的图象交于A(1,m)、B(n,1)两点,与x轴交于点C,且,则不等式ax+b>的解集在数轴上表示正确的是( )
A. B.
C. D.
【分析】作AD⊥x轴于D,BE⊥x轴于E,则AD∥BE,根据平行线分线段成比例定理求得m=3,即可求得A(1,3),根据反比例函数系数k=xy得到k=1×3=n•1,求得n=3,即B(3,1),观察图象即可得到不等式ax+b>的解集.
【解答】解:作AD⊥x轴于D,BE⊥x轴于E,则AD∥BE,
∴==,
∵A(1,m)、B(n,1),
∴AD=m,BE=1,
∴m=3,
∴A(1,3),
∵函数y=(x>0)的图象国过点A(1,3)、B(n,1)两点,
∴k=1×3=n•1,
∴n=3,
∴B(3,1),
观察图象,不等式ax+b>的解集为1<x<3,
故选:D.
【点评】本题是反比例函数与一次函数的交点问题,考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,函数与不等式的关系,求得B点的坐标、数形结合是解题的关键.
36.(2022•江汉区校级模拟)若一次函数y=kx+b和反比例函数y=(m<0)的图象交于点A(﹣3,y1),B(1,y2),则不等式kx2+bx﹣m<0的解集是( )
A.x>1或x<﹣3 B.0<x<1或x<﹣3
C.﹣3<x<0或x>1 D.﹣3<x<0或0<x<1
【分析】分两种情况讨论,观察一次函数y=kx+b(k≠0)图象和反比例函数y=(m<0)的图象,即可求得x的取值范围.
【解答】解:∵m<0,
∴反比例函数y=(m<0)的图象在第二、四象限,如图,
当x>0时,
∵kx2+bx﹣m<0,
∴kx+b<,
由函数图象可知,当一次函数y=kx+b(k≠0)图象在反比例函数y=(m<0)的图象下方时,x的取值范围是:x>1,
当x<0时,
∵kx2+bx﹣m<0,
∴kx+b>,
由函数图象可知,当一次函数y=kx+b(k≠0)图象在反比例函数y=(m<0)的图象上方时,x的取值范围是:x<﹣3,
∴等式kx2+bx﹣m<0的解集是:x>1或x<﹣3,
故选:A.
【点评】本题是一次函数图象与反比例函数图象的交点问题:主要考查了由函数图象求不等式的解集.利用数形结合是解题的关键.
核心知识4.待定系数法反比例函数解析式
37.(2022秋•冷水滩区校级月考)反比例函数的图象过点A(2,﹣8).
(1)求这个函数的表达式;
(2)请判断点B(﹣4,4)是否是这个反比例函数的图象上,并说明理由.
【分析】(1)把点A(2,﹣8)直接代入反比例函数,求得函数解析式即可;
(2)把点B(﹣4,4)代入(1)中的函数解析式,判断即可.
【解答】解:(1)∵反比例函数的图象过点A(2,﹣8).
∴k=2×(﹣8)=﹣16,
所以反比例函数的解析式为y=﹣;
(2)把x=﹣4代入y=﹣得,y=4,
∴点B(﹣4,4)在这个反比例函数的图象上.
【点评】此题考查待定系数法求函数解析式,反比例函数图象上点的坐标体系,将点的坐标代入解析式,利用方程解决问题.
38.(2022秋•娄星区校级月考)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(﹣3,n),B(2,3).
(1)求反比例函数与一次函数的函数表达式;
(2)请结合图象直接写出不等式kx+b≥的解集;
(3)若点P为x轴上一点,△ABP的面积为10,直接写出点P的坐标.
【分析】(1)根据反比例函数y=的图象经过B(2,3),利用待定系数法即可求出反比例函数的解析式;进而求得A的坐标,根据A、B点坐标,进而利用待定系数法求出一次函数解析式;
(2)根据A、B的坐标,结合图象即可求得;
(3)根据三角形面积求出CP的长,根据C的坐标即可得出P的坐标.
【解答】解:(1)∵反比例函数y=的图象经过B(2,3),
∴m=2×3=6.
∴反比例函数的解析式为y=.
∵A(﹣3,n)在y=上,所以n=﹣2.
∴A的坐标是(﹣3,﹣2).
把A(﹣3,﹣2)、B(2,3)代入y=kx+b.得,
解得,
∴一次函数的解析式为y=x+1.
(2)由图象可知:不等式kx+b≥的解集是﹣3≤x<0或x≥2;
(3)把y=0代入y=x+1得:0=x+1,
∴x=﹣1,
∴C的坐标是(﹣1,0),
∵P为x轴上一点,且△ABP的面积为10,A(﹣3,﹣2),B(2,3),
∴CP×2+CP×3=10,
∴CP=4,
∴当P在负半轴上时,P的坐标是(﹣5,0);
当P在正半轴上时,P的坐标是(3,0),
即P的坐标是(﹣5,0)或(3,0).
【点评】本题考查了用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,三角形的面积的应用,主要考查学生的计算能力.
39.(2022•微山县二模)如图,正方形OABC在平面直角坐标系中,点B的坐标是(2,2),顶点A,C在坐标轴上,反比例函数在第一象限的图象分别交AB,AC于点E,F,连接OF,EC交于点M,△OFC的面积等于1.
(1)求反比例函数的解析式;
(2)求四边形OAEM的面积.
【分析】(1)利用反比例函数系数k的几何意义即可求得;
(2)求得E、F的坐标,即可求得直线OF为y=x,直线EC为y=﹣2x+4,两直线解析式联立成方程组,解方程求得M点的坐标,然后根据四边形OAEM的面积=S正方形OABC﹣S△BCE﹣S△OCM求得即可.
【解答】解:(1)∵正方形OABC在平面直角坐标系中,顶点A,C在坐标轴上,
∴BC⊥x轴,
∴S△OFC=k=1,
∴k=2,
∴反比例函数的解析式为y=;
(2)∵B(2,2),
∴E点的纵坐标为2,F的横坐标为2,
∴E(1,2),F(2,1),
∴直线OF为y=x,直线EC为y=﹣2x+4,
解得,
∴M(,),
∴四边形OAEM的面积=S正方形OABC﹣S△BCE﹣S△OCM=2×2﹣×1×2﹣=.
【点评】本题考查了反比例函数系数k的几何意义,正方形的性质,反比例函数图象上点的坐标特征,利用分割法求得四边形的面积是解题的关键.
40.(2022•咸丰县模拟)如图,平面直角坐标系xOy中,函数的图象上A、B两点的坐标分别为A(n,n+1),B(n﹣5,﹣2n).
(1)求反比例函数和直线AB的解析式;
(2)连接AO、BO,求△AOB的面积.
【分析】(1)根据反比例函数系数k=xy得出n(n+1)=(n﹣5)(﹣2n),即n2+n=﹣2n2+10n3n2﹣9n=0,解方程求得A、B的坐标,进而即可利用待定系数法求得函数的解析式;
(2)求得D的坐标,然后利用三角形面积公式即可求得.
【解答】解:(1)∵A、B两点在的图象上,而A(n,n+1),B(n﹣5,﹣2n),
∴n(n+1)=(n﹣5)(﹣2n),即n2+n=﹣2n2+10n3n2﹣9n=0,
解得n1=0,n2=3
∵的图象与坐标轴没有交点,
∴n1=0舍去,
∴n=3,
∴A(3,4),B(﹣2,﹣6),
∴k=3×4=12,
设直线AB的解析式为:y=ax+b,
则,
解得:
∴直线AB的解析式为:y=2x﹣2,反比例函数解析式为:;
(2)设直线AB交x轴于点D,则
当y=0时,2x﹣2=0,
∴x=1,
∴D(1,0),
∴
∴△AOB的面积为5.
【点评】本题考查了待定系数法求反比例函数的解析式,一次函数的解析式,一次函数图象上点的坐标特征,三角形的面积,求得A、B点的坐标是解题的关键.
41.(2021秋•霸州市期末)如图,直线l:y=﹣x+4与x轴、y轴分别交于点A,B,点P,Q均在l上,点P的横坐标为m,点Q的横坐标为m+1,反比例函数(k>0,x>0)的图象L经过点P.
(1)若m=1,
①求L的解析式;
②判断L是否经过点Q,并说明理由.
(2)若L经过点Q,求m的值.
【分析】(1)①把x=1代入y=﹣x+4得,y=3,求得P(1,3),代入(k>0,x>0)即可得到结论;
②把x=2代入y=﹣x+4得到Q(2,2),由于2×2=4≠3,于是得到结论;
(2)根据题意得方程即可得到结论.
【解答】解:(1)①把x=1代入y=﹣x+4得,y=3,
∴P(1,3),
∵反比例函数(k>0,x>0)的图象L经过点P,
∴k=1×3=3,
∴L的解析式为y=;
②L不经过点Q,
理由:∵m=1,
∴点Q的横坐标为2,
把x=2代入y=﹣x+4得,y=2,
∴Q(2,2),
∵2×2=4≠3,
∴L不经过点Q;
(2)∵点P,Q均在l上,点P的横坐标为m,点Q的横坐标为m+1,
∴Q(m+1,﹣m+3),P(m,﹣m+4)
∵L经过点Q,点P,
∴(m+1)(﹣m+3)=m(﹣m+4),
解得m=.
【点评】本题考查了待定系数法求反比例函数的解析式,一次函数的性质,反比例函数点的坐标特征,正确地求得反比例函数的解析式是解题的关键.
核心知识5.反比例函数的应用
42.(2022•南京模拟)在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(4,3)在其图象上,则当力达到10N时,物体在力的方向上移动的距离是( )
A.2.4m B.1.2m C.1m D.0.5m
【分析】利用点P的坐标求出F=,当F=10时,即F==10,求出s,即可求解.
【解答】解:设函数的表达式F=,
将点P的坐标代入上式得:3=,
解得k=12,
则反比例函数表达式为F=,
当F=10时,即F==10,
解得s=1.2,
故选:B.
【点评】本题考查反比例函数的应用,用待定系数法求反比例函数解析式是解题关键.
43.(2022•宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
【分析】由油箱中油的体积V与电路中总电阻R总是反比例关系,电流I与R总是反比例关系,可得V=I(为常数),即可得到答案.
【解答】解:由油箱中油的体积V与电路中总电阻R总是反比例关系,设V•R总=k(k为常数),
由电流I与R总是反比例关系,设I•R总=k'(k为常数),
∴=,
∴V=I(为常数),
∴I与V的函数关系是正比例函数,
故选:B.
【点评】本题考查反比例函数与正比例函数的应用,解题的关键是掌握反比例函数与正比例函数的概念.
44.(2022春•无锡期末)古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N和0.5m,小明最多能使出500N的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )
A.至多为1.6m B.至少为1.6m
C.至多为0.625m D.至少为0.625m
【分析】直接利用:阻力×阻力臂=动力×动力臂,进而得出F与l之间的函数表达式;把F=500N代入所求的函数解析式即可得到结论.
【解答】解:由题意可得:1600×0.5=Fl,
则F与l的函数表达式为:F=;
当动力F=500N时,
500=,
解得l=,
答:动力F=500N时,动力臂至少为1.6m,
故选:B.
【点评】此题主要考查了反比例函数的应用,正确得出F与l之间的关系是解题关键.
45.(2022•大同三模)如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当R<0.25时,I<880
B.I与R的函数关系式是I=(R>0)
C.当R>1000时,I>0.22
D.当880<R<1000时,I的取值范围是0.22<I<0.25
【分析】由待定系数法求出反比例函数的解析式,根据反比例函数的性质逐项分析即可得到结论.
【解答】解:设I与R的函数关系式是I=(R>0),
∵该图象经过点P(880,0.25),
∴=0.25,
∴U=220,
∴I与R的函数关系式是I=(R>0),故选项B不符合题意;
当R=0.25时,I=880,当R=1000时,I=0.22,
∵反比例函数I=(R>0)I随R的增大而减小,
当R<0.25时,I>880,当R>1000时,I<0.22,故选项A,C不符合题意;
∵R=0.25时,I=880,当R=1000时,I=0.22,
∴当880<R<1000时,I的取值范围是0.22<I<0.25,故D符合题意;
故选:D.
【点评】本题主要考查了反比例函数的应用,由待定系数法求出反比例函数的解析式是解决问题的关键.
46.(2022秋•东平县校级月考)当下教育主管部门提倡加强高效课堂建设,要求教师课堂上要精讲,把时间、思考、课堂还给学生.通过实验发现:学生在课堂上听课注意力指标随上课时间的变化而变化,上课开始后,学生的学习兴趣递增,中间一段时间,学生的兴趣保持平稳高效状态,后阶段注意力开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段,当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值.
(2)如果学生在课堂上的注意力指标不低于30属于学习高效阶段,请你求出学生在课堂上的学习高效时间段.
【分析】(1)设反比例函数的解析式为y=,由C(20,45)求出k,可得D坐标,从而求出A的指标值;
(2)求出AB解析式,得到y≥30时x≥4,由反比例函数y=可得y≥30时,x≤30,即可得到答案.
【解答】解:(1)设当20≤x≤45时,反比例函数的解析式为y=,
将C(20,45)代入得:45=,
解得k=900,
∴反比例函数的解析式为y=,
当x=45时,y==20,
∴D(45,20),
∴A(0,20),即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
,
解得,
∴AB的解析式为y=x+20,
当y≥30时,x+20≥30,
解得x≥4,
由(1)得反比例函数的解析式为y=,
当y≥30时,≥30,
解得x≤30,
∴4≤x≤30时,注意力指标都不低于30.
【点评】本题考查函数图象的应用,涉及一次函数、反比例函数及不等式等知识,解题的关键是求出0≤x<10和20≤x≤45时的解析式.
47.(2022秋•荣成市校级月考)疫情防控期间,某校校医每天早上对全校办公室和教室进行药物喷洒消毒,完成一间办公室和一间教室的喷洒共需8min;完成两间办公室和三间教室的喷洒共需21min.消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示.进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,后勤人员依次对一班至十一班教室(共11间)进行药物喷洒消毒,当最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
【分析】设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,根据题意列方程组可得一间教室的药物喷洒时间为5min,即可根据点A在y=2x上,求出点A的坐标(5,10),从而得反比例函数表达式为y=,当x=55时,y=<1,即可作出判断.
【解答】解:设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,
则,
解得,
∴一间教室的药物喷洒时间为5min,
∴11个教室需要55min,
当x=5时,y=2x=10,故点A(5,10),
设反比例函数表达式为:y=,将点A的坐标代入上式可解得:k=50,
∴反比例函数表达式为y=,
当x=55时,y=<1,
∴一班学生能安全进入教室.
【点评】本题主要考查反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
班级 姓名 学号 分数
第二十六章 反比例函数(A卷·知识通关练)
核心知识1反比例函数图像与性质
1.(2022秋•定远县校级月考)下列函数:①y=x﹣2②y=﹣③y=﹣1④y=,y是x的反比例函数的个数有( )
A.0个 B.1个 C.2个 D.3个
【分析】利用反比例函数定义进行解答即可.
【解答】解:①是一次函数,不是反比例函数;
②是反比例函数;
③不是反比例函数;
④不是反比例函数;
共1个,
故选:B.
【点评】此题主要考查了反比例函数的定义,判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y=(k为常数,k≠0)或y=kx﹣1(k为常数,k≠0).
2.(2022秋•东平县校级月考)函数y=和y=kx﹣k(k≠0)在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
【分析】分别根据反比例函数及一次函数图象的特点对四个选项进行逐一分析即可.
【解答】解:由反比例函数y=的图象在一、三象限可知,﹣k>0,∴k<0,∴一次函数y=kx﹣k的图象经过一、二、四象限,故A、C选项错误,B选项正确;
由反比例函数y=的图象在二、四象限可知,﹣k<0,∴k>0,∴一次函数y=kx﹣k的图象经过一、三、四象限,故D选项错误;
故选:B.
【点评】本题考查的是反比例函数及一次函数图象,解答此题的关键是先根据反比例函数所在的象限判断出k的符号,再根据一次函数的性质进行解答.
3.(2022•襄阳)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【分析】根据二次函数图象开口向下得到a<0,再根据对称轴确定出b,根据与y轴的交点确定出c<0,然后确定出一次函数图象与反比例函数图象的情况,即可得解.
【解答】解:∵二次函数图象开口方向向下,
∴a<0,
∵对称轴为直线x=﹣>0,
∴b>0,
∵与y轴的负半轴相交,
∴c<0,
∴y=bx+c的图象经过第一、三、四象限,
反比例函数y=图象在第二四象限,
只有D选项图象符合.
故选:D.
【点评】本题考查了二次函数的图形,一次函数的图象,反比例函数的图象,熟练掌握二次函数的有关性质:开口方向、对称轴、与y轴的交点坐标等确定出a、b、c的情况是解题的关键.
4.(2022•菏泽)根据如图所示的二次函数y=ax2+bx+c的图象,判断反比例函数y=与一次函数y=bx+c的图象大致是( )
A. B. C. D.
【分析】先根据二次函数的图象,确定a、b、c的符号,再根据a、b、c的符号判断反比例函数y=与一次函数y=bx+c的图象经过的象限即可.
【解答】解:由二次函数图象可知a>0,c<0,
由对称轴x=﹣>0,可知b<0,
所以反比例函数y=的图象在一、三象限,一次函数y=bx+c图象经过二、三、四象限.
故选:A.
【点评】本题主要考查二次函数图象的性质、一次函数的图象的性质、反比例函数图象的性质,关键在于通过二次函数图象推出a、b、c的取值范围.
5.(2022•安顺)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b和反比例函数y=(c≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
【分析】直接利用二次函数图象经过的象限得出a,b,c的取值范围,进而利用一次函数与反比例函数的性质得出答案.
【解答】解:∵二次函数y=ax2+bx+c的图象开口向上,
∴a>0,
∵该抛物线对称轴位于y轴的右侧,
∴a、b异号,即b<0.
∵抛物线交y轴的负半轴,
∴c<0,
∴一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=(c≠0)在二、四象限.
故选:A.
【点评】此题主要考查了反比例函数、一次函数、二次函数的图象,正确把握相关性质是解题关键.
6.(2022春•钱塘区期末)描点法是画未知函数图象的常用方法.请判断函数的图象可能为( )
A. B.
C. D.
【分析】根据反比例函数的性质可知函数y=在第一、三象限,对称中心为原点,根据函数平移的规律,把y=向左平移1个单位得到y=,对称中心为(﹣1,0),据此即可判断.
【解答】解:∵k=1,
∴函数y=在第一、三象限,对称中心为原点,
把y=向左平移1个单位得到y=,对称中心为(﹣1,0),
故选:D.
【点评】本题考查了反比例函数的图象和性质,函数y=与函数y=的关系是解题的关键.
7.(2022•崂山区二模)已知一次函数y=abx+bc的图象如图所示,则二次函数y=ax2+bx+c和反比例函数y=在同一坐标系内的图象可能是( )
A. B.
C. D.
【分析】根据一次函数的图象所经过的象限可以判定a、b、c的符号,从而得到ab<0,bc>0,然后根据二次函数和反比例函数经过的象限,判定a、b、c的符号,从而得出ab和bc的符号,看是否一致.
【解答】解:∵一次函数y=abx+bc的图象经过第一、二、四象限,
∴ab<0,bc>0.
∴反比例函数y=经过第二、四象限,故A、C不合题意,B、D符合题意;
B、二次函数y=ax2+bx+c图象开口向上,对称轴为y轴,交y的负半轴,
∴a>0,b=0,c<0,
∴ab=0,bc=0,故B不合题意;
D、二次函数y=ax2+bx+c图象开口向下,对称轴在y轴右,交y的正半轴,
∴a<0,b>0,c>0,
∴ab<0,bc>0,故D符合题意;
故选:D.
【点评】本题考查了二次函数图象,一次函数图象,反比例函数图象,根据二次函数图象判断出a、b、c的符号情况是解题的关键.
8.(2022•平泉市一模)如图,把函数y=(x>0)和函数y=﹣(x>0)的图象画在同一平面直角坐标系中,则坐标系的横轴可能是( )
A.l1 B.l2 C.l3 D.l4
【分析】根据反比例函数k的取值分析即可.
【解答】解:在函数y=(x>0)和函数y=﹣(x>0)中,
∵2>0,﹣4<0,
∴函数y=(x>0)的图象在第一象限,函数y=﹣(x>0)的图象在第四象限,
∵|﹣4|>|2|,
∴y=(x>0)的图象更靠近坐标轴,
∴坐标系的横轴可以是l2,
故选:B.
【点评】本题考查了反比例函数的图象,熟练掌握反比例函数的性质是解题的关键.
9.(2021秋•房县期末)如图,点P(﹣2a,a)是反比例函数y=的图象与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
【分析】根据圆的对称性以及反比例函数的对称性可得,阴影部分的面积等于圆的面积,即可求得圆的半径,再根据P在反比例函数的图象上,以及在圆上,即可求得k的值.
【解答】解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π.
解得:r=2.
∵点P(﹣2a,a)是反比例函数y=(k<0)与⊙O的一个交点.
∴﹣2a2=k且=r.
∴a2=8.
∴k=﹣2×8=﹣16,
则反比例函数的解析式是:y=﹣.
故选:D.
【点评】本题主要考查反比例函数图象的对称性的知识点,解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系.
10.(2021秋•龙泉驿区期中)如图,过原点的一条直线与反比例函数(k≠0)的图象分别交于A、B两点,若A点的坐标为(3,﹣5),则B点的坐标为( )
A.(3,﹣5) B.(﹣5,3) C.(﹣3,+5) D.(+3,﹣5)
【分析】根据关于原点对称的两点横坐标,纵坐标都互为相反数即可解答.
【解答】解:∵反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称,
∴它的另一个交点的坐标是(﹣3,+5).
故选:C.
【点评】此题考查了反比例函数图象的对称性.反比例函数的图象关于原点对称.
11.(2022秋•石阡县月考)对于反比例函数的叙述错误的是( )
A.其图象关于原点对称
B.点在其图像上
C.当x<0时,y的值随x的值的增大而增大
D.若(x1,y1),(x2,y2)为其函数图象上的两点,且x1x2>0,则y1y2<0
【分析】根据反比例函数的图象和性质,以及反比例函数图象上点的坐标特征依次进行判断即可.
【解答】解:∵反比例函数的图象是中心对称图形,
∴其图象关于原点对称,
故A选项不符合题意;
当x=时,y=﹣1,
∴点A(,﹣1)在其图象上,
故B选项不符合题意;
∵k=<0,
∴当x<0时,y的值随着x的值的增大而增大,
故C选项不符合题意;
∵(x1,y1),(x2,y2)为其函数图象上的两点,且x1x2>0,
∴y1y2=>0,
故D选项符合题意,
故选:D.
【点评】本题考查了反比例函数的图象和性质,熟练掌握反比例函数的性质以及图象上点的坐标特征是解题的关键.
12.(2022秋•石阡县月考)若k>0,则反比例函数的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
【分析】根据反比例函数的图象与系数的关系判断即可.
【解答】解:∵k>0,
∴反比例函数的图象在第一、三象限,
故选:A.
【点评】本题考查了反比例函数的图象,熟练掌握反比例函数的图象与系数的关系是解题的关键.
13.(2021秋•北辰区期末)关于反比例函数的图象性质,下列说法不正确的是( )
A.图象经过点(1,3)
B.图象分别位于第一、三象限
C.图象关于原点对称
D.当x<0时,y随x的增大而增大
【分析】根据反比例函数的性质即可逐一分析找出正确选项.
【解答】解:A.当x=1时,y==3,所以图象经过点(1,3),说法正确,不合题意;
B.k=3>0,则图象位于第一、三象限,故说法正确,不合题意;
C.反比例函数的图象关于原点成中心对称,故说法正确,不合题意;
D.k=3>0,则图象在第一、三象限内,y随x的增大而减小,所以当x>0时,y随x的增大而减小,故说法错误,符合题意;
故选:D.
【点评】本题考查反比例函数的性质,准确理解反比例函数的性质是解题关键,可结合图象更易于分析.
14.(2022•香坊区校级三模)对于反比例函数y=﹣,下列说法不正确的是( )
A.它的图象在第二、四象限
B.点(1,﹣3)在它的图象上
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减少
【分析】根据反比例函数的性质以及反比例函数图象上点的坐标特征判断即可.
【解答】解:A、k=﹣3<0,
∴它的图象在第二、四象限,故本选项正确,不符合题意;
B、∵x=1时,y=﹣=﹣3,
∴点(1,﹣,3)在它的图象上,故本选项正确,不符合题意;
C、k=﹣3<0,当x>0时,y随x的增大而增大,故本选项正确,不符合题意;
D、k=﹣3<0,当x<0时,y随x的增大而增大,故本选项错误,符合题意.
故选:D.
【点评】本题考查了反比例函数的图象和性质,熟练掌握反比例函数的图象和性质是解题的关键.
15.(2022•南京模拟)下列说法正确的是( )
A.函数y=﹣2x的图象是过原点的射线
B.直线y=﹣x+3经过第一、二、三象限
C.函数,y随x增大而增大
D.函数y=2x﹣3,y随x增大而减小
【分析】根据一次函数和反比函数的图象和性质,逐项判断即可求解.
【解答】解:A、函数y=﹣2x的图象是过原点的直线,故本选项错误,不符合题意;
B、因为﹣1<0,3>0,所以直线y=﹣x+3经过第一、二、四象限,故本选项错误,不符合题意;
C、因为﹣3<0,所以函数,y随x增大而增大,故本选项正确,符合题意;
D、因为2>0函数y=2x﹣3,y随x增大而增大,故本选项错误,不符合题意;
故选:C.
【点评】本题主要考查了一次函数和反比函数的图象和性质,熟练掌握一次函数和反比函数的图象和性质是解题的关键.
16.(2022•河南模拟)若双曲线在第二、四象限,那么关于x的方程x2﹣2x+m=0的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.条件不足,无法判断
【分析】由双曲线在第二、四象限,可得出m<0,进而可得出Δ=(﹣2)2﹣4m>0,再利用根的判别式可得出于x的方程x2﹣2x+m=0有两个不相等的实数根.
【解答】解:∵双曲线在第二、四象限,
∴m<0,
∵关于x的方程x2﹣2x+m=0,
∴Δ=(﹣2)2﹣4m>0,
∴关于x的方程x2﹣2x+m=0有两个不相等的实数根.
故选:B.
【点评】本题考查了反比例函数图象与系数的关系以及根的判别式,牢记“k<0⇔y=(k≠0)的图象在二、四象限”是解题的关键.
17.(2021春•盐都区月考)已知反比例函数y=(k≠0)的图象与正比例函数y=mx(m≠0)的图象交于点(2,1),则其另一个交点坐标为 (﹣2,﹣1) .
【分析】根据正比例函数与反比例函数的交点关于原点对称进行解答即可.
【解答】解:∵正比例函数与反比例函数的图象均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(2,1),
∴另一个交点的坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
【点评】本题考查的是正比例函数与反比例函数的交点问题,熟知正比例函数与反比例函数的交点关于原点对称的知识是解答此题的关键.
核心知识2.反比例函数的几何意义
18.(2022•鹿城区校级开学)如图,A为反比例函数y=(k>0)图象上一点,AB⊥x轴于点B,若S△AOB=3,则k的值为( )
A.1.5 B.3 C. D.6
【分析】过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=|k|.
【解答】解:由于点A是反比例函数y=图象上一点,则S△AOB=|k|=3;
又由于k>0,则k=6.
故选:D.
【点评】本题考查了反比例函数系数的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
19.(2022春•丰城市校级期末)如图已知反比例函数的图象如图所示,将该曲线绕点O顺时针旋转45°得到曲线C2,点N是曲线C2上一点,点M在直线y=﹣x上,连接MN、ON,若MN=ON,△MON的面积为,则k的值为( )
A.﹣2 B.﹣4 C. D.
【分析】将直线y=﹣x和曲线C2绕点O逆时针旋转45°,则直线y=﹣x与x轴重合,曲线C2与曲线C1重合,即可求解.
【解答】解:∵将直线y=﹣x和曲线C2绕点O逆时针旋转45°后直线y=﹣x与x轴重合,
∴旋转后点N落在曲线C1上,点M落在x轴上,如图所示,
设点M和点N的对应点分别为点M'和N',
过点N'作N'P⊥x轴于点P,连接ON',M'N',
∵MN=ON,
∴M'N'=ON',M'P=OP,
∴S△MON=2S△PN'O=2×|k|=|k|=2,
∵k<0,
∴k=﹣2.
故选:C.
【点评】本题考查了反比例函数比例系数k的几何意义、旋转的性质,体现了直观想象、逻辑推理的核心素养.
20.(2022春•新野县期末)两个反比例函数C1:和C2:在第一象限内的图象如图所示,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
A.1 B.2 C.3 D.4
【分析】根据反比函数比例系数k的几何意义得到S△AOC=S△BOD=k|,S矩形PCOD=|2|=2,然后利用矩形面积分别减去两个三角形的面积即可得到四边形PAOB的面积.
【解答】解:∵PC⊥x轴,PD⊥y轴,
∴S△AOC=S△BOD=|k|=,S矩形PCOD=|2|=2,
∴四边形PAOB的面积=2﹣2•=1.
故选:A.
【点评】本题考查了反比函数比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
21.(2022春•安溪县期末)如图四个都是反比例函数y=的图象.其中阴影部分面积为6的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据反比例函数系数k的几何意义以及反比例函数的性质判断即可.
【解答】解:第一个的面积为6;第二个的面积为3;第三个的面积为6;第四个的面积为12;
故选:B.
【点评】本题考查了反比例函数系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变;也考查反比例函数的中心对称性.
22.(2022•通辽)如图,点D是▱OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图象经过C,D两点,则k的值是( )
A.﹣6 B.﹣6 C.﹣12 D.﹣12
【分析】过点C作CE⊥y轴,延长BD交CE于点F,易证△COE≌△ABD,求得OE=,根据S△BCD=,求得CF=9,得到点D的纵坐标为4,设C(m,),则D(m+9,4),由反比例函数y=(x<0)的图象经过C,D两点,从而求出m,进而可得k的值.
【解答】解:过点C作CE⊥y轴,延长BD交CE于点F,
∵四边形OABC为平行四边形,
∴AB∥OC,AB=OC,
∴∠COE=∠ABD,
∵BD与y轴平行,
∴∠ADB=90°,
在△COE和△ABD中,
,
∴△COE≌△ABD(AAS),
∴OE=BD=,
∵S△BDC=BD•CF=,
∴CF=9,
∵∠BDC=120°,
∴∠CDF=60°,
∴DF=3,
点D的纵坐标为4,
设C(m,),则D(m+9,4),
∵反比例函数y=(x<0)的图象经过C,D两点,
∴k=m=4(m+9),
∴m=﹣12,
∴k=﹣12,
故选:C.
【点评】本题主要考查反比例函数,掌握平行四边形的性质和反比例函数图象的坐标特征是解题的关键.
23.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )
A.36 B.18 C.12 D.9
【分析】连接AC交BD于E,延长BD交x轴于F,连接OD、OB,设AE=BE=CE=DE=m,D(3,a),根据BD∥y轴,可得B(3,a+2m),A(3+m,a+m),即知k1=3(a+2m)=(3+m)(a+m),从而m=3﹣a,B(3,6﹣a),由B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,得k1=3(6﹣a)=18﹣3a,k2=3a,即得k1+k2=18﹣3a+3a=18.
【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:
∵四边形ABCD是正方形,
∴AE=BE=CE=DE,
设AE=BE=CE=DE=m,D(3,a),
∵BD∥y轴,
∴B(3,a+2m),A(3+m,a+m),
∵A,B都在反比例函数y=(k1>0)的图象上,
∴k1=3(a+2m)=(3+m)(a+m),
∵m≠0,
∴m=3﹣a,
∴B(3,6﹣a),
∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,
∴k1=3(6﹣a)=18﹣3a,k2=3a,
∴k1+k2=18﹣3a+3a=18;
故选:B.
【点评】本题考查反比例函数及应用,涉及正方形性质,解题的关键是用含字母的代数式表示相关点坐标.
24.(2021秋•亳州期末)双曲线C1:y=﹣(k≠0)和C2:y=﹣的图象如图所示,点A是C1上一点,分别过点A作AB⊥x轴,AC⊥y轴,垂足分别为点B、点C,AB与C2交于点D,若△AOD的面积为2,则k的值为( )
A.3 B.5 C.﹣3 D.﹣5
【分析】根据反比例函数k值的几何意义及其基本模型计算即可.
【解答】解:S△AOD=S△AOB﹣S△DOB,
∴,
∴|k|=5,
∵反比例函数位于第二象限,
∴﹣k<0,则k>0,
∴k=5
故选:B.
【点评】本题考查反比例函数k值的几何意义,理解反比例函数k值的几何意义是正确解答关键.
25.(2022•新市区校级一模)如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
A.2 B.4 C.6 D.8
【分析】设A的坐标是(a,0),设B的坐标是(m,n).则mn=k,C的坐标是(,),然后根据C在反比例函数上,则•=k,再根据三角形的面积公式可得an=12,据此即可求解.
【解答】解:设A的坐标是(a,0),设B的坐标是(m,n).则mn=k.
∵C是AB的中点,
∴C的坐标是(,).
∵C在反比例函数上,
∴•=k,即(m+a)n=4k,mn+an=4k.
∵△OAB的面积是6,
∴an=6,即an=12,
∴k+12=4k,
解得k=4.
故选:B.
【点评】本题考查了求反比例函数的解析式,正确设出未知数,转化为k的关系是关键.
26.(2022•钟楼区校级模拟)如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是( )
A.﹣2k1 B.2k2 C.k1+k2 D.k2﹣k1
【分析】先过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,再根据反比例函数系数k的几何意义,求得△ABE的面积=△COD的面积相等=|k2|,△AOE的面积=△CBD的面积相等=|k1|,最后计算平行四边形OABC的面积.
【解答】解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
根据∠AEB=∠CD0=90°,∠ABE=∠COD,AB=CO可得:△ABE≌△COD(AAS),
∴△ABE与△COD的面积相等,
又∵点C在y=的图象上,
∴△ABE的面积=△COD的面积相等=|k2|,
同理可得:△AOE的面积=△CBD的面积相等=|k1|,
∴平行四边形OABC的面积=2(|k2|+|k1|)=|k2|+|k1|=k2﹣k1,
故选:D.
【点评】本题主要考查了反比例函数系数k的几何意义,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.
27.(2022春•锡山区期末)点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,S2+S3=20,则S1的值为 10 .
【分析】根据CD=DE=OE以及反比例函数系数k的几何意义得到S1=k,S四边形OGQD=k,列方程即可得到结论.
【解答】解:∵CD=DE=OE,
∴S1=k,S四边形OGQD=k,
∴S2=(k﹣k×2)=,
S3=k﹣k﹣k=k,
∴k+k=20,
∴k=30,
∴S1=k=10,
故答案为:10.
【点评】本题考查反比例函数系数k的几何意义,矩形的性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
28.(2022春•惠山区期末)如图,四边形OACB是平行四边形,OB在x轴上,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,△AOF的面积为6,则k的值为 8 .
【分析】过F作FM⊥x轴于M,过C作CH⊥x轴于H,得到OD=BH,AD=CH,根据三角形的中位线的性质得到MF=HC=AD,设MF=a,则AD=2a,得到OD=,BM=OD=,根据OM•MF=k,得到k=8.
【解答】解:过F作FM⊥x轴于M,过C作CH⊥x轴于H,
则△ADO≌△CBH,
∴OD=BH,AD=CH,
∵点F为BC的中点,
∴MF=HC=AD,
设MF=a,则AD=2a,
∴OD=,
∴BM=OD=,
∵F在反比例函数的图象上,
∴OM•MF=k,
∴OM=,
∴DB=,
∴S△AOF=S梯形ADMF,
∴(a+2a)••=6,
∴k=8,
故答案为:8.
【点评】本题考查了反比例函数的系数k的几何意义,平行四边形的性质,作出辅助线构建全等三角形是解题的关键.
29.(2022•胶州市二模)如图,两个反比例函数y=和y=在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,若四边形PAOB的面积为5,则k= 8 .
【分析】根据反比例函数系数k的几何意义得到S矩形PCOD=k,S△AOC=S△BOD=,然后利用四边形PAOB的面积=S矩形PCOD﹣S△AOC﹣S△BOD进行计算.
【解答】解:∵PC⊥x轴,PD⊥y轴,∴S矩形PCOD=k,S△AOC=S△BOD==,
∴四边形PAOB的面积=S矩形PCOD﹣S△AOC﹣S△BOD=k﹣﹣=5.解得k=8.故答案是:8.
【点评】主要考查了反比例函数y=中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.
核心知识3.反比例函数与一次函数
30.(2022•攀枝花)如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x≤时,x的取值范围是( )
A.﹣1≤x<0或x≥1 B.x≤﹣1或0<x≤1
C.x≤﹣1或x≥1 D.﹣1≤x<0或0<x≤1
【分析】根据反比例函数的对称性求得B点的坐标,然后根据图象即可求得.
【解答】解:∵正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,
∴B(﹣1,﹣m),
由图象可知,当k1x≤时,x的取值范围是﹣1≤x<0或x≥1,
故选:A.
【点评】本题考查了反比例函数与一次函数的交点问题,利用函数的对称性求得B点的坐标,以及数形结合思想的运用是解题的关键.
31.(2022•宝安区校级模拟)如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m为常数且m≠0)的图象都经过A(﹣1,2),B(2,﹣1),结合图象,则不等式kx>﹣b的解集是( )
A.x<﹣1 B.﹣1<x<0
C.x<﹣1或0<x<2 D.﹣1<x<0或x>2
【分析】根据一次函数图象在反比例函数图象上方的x的取值范围便是不等式kx>﹣b的解集.
【解答】解:由函数图象可知,当一次函数y1=kx+b(k≠0)的图象在反比例函数y2=(m为常数且m≠0)的图象上方时,x的取值范围是:x<﹣1或0<x<2,
∴不等式kx>﹣b的解集是x<﹣1或0<x<2,
故选:C.
【点评】本题是一次函数图象与反比例函数图象的交点问题:主要考查了由函数图象求不等式的解集.利用数形结合是解题的关键.
32.(2022•普陀区校级开学)如图,一次函数y1=kx+b的图象与反比例函数的图象相交于点A(,4)和点B(3,n).若y1<y2,则x的取值范围是( )
A.x<0或<x<3 B.x<或x>3
C.0<x<或x>3 D.x<0或x>3
【分析】根据一次函数与反比例函数交点坐标,结合图象确定出所求x的范围即可.
【解答】解:根据图象得:当y1<y2时,x的取值范围是0<x<或x>3,
故选:C.
【点评】此题考查了反比例函数与一次函数的交点问题,利用了数形结合的思想,弄清数形结合思想是解本题的关键.
33.(2022春•德化县期中)如图,在平面直角坐标系中,直线y=mx(m≠0,m为常数)与双曲线(k≠0,k为常数)交于点A,B,若A(﹣1,a),B(b,﹣3),过点A作AM⊥x轴,垂足为M,连接BM,则△ABM的面积是( )
A.2 B.m﹣1 C.3 D.6
【分析】根据反比例的图象关于原点中心对称得到点A与点B关于原点中心对称,则S△OAM=S△OBM,A(﹣1,3),(1,﹣3),代入解析式求得k=﹣3,然后根据反比例函数y=(k≠0)系数k的几何意义即可得到S△AOM=|k|=,进一步得出S△ABM=2S△AOM=3.
【解答】解:∵直线y=mx(m≠0,m为常数)与双曲线(k≠0,k为常数)交于点A,B,
∴点A与点B关于原点中心对称,
∴S△OAM=S△OBM,
∵A(﹣1,a),B(b,﹣3),
∴a=3,b=1,
∴A(﹣1,3),(1,﹣3),
∴k=﹣1×3=﹣3,
∵AM⊥x轴,垂足为M,
∴S△AOM=|k|=,
∵S△OAM=S△OBM,
∴S△ABM=2S△AOM=3,
故选:C.
【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
34.(2021秋•东港区校级月考)如图,一次函数y=2x与反比例函数y=的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为,则k的值为( )
A. B. C. D.
【分析】作辅助线,先确定OQ长的最小时点P的位置,当BP延长线过圆心C时,BP最短,设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,根据勾股定理计算t的值,可得k的值.
【解答】解:连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=BP,
∵OQ长的最小值为,
∴BP长的最小值为×2=1,
如图,当BP的延长线过圆心C时,BP最短,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴22=(t+2)2+(﹣2t)2,
解得t=0(舍)或﹣,
∴B(﹣,﹣),
∵点B在反比例函数y=(k>0)的图象上,
∴k=﹣×(﹣)=;
故选:C.
【点评】本题考查了反比例函数与一次函数的交点问题、圆的性质,勾股定理的应用,有难度,解题的关键:利用勾股定理建立方程解决问题.
35.(2022•渠县一模)如图,直线y=ax+b与函数y=(x>0)的图象交于A(1,m)、B(n,1)两点,与x轴交于点C,且,则不等式ax+b>的解集在数轴上表示正确的是( )
A. B.
C. D.
【分析】作AD⊥x轴于D,BE⊥x轴于E,则AD∥BE,根据平行线分线段成比例定理求得m=3,即可求得A(1,3),根据反比例函数系数k=xy得到k=1×3=n•1,求得n=3,即B(3,1),观察图象即可得到不等式ax+b>的解集.
【解答】解:作AD⊥x轴于D,BE⊥x轴于E,则AD∥BE,
∴==,
∵A(1,m)、B(n,1),
∴AD=m,BE=1,
∴m=3,
∴A(1,3),
∵函数y=(x>0)的图象国过点A(1,3)、B(n,1)两点,
∴k=1×3=n•1,
∴n=3,
∴B(3,1),
观察图象,不等式ax+b>的解集为1<x<3,
故选:D.
【点评】本题是反比例函数与一次函数的交点问题,考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,函数与不等式的关系,求得B点的坐标、数形结合是解题的关键.
36.(2022•江汉区校级模拟)若一次函数y=kx+b和反比例函数y=(m<0)的图象交于点A(﹣3,y1),B(1,y2),则不等式kx2+bx﹣m<0的解集是( )
A.x>1或x<﹣3 B.0<x<1或x<﹣3
C.﹣3<x<0或x>1 D.﹣3<x<0或0<x<1
【分析】分两种情况讨论,观察一次函数y=kx+b(k≠0)图象和反比例函数y=(m<0)的图象,即可求得x的取值范围.
【解答】解:∵m<0,
∴反比例函数y=(m<0)的图象在第二、四象限,如图,
当x>0时,
∵kx2+bx﹣m<0,
∴kx+b<,
由函数图象可知,当一次函数y=kx+b(k≠0)图象在反比例函数y=(m<0)的图象下方时,x的取值范围是:x>1,
当x<0时,
∵kx2+bx﹣m<0,
∴kx+b>,
由函数图象可知,当一次函数y=kx+b(k≠0)图象在反比例函数y=(m<0)的图象上方时,x的取值范围是:x<﹣3,
∴等式kx2+bx﹣m<0的解集是:x>1或x<﹣3,
故选:A.
【点评】本题是一次函数图象与反比例函数图象的交点问题:主要考查了由函数图象求不等式的解集.利用数形结合是解题的关键.
核心知识4.待定系数法反比例函数解析式
37.(2022秋•冷水滩区校级月考)反比例函数的图象过点A(2,﹣8).
(1)求这个函数的表达式;
(2)请判断点B(﹣4,4)是否是这个反比例函数的图象上,并说明理由.
【分析】(1)把点A(2,﹣8)直接代入反比例函数,求得函数解析式即可;
(2)把点B(﹣4,4)代入(1)中的函数解析式,判断即可.
【解答】解:(1)∵反比例函数的图象过点A(2,﹣8).
∴k=2×(﹣8)=﹣16,
所以反比例函数的解析式为y=﹣;
(2)把x=﹣4代入y=﹣得,y=4,
∴点B(﹣4,4)在这个反比例函数的图象上.
【点评】此题考查待定系数法求函数解析式,反比例函数图象上点的坐标体系,将点的坐标代入解析式,利用方程解决问题.
38.(2022秋•娄星区校级月考)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(﹣3,n),B(2,3).
(1)求反比例函数与一次函数的函数表达式;
(2)请结合图象直接写出不等式kx+b≥的解集;
(3)若点P为x轴上一点,△ABP的面积为10,直接写出点P的坐标.
【分析】(1)根据反比例函数y=的图象经过B(2,3),利用待定系数法即可求出反比例函数的解析式;进而求得A的坐标,根据A、B点坐标,进而利用待定系数法求出一次函数解析式;
(2)根据A、B的坐标,结合图象即可求得;
(3)根据三角形面积求出CP的长,根据C的坐标即可得出P的坐标.
【解答】解:(1)∵反比例函数y=的图象经过B(2,3),
∴m=2×3=6.
∴反比例函数的解析式为y=.
∵A(﹣3,n)在y=上,所以n=﹣2.
∴A的坐标是(﹣3,﹣2).
把A(﹣3,﹣2)、B(2,3)代入y=kx+b.得,
解得,
∴一次函数的解析式为y=x+1.
(2)由图象可知:不等式kx+b≥的解集是﹣3≤x<0或x≥2;
(3)把y=0代入y=x+1得:0=x+1,
∴x=﹣1,
∴C的坐标是(﹣1,0),
∵P为x轴上一点,且△ABP的面积为10,A(﹣3,﹣2),B(2,3),
∴CP×2+CP×3=10,
∴CP=4,
∴当P在负半轴上时,P的坐标是(﹣5,0);
当P在正半轴上时,P的坐标是(3,0),
即P的坐标是(﹣5,0)或(3,0).
【点评】本题考查了用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,三角形的面积的应用,主要考查学生的计算能力.
39.(2022•微山县二模)如图,正方形OABC在平面直角坐标系中,点B的坐标是(2,2),顶点A,C在坐标轴上,反比例函数在第一象限的图象分别交AB,AC于点E,F,连接OF,EC交于点M,△OFC的面积等于1.
(1)求反比例函数的解析式;
(2)求四边形OAEM的面积.
【分析】(1)利用反比例函数系数k的几何意义即可求得;
(2)求得E、F的坐标,即可求得直线OF为y=x,直线EC为y=﹣2x+4,两直线解析式联立成方程组,解方程求得M点的坐标,然后根据四边形OAEM的面积=S正方形OABC﹣S△BCE﹣S△OCM求得即可.
【解答】解:(1)∵正方形OABC在平面直角坐标系中,顶点A,C在坐标轴上,
∴BC⊥x轴,
∴S△OFC=k=1,
∴k=2,
∴反比例函数的解析式为y=;
(2)∵B(2,2),
∴E点的纵坐标为2,F的横坐标为2,
∴E(1,2),F(2,1),
∴直线OF为y=x,直线EC为y=﹣2x+4,
解得,
∴M(,),
∴四边形OAEM的面积=S正方形OABC﹣S△BCE﹣S△OCM=2×2﹣×1×2﹣=.
【点评】本题考查了反比例函数系数k的几何意义,正方形的性质,反比例函数图象上点的坐标特征,利用分割法求得四边形的面积是解题的关键.
40.(2022•咸丰县模拟)如图,平面直角坐标系xOy中,函数的图象上A、B两点的坐标分别为A(n,n+1),B(n﹣5,﹣2n).
(1)求反比例函数和直线AB的解析式;
(2)连接AO、BO,求△AOB的面积.
【分析】(1)根据反比例函数系数k=xy得出n(n+1)=(n﹣5)(﹣2n),即n2+n=﹣2n2+10n3n2﹣9n=0,解方程求得A、B的坐标,进而即可利用待定系数法求得函数的解析式;
(2)求得D的坐标,然后利用三角形面积公式即可求得.
【解答】解:(1)∵A、B两点在的图象上,而A(n,n+1),B(n﹣5,﹣2n),
∴n(n+1)=(n﹣5)(﹣2n),即n2+n=﹣2n2+10n3n2﹣9n=0,
解得n1=0,n2=3
∵的图象与坐标轴没有交点,
∴n1=0舍去,
∴n=3,
∴A(3,4),B(﹣2,﹣6),
∴k=3×4=12,
设直线AB的解析式为:y=ax+b,
则,
解得:
∴直线AB的解析式为:y=2x﹣2,反比例函数解析式为:;
(2)设直线AB交x轴于点D,则
当y=0时,2x﹣2=0,
∴x=1,
∴D(1,0),
∴
∴△AOB的面积为5.
【点评】本题考查了待定系数法求反比例函数的解析式,一次函数的解析式,一次函数图象上点的坐标特征,三角形的面积,求得A、B点的坐标是解题的关键.
41.(2021秋•霸州市期末)如图,直线l:y=﹣x+4与x轴、y轴分别交于点A,B,点P,Q均在l上,点P的横坐标为m,点Q的横坐标为m+1,反比例函数(k>0,x>0)的图象L经过点P.
(1)若m=1,
①求L的解析式;
②判断L是否经过点Q,并说明理由.
(2)若L经过点Q,求m的值.
【分析】(1)①把x=1代入y=﹣x+4得,y=3,求得P(1,3),代入(k>0,x>0)即可得到结论;
②把x=2代入y=﹣x+4得到Q(2,2),由于2×2=4≠3,于是得到结论;
(2)根据题意得方程即可得到结论.
【解答】解:(1)①把x=1代入y=﹣x+4得,y=3,
∴P(1,3),
∵反比例函数(k>0,x>0)的图象L经过点P,
∴k=1×3=3,
∴L的解析式为y=;
②L不经过点Q,
理由:∵m=1,
∴点Q的横坐标为2,
把x=2代入y=﹣x+4得,y=2,
∴Q(2,2),
∵2×2=4≠3,
∴L不经过点Q;
(2)∵点P,Q均在l上,点P的横坐标为m,点Q的横坐标为m+1,
∴Q(m+1,﹣m+3),P(m,﹣m+4)
∵L经过点Q,点P,
∴(m+1)(﹣m+3)=m(﹣m+4),
解得m=.
【点评】本题考查了待定系数法求反比例函数的解析式,一次函数的性质,反比例函数点的坐标特征,正确地求得反比例函数的解析式是解题的关键.
核心知识5.反比例函数的应用
42.(2022•南京模拟)在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(4,3)在其图象上,则当力达到10N时,物体在力的方向上移动的距离是( )
A.2.4m B.1.2m C.1m D.0.5m
【分析】利用点P的坐标求出F=,当F=10时,即F==10,求出s,即可求解.
【解答】解:设函数的表达式F=,
将点P的坐标代入上式得:3=,
解得k=12,
则反比例函数表达式为F=,
当F=10时,即F==10,
解得s=1.2,
故选:B.
【点评】本题考查反比例函数的应用,用待定系数法求反比例函数解析式是解题关键.
43.(2022•宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
【分析】由油箱中油的体积V与电路中总电阻R总是反比例关系,电流I与R总是反比例关系,可得V=I(为常数),即可得到答案.
【解答】解:由油箱中油的体积V与电路中总电阻R总是反比例关系,设V•R总=k(k为常数),
由电流I与R总是反比例关系,设I•R总=k'(k为常数),
∴=,
∴V=I(为常数),
∴I与V的函数关系是正比例函数,
故选:B.
【点评】本题考查反比例函数与正比例函数的应用,解题的关键是掌握反比例函数与正比例函数的概念.
44.(2022春•无锡期末)古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N和0.5m,小明最多能使出500N的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )
A.至多为1.6m B.至少为1.6m
C.至多为0.625m D.至少为0.625m
【分析】直接利用:阻力×阻力臂=动力×动力臂,进而得出F与l之间的函数表达式;把F=500N代入所求的函数解析式即可得到结论.
【解答】解:由题意可得:1600×0.5=Fl,
则F与l的函数表达式为:F=;
当动力F=500N时,
500=,
解得l=,
答:动力F=500N时,动力臂至少为1.6m,
故选:B.
【点评】此题主要考查了反比例函数的应用,正确得出F与l之间的关系是解题关键.
45.(2022•大同三模)如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法正确的是( )
A.当R<0.25时,I<880
B.I与R的函数关系式是I=(R>0)
C.当R>1000时,I>0.22
D.当880<R<1000时,I的取值范围是0.22<I<0.25
【分析】由待定系数法求出反比例函数的解析式,根据反比例函数的性质逐项分析即可得到结论.
【解答】解:设I与R的函数关系式是I=(R>0),
∵该图象经过点P(880,0.25),
∴=0.25,
∴U=220,
∴I与R的函数关系式是I=(R>0),故选项B不符合题意;
当R=0.25时,I=880,当R=1000时,I=0.22,
∵反比例函数I=(R>0)I随R的增大而减小,
当R<0.25时,I>880,当R>1000时,I<0.22,故选项A,C不符合题意;
∵R=0.25时,I=880,当R=1000时,I=0.22,
∴当880<R<1000时,I的取值范围是0.22<I<0.25,故D符合题意;
故选:D.
【点评】本题主要考查了反比例函数的应用,由待定系数法求出反比例函数的解析式是解决问题的关键.
46.(2022秋•东平县校级月考)当下教育主管部门提倡加强高效课堂建设,要求教师课堂上要精讲,把时间、思考、课堂还给学生.通过实验发现:学生在课堂上听课注意力指标随上课时间的变化而变化,上课开始后,学生的学习兴趣递增,中间一段时间,学生的兴趣保持平稳高效状态,后阶段注意力开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段,当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值.
(2)如果学生在课堂上的注意力指标不低于30属于学习高效阶段,请你求出学生在课堂上的学习高效时间段.
【分析】(1)设反比例函数的解析式为y=,由C(20,45)求出k,可得D坐标,从而求出A的指标值;
(2)求出AB解析式,得到y≥30时x≥4,由反比例函数y=可得y≥30时,x≤30,即可得到答案.
【解答】解:(1)设当20≤x≤45时,反比例函数的解析式为y=,
将C(20,45)代入得:45=,
解得k=900,
∴反比例函数的解析式为y=,
当x=45时,y==20,
∴D(45,20),
∴A(0,20),即A对应的指标值为20;
(2)设当0≤x<10时,AB的解析式为y=mx+n,将A(0,20)、B(10,45)代入得:
,
解得,
∴AB的解析式为y=x+20,
当y≥30时,x+20≥30,
解得x≥4,
由(1)得反比例函数的解析式为y=,
当y≥30时,≥30,
解得x≤30,
∴4≤x≤30时,注意力指标都不低于30.
【点评】本题考查函数图象的应用,涉及一次函数、反比例函数及不等式等知识,解题的关键是求出0≤x<10和20≤x≤45时的解析式.
47.(2022秋•荣成市校级月考)疫情防控期间,某校校医每天早上对全校办公室和教室进行药物喷洒消毒,完成一间办公室和一间教室的喷洒共需8min;完成两间办公室和三间教室的喷洒共需21min.消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示.进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,后勤人员依次对一班至十一班教室(共11间)进行药物喷洒消毒,当最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.
【分析】设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,根据题意列方程组可得一间教室的药物喷洒时间为5min,即可根据点A在y=2x上,求出点A的坐标(5,10),从而得反比例函数表达式为y=,当x=55时,y=<1,即可作出判断.
【解答】解:设完成一间办公室和一间教室的药物喷洒各要xmin和ymin,
则,
解得,
∴一间教室的药物喷洒时间为5min,
∴11个教室需要55min,
当x=5时,y=2x=10,故点A(5,10),
设反比例函数表达式为:y=,将点A的坐标代入上式可解得:k=50,
∴反比例函数表达式为y=,
当x=55时,y=<1,
∴一班学生能安全进入教室.
【点评】本题主要考查反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
相关资料
更多









