数学选择性必修 第一册1.4 空间向量的应用完美版课件ppt

这是一份数学选择性必修 第一册1.4 空间向量的应用完美版课件ppt，共34页。PPT课件主要包含了常考题型，注意事项等内容，欢迎下载使用。

重点：理解直线的方向向量和平面的法向量，并会用直线的方向向量和平面的法向量证明直线与平面的位置关系.难点：建立立体图形与空间向量之间的联系，把立体几何问题转化为空间向量问题.
1.能用向量语言描述点、直线和平面，理解直线的方向向量和平面的法向量.2.能用向量语言描述直线与直线、直线与平面、平面与平面的垂直与平行关系.3.能用向量方法证明有关直线、平面位置关系的一些定理.
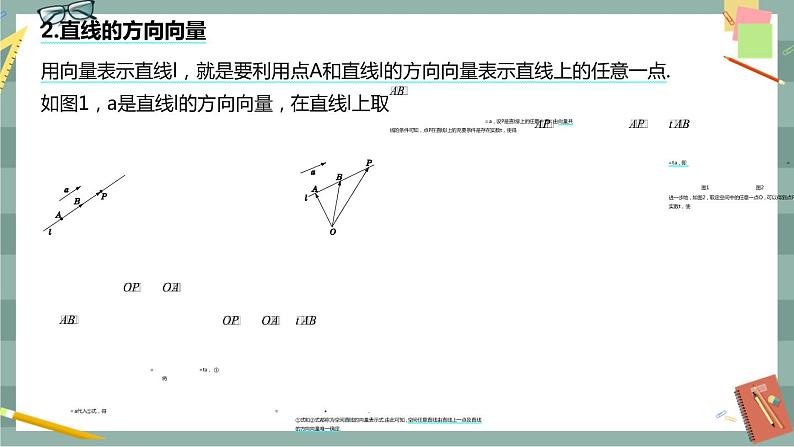
一、 空间中点、直线、平面的向量表示
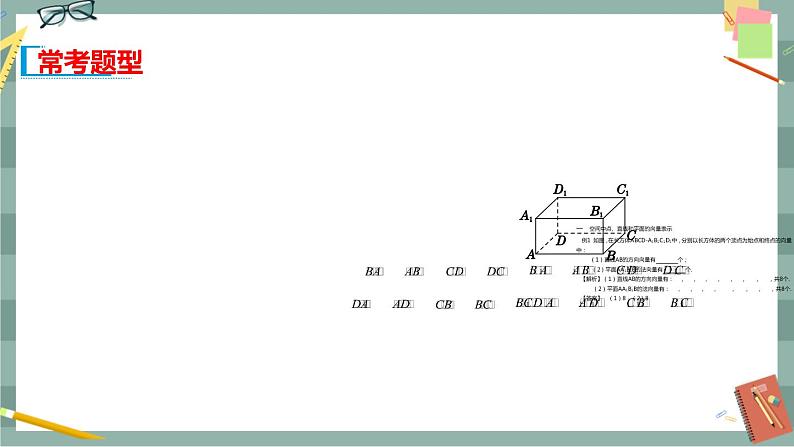
二、 空间中直线、平面的平行
三、 空间中直线、平面的垂直
解题方法：利用向量法证明线面平行的三种思路1.设直线l的方向向量是a，平面α的法向量是u，则要证明l∥α，只需证明a⊥u，即a·u＝0.2.根据线面平行的判定定理“若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行”，要证明平面外的一条直线和这个平面平行，只需在平面内找一个向量与已知直线的方向向量是共线向量即可.3.根据共面向量定理可知，如果一个向量和两个不共线的向量是共面向量，那么这个向量与这两个不共线的向量确定的平面必定平行，因此要证明平面外的一条直线和这个平面平行，只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
解题方法：面面平行的证明方法1.由面面平行的判定定理，要证明面面平行，只要转化为证明相应的线面平行、线线平行即可.2.若能求出平面α，β的法向量u，v，则要证明α∥β，只需证明u∥v.值得注意的是，虽然空间向量的坐标运算比线性运算更为简单，但法向量的求解有时比较烦琐，有时在平面内找与直线平行的向量也不直观，因此求解时，需要灵活选择解题方法.
三 空间中直线、平面的垂直
解题方法：利用向量法证明线面垂直1.基向量法具体步骤如下：（1）设出基向量，用基向量表示出直线的方向向量；（2）找出平面内两条相交直线的方向向量并分别用基向量表示；（3）分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积；（4）由数量积为0及线面垂直的判定定理得线面垂直.
2.坐标法具体方法如下:方法1：（1）建立空间直角坐标系；（2）将直线的方向向量用坐标表示；（3）将平面内任意两条相交直线的方向向量用坐标表示；（4）分别计算直线的方向向量与平面内两条相交直线的方向向量的数量积；（5）由数量积为0及线面垂直的判定定理得线面垂直.方法2：（1）建立空间直角坐标系；（2）将直线的方向向量用坐标表示；（3）求平面的法向量；（4）说明平面的法向量与直线的方向向量平行.