高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用巩固练习
展开
空间向量解答题10题
一、解答题(本大题共10小题,共100.0分)
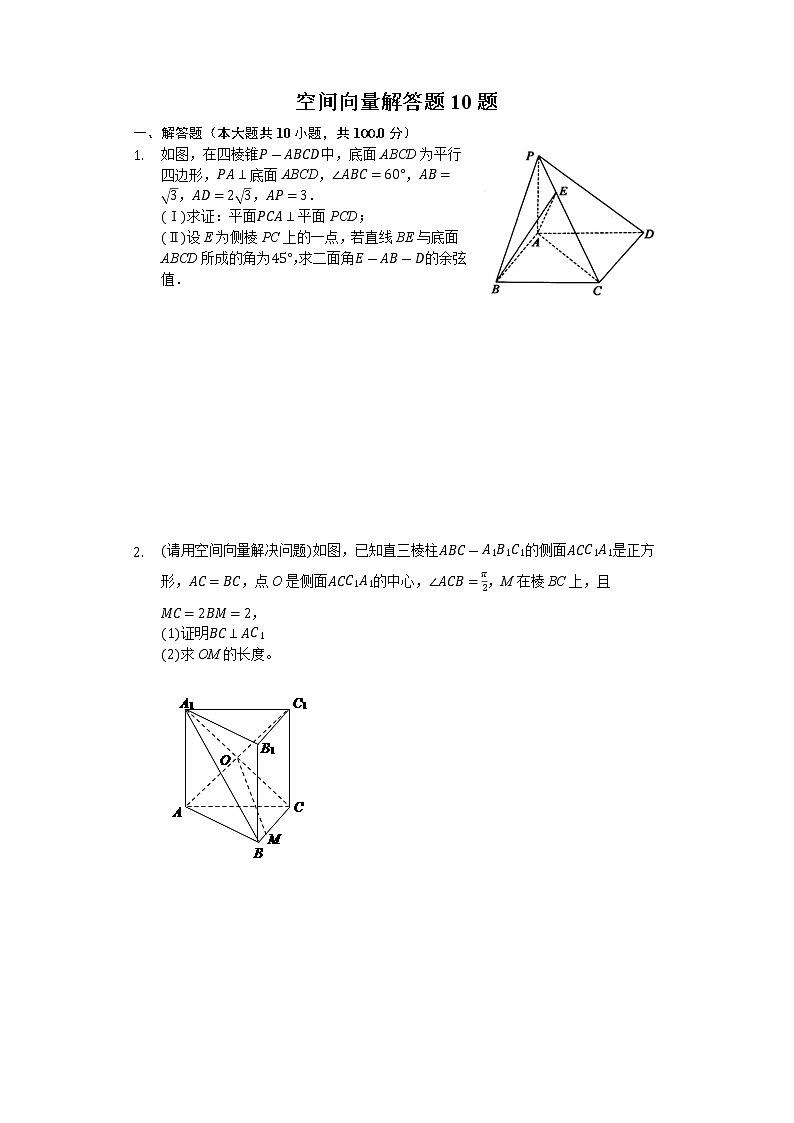
- 如图,在四棱锥中,底面ABCD为平行四边形,底面ABCD,,,,.
Ⅰ求证:平面平面PCD;
Ⅱ设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为,求二面角的余弦值.
|
- 请用空间向量解决问题如图,已知直三棱柱的侧面是正方形,,点O是侧面的中心,,M在棱BC上,且,
证明
求OM的长度。
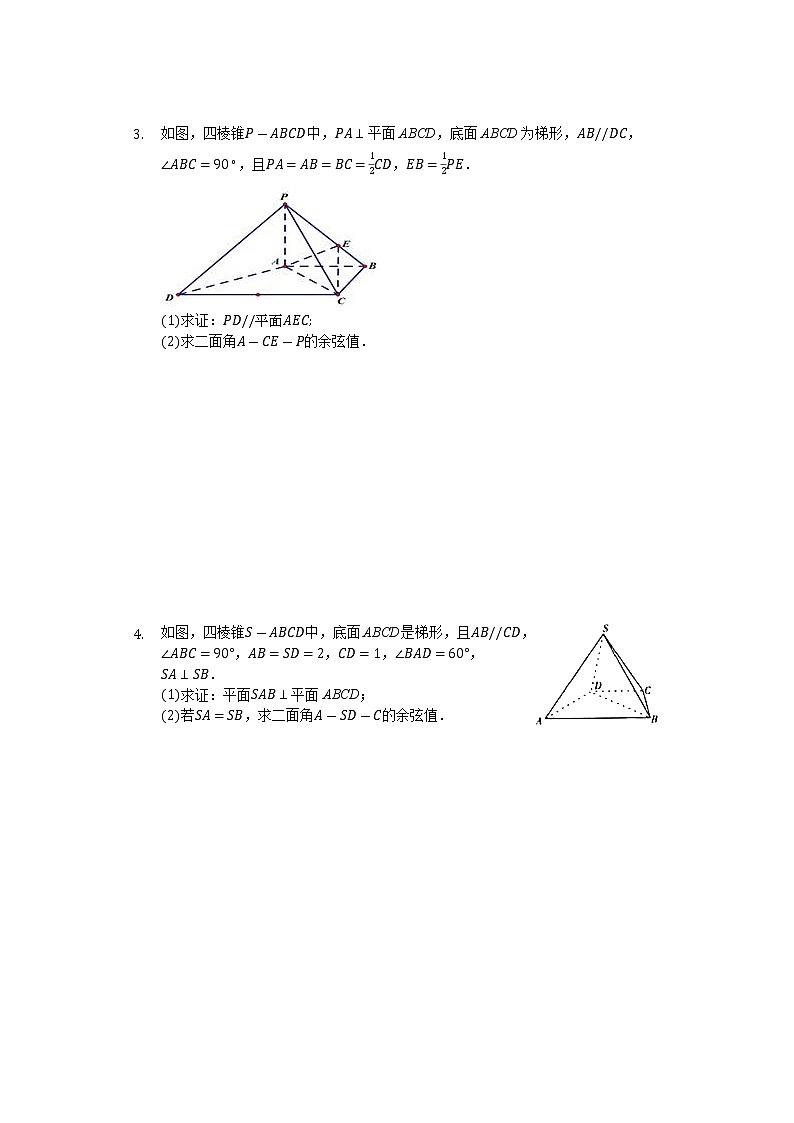
- 如图,四棱锥中,平面ABCD,底面ABCD为梯形,,,且,.
求证:
求二面角的余弦值.
- 如图,四棱锥中,底面ABCD是梯形,且,,,,,.
求证:平面平面ABCD;
若,求二面角的余弦值.
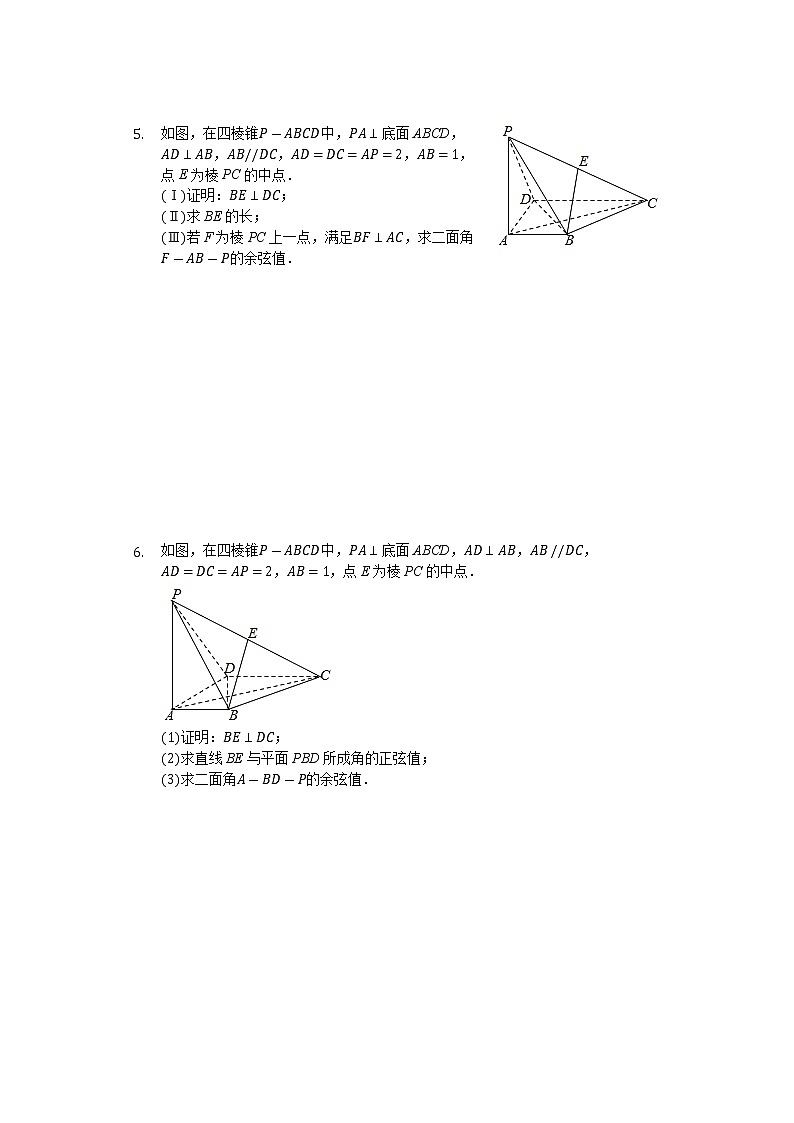
- 如图,在四棱锥中,底面ABCD,,,,,点E为棱PC的中点.
Ⅰ证明:;
Ⅱ求BE的长;
Ⅲ若F为棱PC上一点,满足,求二面角的余弦值.
|
- 如图,在四棱锥中,底面ABCD,,,,,点E为棱PC的中点.
证明:;
求直线BE与平面PBD所成角的正弦值;
求二面角的余弦值.
- 在四棱锥中,四边形ABCD为菱形,且,M,N分别为棱AP,CD的中点.
求证:平面PBC;
若平面ABCD,,求平面PBC与平面PAD所成二面角的正弦值.
|
- 如图,在四棱锥中,已知四边形ABCD是边长为的正方形,点S在底面ABCD上的射影为底面ABCD的中心点O,点P在棱SD上,且的面积为1.
若点P是SD的中点,求证:平面平面PAC;
在棱SD上是否存在一点P使得二面角的余弦值为?若存在,求出点P的位置;若不存在,说明理由.
- 如图,已知在直三棱柱中,,,,.
求的长度;
若,求二面角的余弦值.
- 如图,正方形ABCD的边长为4,,,把四边形ABCD沿AB折起,使得平面AEFB,G是EF的中点,如图.
图 图
求证:平面BCE;
求二面角的余弦值.
空间向量解答题10题
一、解答题(本大题共10小题,共100.0分)
- 如图,在四棱锥中,底面ABCD为平行四边形,底面ABCD,,,,.
Ⅰ求证:平面平面PCD;
Ⅱ设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为,求二面角的余弦值.
|
【答案】证明:Ⅰ在平行四边形ABCD中,,,,
由余弦定理得
,
,,,
底面ABCD,底面ABCD,,
又,AC、平面PCA,
平面PCA,
又平面PCD,平面平面PCD.
解:Ⅱ为侧棱PC上的一点,若直线BE与底面ABCD所成的角为,
如图,以A为坐标原点,AB,AC,AP分别为x,y,z轴,建立空间直角坐标系,
则0,,0,,3,,3,,0,,
设y,,,,则y,,3,,
,,
平面ABCD的一个法向量0,,
,
解得,
点E的坐标为1,,1,,,
设平面EAB的法向量y,,
则,取,得,
设二面角的平面角为,
则,
二面角的余弦值为.
【解析】本题考查面面垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
Ⅰ推导出,,从而平面PCA,由此能证明平面平面PCD;
Ⅱ以A为坐标原点,AB,AC,AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角的余弦值.
- 请用空间向量解决问题如图,已知直三棱柱的侧面是正方形,,点O是侧面的中心,,M在棱BC上,且,
证明
求OM的长度。
【答案】证明:以C为原点,CA为x轴,CB为y轴,为z轴,建立空间直角坐标系,
由题意得,,,,,,
,,
,
,则.
由得,,
,
.
【解析】本题考查利用向量法判断线线垂直及求长度,属中档题.
建立空间直角坐标系,利用数量积等于零判断垂直.
,.
- 如图,四棱锥中,平面ABCD,底面ABCD为梯形,,,且,.
求证:
求二面角的余弦值.
【答案】证明:连结BD,交AC于点M,连结EM,
,,
,
又,,
在中,.
不包含于平面EAC,平面EAC,
面EAC.
由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,
设,则0,,a,,a,,0,,
设y,为平面EAC的一个法向量,
则,
解得,,
同理可得平面PBC的一个法向量1,,
,,
二面角的余弦值为.
【解析】本题考查直线与平面平行的判断方法以及利用空间向量球二面角的基本方法.
由已知条件,推导出,利用直线与平面平行的判定定理能证明面EAC.
以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,求出平面EAC的一个法向量,平面PBC的一个法向量,利用向量的夹角公式,即可得出结论.
- 如图,四棱锥中,底面ABCD是梯形,且,,,,,.
求证:平面平面ABCD;
若,求二面角的余弦值.
【答案】解:取AB中点O,连接BD、DO、SO,
在直角梯形ABCD中,,,,,
,四边形BCDO为矩形,,
,.
,.
,面SAB,平面SAB.
平面ABCD,平面平面ABCD.
,.
由知,平面平面ABCD,平面ABCD,
直线OD,OB,OS两两垂直.以O为原点建立空间直角坐标系,如图,
则
.
.
设平面ASD的法向量为y,,
由,得,取,得,
设平面SCD的法向量为,由,得,取,
得,
,
由图可知二面角为钝二面角,
二面角的余弦值为.
【解析】本题考查面面垂直的判定,考查空间几何点线面的位置关系及向量法求解二面角的三角函数值,属中档常规题.
取AB中点O,连接BD、DO、SO,证明平面然后证明平面平面ABCD.
以O为原点建立空间直角坐标系,求出平面ASD的法向量,平面SCD的法向量,由图判断二面角为钝二面角,利用空间向量的数量积求解即可.
- 如图,在四棱锥中,底面ABCD,,,,,点E为棱PC的中点.
Ⅰ证明:;
Ⅱ求BE的长;
Ⅲ若F为棱PC上一点,满足,求二面角的余弦值.
|
【答案】Ⅰ证明:底面ABCD,,
以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立空间直角坐标系,
由题意0,,0,,2,,
1,,2,,
1,,0,,
,.
Ⅱ解:1,,
的长为.
Ⅲ解:,
2,,由点F在棱PC上,设,,
,
,,解得,
设平面FBA的法向量为,
则,
取,得,
取平面ABP的法向量1,,
则二面角的平面角满足:
,
二面角的余弦值为.
【解析】本题主要考查直线与平面、平面与平面之间的平行、垂直等位置关系,考查线线垂直、二面角的概念、求法等知识,考查空间想象能力和逻辑推理能力,是较难的题.
Ⅰ以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,求出
1,,0,,由,能证明.
Ⅱ由1,,能求出BE的长.
Ⅲ由,求出,进而求出平面FBA的法向量和平面ABP的法向量,由此利用向量法能求出二面角的余弦值.
- 如图,在四棱锥中,底面ABCD,,,,,点E为棱PC的中点.
证明:;
求直线BE与平面PBD所成角的正弦值;
求二面角的余弦值.
【答案】证明:如图,取PD中点M,连接EM,AM.
,M分别为PC,PD的中点,
,且,
又由已知,可得,且,
四边形ABEM为平行四边形,.
底面ABCD,,,
平面PAD,
,
.
解:连接BM,由有平面PAD,得,
而,.
又,M为PD的中点,,
,平面BEM,
平面平面PBD.
直线BE在平面PBD内的射影为直线BM,
,为锐角,
为直线BE与平面PBD所成的角.
依题意,有,而M为PD中点,
,.
在直角三角形BEM中,,
直线BE与平面PBD所成角的正弦值为.
以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
0,,2,,0,,
2,,0,,
设平面BDP的法向量y,,
则,取,得1,,
平面ABD的法向量0,,
设二面角的平面角为,
则.
二面角的余弦值为.
【解析】本题考查线面平行的证明,考查线面角的正弦值的求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.
取PD中点M,连接EM,AM,推导出四边形ABEM为平行四边形,平面PAD,由此能证明.
连接BM,推导出,,从而直线BE在平面PBD内的射影为直线BM,为直线BE与平面PBD所成的角,由此能求出直线BE与平面PDB所成角的正弦值.
以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角的余弦值.
- 在四棱锥中,四边形ABCD为菱形,且,M,N分别为棱AP,CD的中点.
求证:平面PBC;
若平面ABCD,,求平面PBC与平面PAD所成二面角的正弦值.
|
【答案】证明:设PB的中点为G,连接MG,GC,
,G分别为AP,PB的中点,,且,
由已知得,且,
,且.
四边形MGCN是平行四边形,
.
平面PBC,平面PBC,
平面PBC;
解:连接AC,BD,设,连接CO,OG,
设菱形ABCD的边长为a,由题设得,,,,
平面ABCD,分别以OA,OB,OG为x轴,y轴,z轴的非负半轴,
建立如图所示的空间直角坐标系,
则,0,,,,0,,
,,
设是平面PBC的一个法向量,
则,令,得.
同理可求得平面PAD的一个法向量为.
.
则平面PBC与平面PAD所成二面角的正弦值为.
【解析】设PB的中点为G,连接MG,GC,由三角形中位线定理可得,且,结合已知得到,且,则四边形MGCN是平行四边形,求得,再由线面平行的判定可得平面PBC;
连接AC,BD,设,连接CO,OG,设菱形ABCD的边长为a,由题设得,,,,平面ABCD,分别以OA,OB,OG为x轴,y轴,z轴的非负半轴建立空间直角坐标系,分别求出平面PBC与平面PAD的一个法向量,由两法向量所成角的余弦值可得平面PBC与平面PAD所成二面角的正弦值.
本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用空间向量求解空间角,是中档题.
- 如图,在四棱锥中,已知四边形ABCD是边长为的正方形,点S在底面ABCD上的射影为底面ABCD的中心点O,点P在棱SD上,且的面积为1.
若点P是SD的中点,求证:平面平面PAC;
在棱SD上是否存在一点P使得二面角的余弦值为?若存在,求出点P的位置;若不存在,说明理由.
【答案】解:因为点S在底面ABCD上的射影为O,所以平面ABCD,
因为四边形ABCD是边长为的正方形,所以,
又因为的面积为1,所以,
所以,因为,点P为SD的中点,
所以,同理可得,
因为,平面PAC,
所以平面PAC,
又,
平面平面PAC.
连接OB,易得OB,OC,OS两两垂直,
分别以OB,OC,OS所在直线为x,y,z轴建立空间直角坐标系,
则,1,,0,,0,,
假设存在P使二面角的余弦值为,
设,,
,所以,,
设平面PAC的一个法向量为,则
因为,
所以,令,得,,
因为平面ACD的一个法向量为,
所以
,
化简得,解得或舍,
所以存在P点符合题意,点P为棱SD靠近S的三等分点.
【解析】本题考查面面垂直的判定及二面角的求法,属于中档题.
求得,即可证出,同理可得,从而证得平面PAC,即可证得平面平面
连接OB,易得OB,OC,OS两两垂直,分别以OB,OC,OS所在直线为x,y,z轴建立空间直角坐标系,设,,先求得P的坐标,再求出面PAC的一个法向量即可求解.
- 如图,已知在直三棱柱中,,,,.
求的长度;
若,求二面角的余弦值.
【答案】解: 分别以AB,AC,所在直线为x轴,y轴,z轴,建立空间直角坐标系.
设,则0,,4,,0,,4,,所以4,,4,.
因为,所以,即,解得负值舍去,所以.
因为,所以0,.
又4,,0,,
所以4,,0,.
设y,为平面的一个法向量,则即取,解得,
所以1,为平面的一个法向量.
显然0,为平面的一个法向量,
则,,
所以二面角的余弦值为.
【解析】本题主要考查利用空间向量求二面角的平面角的求法,以及两点间距离的求解,考查了学生的计算能力.
分别以AB,AC,所在直线为x轴,y轴,z轴,建立空间直角坐标系设,利用向量的垂直即可求出t的值;
根据点的坐标,求出平面的法向量,因为0,为平面的一个法向量,利用空间向量的数量积求解二面角的余弦值即可.
- 如图,正方形ABCD的边长为4,,,把四边形ABCD沿AB折起,使得平面AEFB,G是EF的中点,如图.
图 图
求证:平面BCE;
求二面角的余弦值.
【答案】解:证明:连接BG,
因为,底面AEFB,
所以底面AEFB,
又底面AEFB,
所以,
因为,,
所以四边形ABGE为菱形,
所以,
又,平面BCE,平面BCE,
所以平面BCE;
由知四边形ABGE为菱形,,,
设,所以,,
以O为坐标原点,建立如图所示的空间直角坐标系,
则0,,0,,,,,
0,,
所以,,
设平面ACE的法向量为y,,则,
所以
令,则,,
即平面ACE的一个法向量为1,,
易知平面AEF的一个法向量为0,,
设二面角的大小为,
由图易知,
所以 .
【解析】本题考查了线面垂直的判断,空间直角坐标系,空间向量夹角的求解问题.
由条件得到,以及通过ABGE为菱形,得到,证得结论;
由知四边形ABGE为菱形,,,以O为坐标原点,建立如图所示的空间直角坐标系,则0,,0,,,,,0,,设平面ACE的法向量为y,,求出后,易得平面AEF的一个法向量为0,,设二面角的大小为,由图易知,所以,这样就能求出二面角的余弦值.
人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示课后练习题: 这是一份人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示课后练习题,共9页。
选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用练习题: 这是一份选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用练习题,共14页。试卷主要包含了选择题,解答题,填空题等内容,欢迎下载使用。
人教A版 (2019)选择性必修 第一册1.4 空间向量的应用同步达标检测题: 这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用同步达标检测题,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













