初中数学北师大版八年级上册第五章 二元一次方程组6 二元一次方程与一次函数一课一练

6　二元一次方程与一次函数

核心回顾

1．任何二元一次方程都可以化成__一次函数__的形式．

2．二元一次方程有__无数__个解，它的解与一次函数图象上的点的__坐标__是一一对应的．

3．含两个二元一次方程的方程组都对应两个一次函数，两个一次函数的__交点坐标__就是相应的二元一次方程组的解．

4．当两个一次函数的图象相交时，方程组有唯一的__一组__解；当两个一次函数的图象__平行__时，方程组无解；当两个一次函数的图象重合时，方程组有__无数__组解．

微点拨

二元一次方程与一次函数的关系

1．形式可互化：任何一个二元一次方程都可化为一次函数的表达式的形式，反过来也可以．

2．二元一次方程的解有无数个，以这个二元一次方程的所有的解为坐标的点组成的图象与这个二元一次方程转化的一次函数的图象相同．

3．二元一次方程与一次函数之间的对应关系体现了“数形结合”的思想．

基础必会

1．以方程－2x－y＝14的解为坐标的点组成的图象是一条直线，这条直线对应的一次函数表达式为(C)

A．y＝－2x＋14      B．y＝2x－14   

C．y＝－2x－14      D．y＝－x＋7

2．若关于x，y的二元一次方程组的解为，一次函数y＝kx＋b与y＝mx＋n的图象的交点坐标为(A)

A．(1，2)    B．(2，1)

C．(2，3)    D．(1，3)

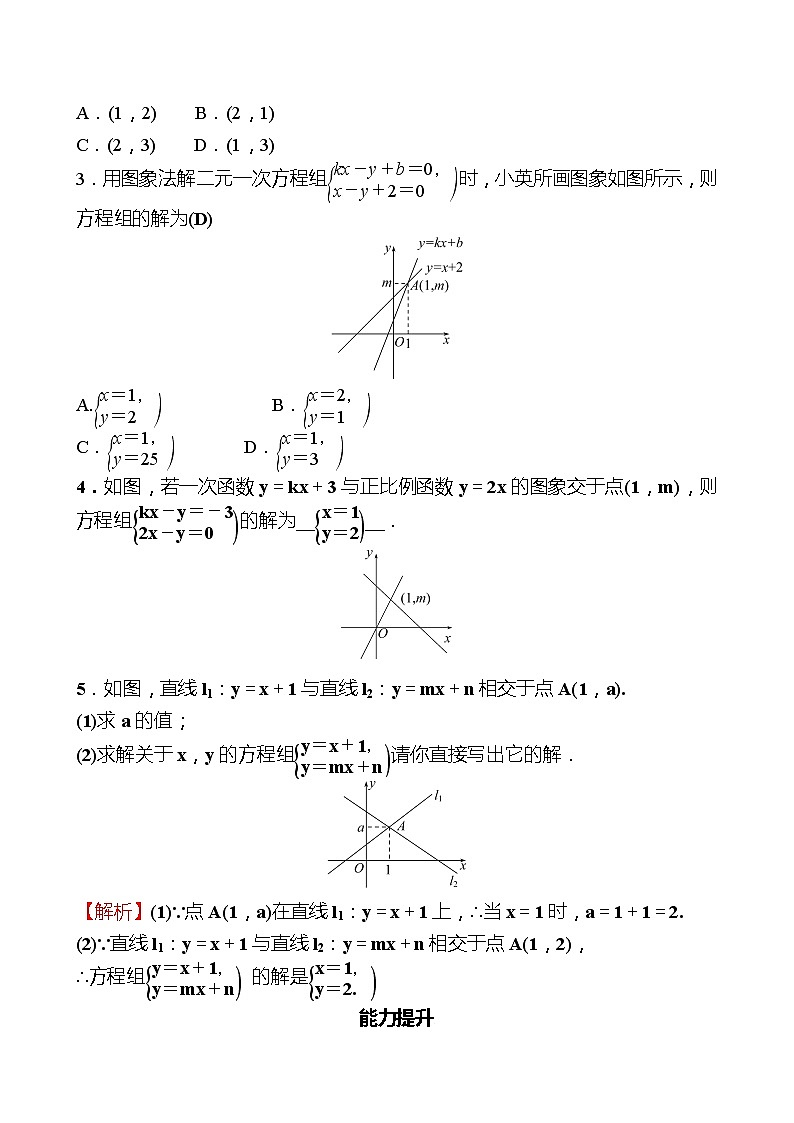
3．用图象法解二元一次方程组时，小英所画图象如图所示，则方程组的解为(D)

A.       B．   

C．      D．

4．如图，若一次函数y＝kx＋3与正比例函数y＝2x的图象交于点(1，m)，则方程组的解为____．

5．如图，直线l1：y＝x＋1与直线l2：y＝mx＋n相交于点A(1，a).

(1)求a的值；

(2)求解关于x，y的方程组请你直接写出它的解．

【解析】(1)∵点A(1，a)在直线l1：y＝x＋1上，∴当x＝1时，a＝1＋1＝2.

(2)∵直线l1：y＝x＋1与直线l2：y＝mx＋n相交于点A(1，2)，

∴方程组 的解是

能力提升

1．以二元一次方程2x－y＝1的解为坐标的点组成的图象画在坐标系中可能是(B)

2．在同一直角坐标系内分别作出一次函数y＝x＋1和y＝2x－2的图象，则下面的说法：

(1)函数y＝2x－2的图象与y轴的交点是(－2，0)；

(2)方程组的解是

(3)函数y＝x＋1和y＝2x－2的图象交点的坐标为(－2，2)；

(4)两直线与x轴所围成的三角形的面积为3.

其中正确的有__(2)(4)__(填序号).

3.如图，直线l1：y＝kx＋b与直线l2：y＝－x＋4交于点C，直线l1经过点.

(1)求直线l1的函数表达式；

(2)直接写出方程组的解为______；

(3)若点P在直线l1的下方，直线l2的上方，写出n的取值范围为______．

【解析】(1)当y＝2时，－x＋4＝2，解得x＝2，即C点坐标为；由y＝kx＋b与直线l2：y＝－x＋4交于点C，直线l1经过点，得，解得，

直线l1的函数表达式为y＝2x－2；

(2)方程组的解即为交点C横纵坐标的值，C点坐标为，所以方程组的解为；

答案：

(3)由题意可知当x＝3，y1>n>y2，y1＝2x－2＝2×3－2＝4，y2＝－x＋4＝－3＋4＝1.

所以1<n<4.

答案：1<n<4