高中数学北师大版 (2019)必修 第二册5.2 平面与平面垂直一课一练

这是一份高中数学北师大版 (2019)必修 第二册5.2 平面与平面垂直一课一练，共18页。试卷主要包含了点S，如图所示为一个正方体的展开图，如图所示，在正方体中，等内容，欢迎下载使用。

1．如图所示为水平放置的正方形，在平面直角坐标系中点的坐标为，用斜二测画法画出它的直观图，则点到轴的距离为_____________.
2．若正三棱柱的棱长均相等，则与侧面所成角的正切值为___.
3．点S．A．B．C在半径为的同一球面上，点S到平面ABC的距离为，，则点S与中心的距离为________．
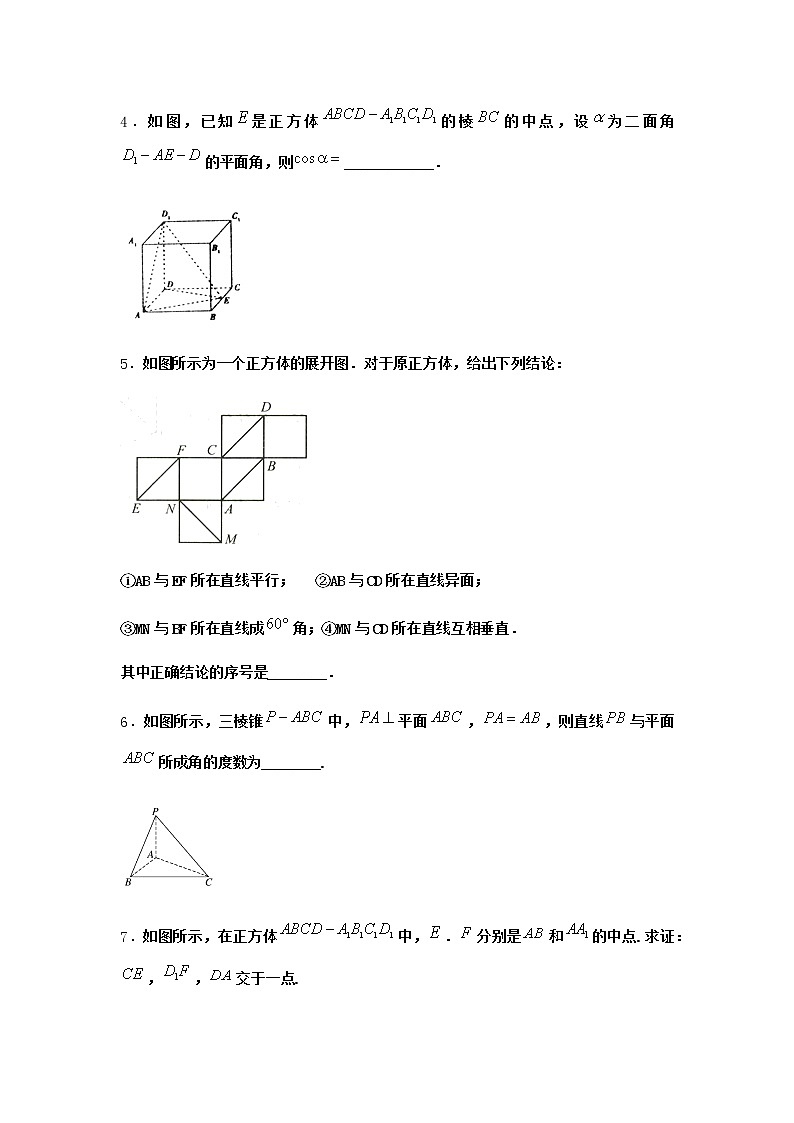
4．如图，已知是正方体的棱的中点，设为二面角的平面角，则____________．
5．如图所示为一个正方体的展开图．对于原正方体，给出下列结论：
①AB与EF所在直线平行； ②AB与CD所在直线异面；
③MN与BF所在直线成角；④MN与CD所在直线互相垂直．
其中正确结论的序号是________．
6．如图所示，三棱锥中，平面，，则直线与平面所成角的度数为________.
7．如图所示，在正方体中，．分别是和的中点.求证：，，交于一点.
8．如图,AB为圆O的直径,点C在圆周上异于点A,,直线PA垂直于圆O所在的平面,点M是线段PB的中点有以下四个命题：
①∥平面；
②∥平面；
③平面；
④平面平面．
其中正确的命题的序号是______．
9．已知二面角为60，，，A为垂足，，，，则异面直线与所成角的余弦值为______________.
10．在四面体ABCD中，AB=AD=2，∠BAD=60°，∠BCD=90°，二面角A-BD-C的大小为120°，则四面体ABCD外接球的半径为______
11．设三棱锥的底面是正三角形，侧棱长均相等，是棱上的点（不含端点），记直线与直线所成的角为，直线与平面所成的角为，二面角的平面角为，则三个角．．中最小的角是______.
12．在正四面体中，分别是的中点，下面四个结论：
①//平面
②平面
③平面平面
④平面平面
其中正确结论的序号是______________.
13．已知三棱锥满足平面平面，，，，则该三棱锥的外接球的表面积为________________.
14．在正方体中，二面角的大小为__________.
15．体积为的三棱锥的顶点都在球的球面上，平面，，， 则球的表面积的最小值为________.
参考答案与试题解析
1．【答案】.
【解析】根据斜二测画出，画出直观图，计算，求解即可.
【详解】
在直观图中，，，故点到轴的距离为.
故答案为：
【点睛】
本题考查斜二测画法，属于较易题.
2．【答案】
【解析】设棱长为1.取中点,连接,根据正三棱柱的特点,,根据线面角的定义可知,为与侧面所成角,在中，.
考点：线面角的定义.
3．【答案】
【解析】设的外接圆的圆心为.连接 过作于点.由题意可求出，从而得到，即可得到，在中即可求出点S与中心的距离 .
【详解】
如图所示：
设的外接圆的圆心为.连接 过作于点.
因为.
所以的外接圆半径.
所以.
因为点S到平面ABC的距离为,平面,
所以 .即
在中： .
所以 .
故填：.
【点睛】
本题考查球上的点到三角形中心的距离的求法,属于中档题,解题时要认真审题，注意球的性质和空间思维能力的培养.
4．【答案】
【解析】首先过点作，连接，可证明是二面角的平面角，然后求解.
【详解】
如图，过点作，连接
，
平面，
是二面角的平面角，
设棱长为2，则正方形的面积是4，
是的中点，
，
，
，
， ,
.
故答案为：
【点睛】
本题考查二面角的平面角的求法，意在考查空间想象和计算能力，属于基础题型.
5．【答案】②④
【解析】先将展开图还原为正方体，再由图观察即可得解.
【详解】
由展开图可知，各点在正方体中的位置如图：
由图可知，，①不正确；,异面，②正确；
,③不正确；，④正确，
故答案为：②④.
【点睛】
本题考查了两直线平行．垂直的判定，属中档题.
6．【答案】
【解析】因为平面，所以即为所求.
【详解】
由已知平面，所以即为直线与平面所成角，又，所以.
故答案为.
【点睛】
本题主要考查直线与平面所成角的问题，属基础题.
7．【答案】试题分析：根据两个面的公共点一定在两个面的公共线上，只需证出与交点在上即可.
【详解】
证明：如图所示，连接．．，
因为．分别是和的中点，
所以且.
即：，且，
所以四边形是梯形，
所以与必相交，设交点为，
则，且，又平面，
且平面，所以平面，
且平面，
又平面平面，所以，
所以．．三线交于一点.
【点睛】
本题主要考查线共点，考查了学生的逻辑推理能力，属于基础题.
【解析】
8．【答案】①④
【解析】根据线面平行的判定与线面,面面垂直的判定方法逐个证明即可.
【详解】
对①,因为为的中点,故为三角形的中位线,故∥平面.
故①正确.
对②,因为平面,故②错误.
对③,因为,故不会垂直于,故不垂直于平面.故③错误
对④, 因为,面,故.又.
故平面,又平面,故平面平面.故④正确.
故答案为①④
【点睛】
本题主要考查了线面平行与线面垂直等判定,属于中等题型.
9．【答案】
【解析】首先作出二面角的平面角,然后再构造出异面直线与所成的角,利用解直角三角形,可求出问题的答案.
【详解】
如图所示:
过作于,于,再过作的平行线与过作的垂线交于,连接,则为二面角的平面角,易知四边形为矩形.
由知,所以为与所成的角,
设,因为,则,又由条件知,且,
所以在△中,,
所以在△中,.
故答案为: .
【点睛】
本题主要考查异面直线所成角,二面角,直线与平面间的垂直关系,属于中档题.
10．【答案】
【解析】利用和的外心找出球心，然后计算．
【详解】
如图，取中点，则直角的外心，作平面，，连接，∵是等边三角形，∴，∴平面，从而平面平面，在上取点，设，则是正三角形的中心，在平面内作交于，则平面，是四面体外接球的球心．在平面内过，则是二面角的平面角，，于是，，，∴．
故答案为：．
【点睛】
本题考查四面体的外接球问题，解题关键是找到外接球的球心，注意性质：外接球球心一定在过各面的外心且与各面垂直的直线上．
11．【答案】
【解析】作出线线角，线面角，二面角，根据它们的正弦值，比较出它们的大小关系.
【详解】
作交于，由于，，所以为正三棱锥，由对称性知.取中点，连接，作平面，交平面于，连接.作平面，交平面于，连接.作，交于，连接，所以.由于，所以.由于平面，所以.由于，平面，所以.
.因为，在上，平面于，平面于，所以.所以.所以.由于都是锐角，所以.
由于在上，由对称性，而，则，由于也是锐角，所以.
综上所述，三个角中的最小角是.
故答案为：.
【点睛】
本小题主要考查线线角．线面角．二面角的概念，考查数形结合的数学思想方法，考查空间想象能力，属于中档题.
12．【答案】①②④
【解析】如图所示,由已知条件利用线面平行,线面垂直,面面垂直的判定直接推导即可得出答案.
【详解】
如图所示,在正四面体P-ABC中,D,F分别是AB,CA的中点,则DF//BC,
因为平面PDF,BC？平面PDF,所以BC//平面PDF,故①正确;
由PB=PC,AB=AC,E为中点,得,所以平面PAE,由DF//BC得DF平面PAE,故②正确;
过P作PO平面ABC,垂足为O,由题意得O点为底面△ABC的中心,且点O在AE上,AO=AE,
设AE与DF的交点为M,则由AM=AE,故点O,M不重合,则平面PDF和平面ABC不垂直,故③不正确;
由②得平面PAE,BC？平面PBC,所以平面PBC平面PAE,故④正确,综上可得正确的序号为①②④.
故答案为:①②④.
【点睛】
本题考查了线面平行,线面垂直,面面垂直的判定,熟练掌握线面平行,线面垂直,面面垂直的判定定理是解题的关键,属于基础题.
13．【答案】
【解析】先确定球心就是的外心，再利用正弦定理得到，计算表面积得到答案.
【详解】
因为，所以的外心为斜边的中点，
因为平面平面，所以三棱锥的外接球球心在平面上，
即球心就是的外心，根据正弦定理，解得，
所以外接球的表面积为.
【点睛】
本题考查了三棱锥的外接球问题，确定球心为的外心是解题的关键.
14．【答案】
【解析】由线面垂直性质得，又，可得二面角平面角为，由得到结果.
【详解】
平面，平面
又，平面 即为二面角的平面角
二面角的大小为
故答案为：
【点睛】
本题考查立体几何中二面角的求解，关键是能够根据二面角平面角的定义找到二面角的平面角.
15．【答案】
【解析】设出三角形的三边长，利用三棱锥的体积列方程.计算出三角形的外接圆半径，由此计算出球的半径的表达式，并求得球的半径的最小值，进而求得其表面积的最小值.
【详解】
设三条边长为，则
①.
由于平面，所以三棱锥的体积为，所以②.
设的外心为，球的球心为.
由正弦定理得外接圆的半径为.
由图可知，球的半径，将①代入上式得
，当且仅当时等号成立.故球表面积的最小值为.
故答案为：.
【点睛】
本小题主要考查有关几何体外接球表面积的最小值的计算，考查三棱锥的体积公式，考查基本不等式求最值，考查正弦定理和余弦定理解三角形，考查空间想象能力，属于中档题.