数学九年级上册22.1.2 二次函数y＝ax2的图象和性质示范课ppt课件

这是一份数学九年级上册22.1.2 二次函数y＝ax2的图象和性质示范课ppt课件，共19页。PPT课件主要包含了二次函数，二次函数的图像，画函数yx2的图像，解1列表，2描点，3连线，yx2，y－x2，y-x2，例题与练习等内容，欢迎下载使用。

一般地,形如 y=ax2+bx+c(a、b、c为常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
下列哪些函数是二次函数？哪些是一次函数？(1) y=3x-l (2) y=2x²＋7 (4) y=x-2 (5) y=(x+3)²-x² (6) y=3(x-1)²+1
一次函数的图象是一条_____，
(2) 通常怎样画一个函数的图象？
(3) 二次函数的图象是什么形 状呢？
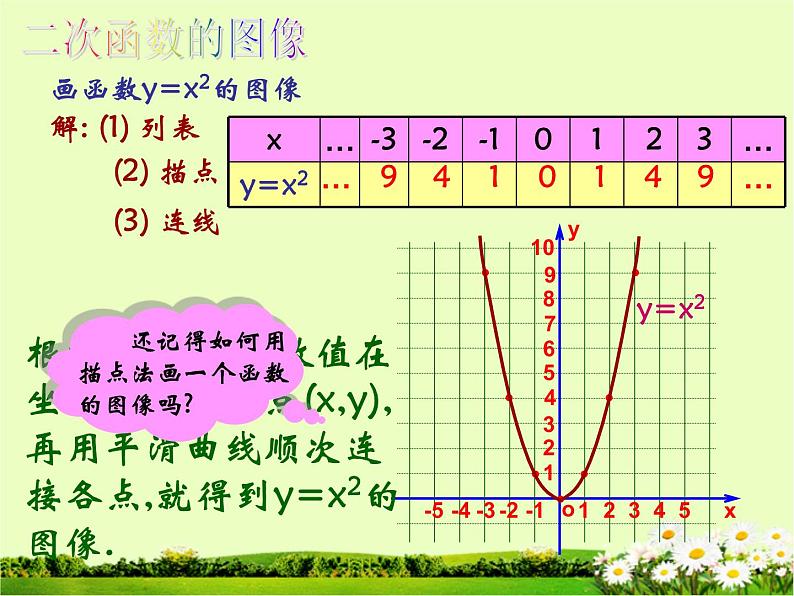
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
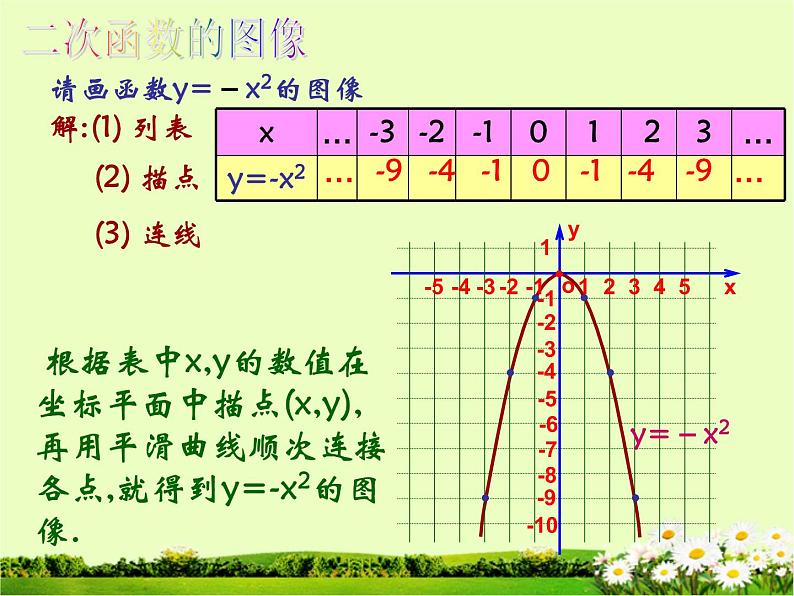
请画函数y=－x2的图像
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=-x2的图像.
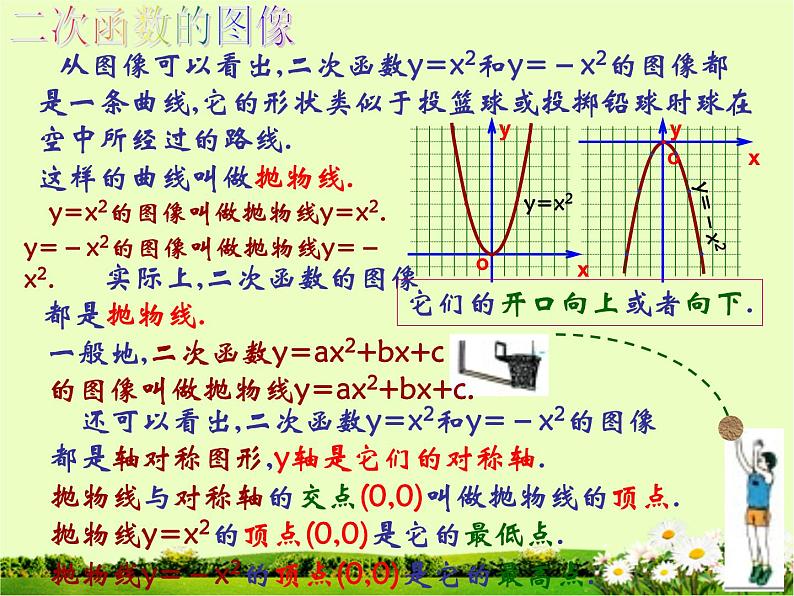
从图像可以看出,二次函数y=x2和y=－x2的图像都是一条曲线,它的形状类似于投篮球或投掷铅球时球在空中所经过的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
y=－x2的图像叫做抛物线y=－x2.
实际上,二次函数的图像都是抛物线.
它们的开口向上或者向下.
一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c.
还可以看出,二次函数y=x2和y=－x2的图像都是轴对称图形,y轴是它们的对称轴.
抛物线与对称轴的交点(0,0)叫做抛物线的顶点.
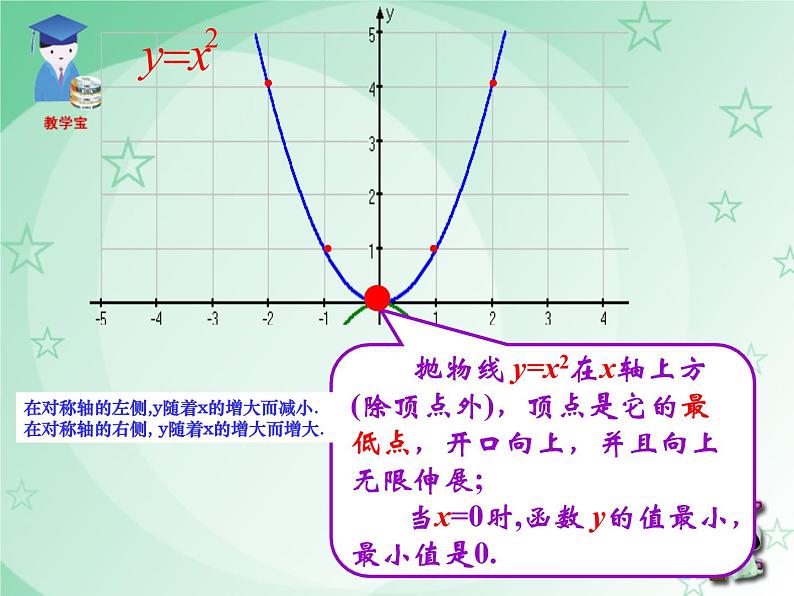
抛物线y=x2的顶点(0,0)是它的最低点.
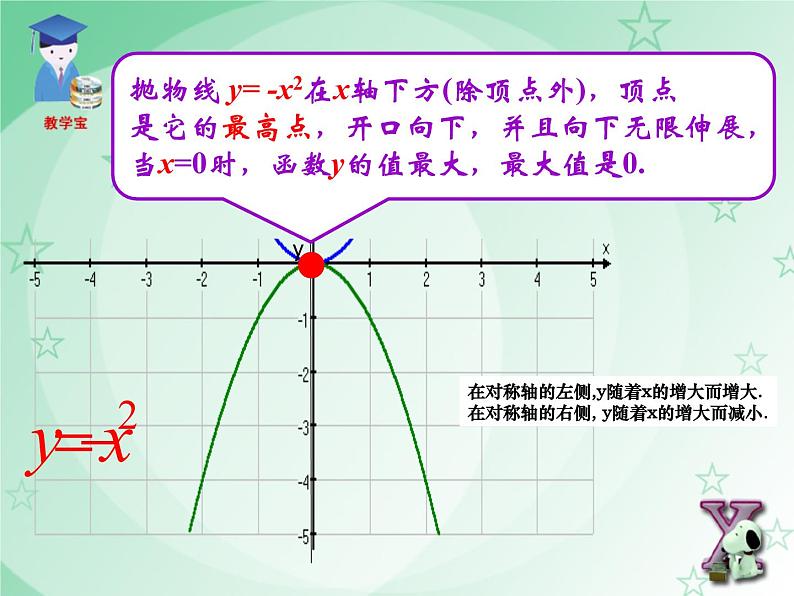
抛物线y=－x2的顶点(0,0)是它的最高点.
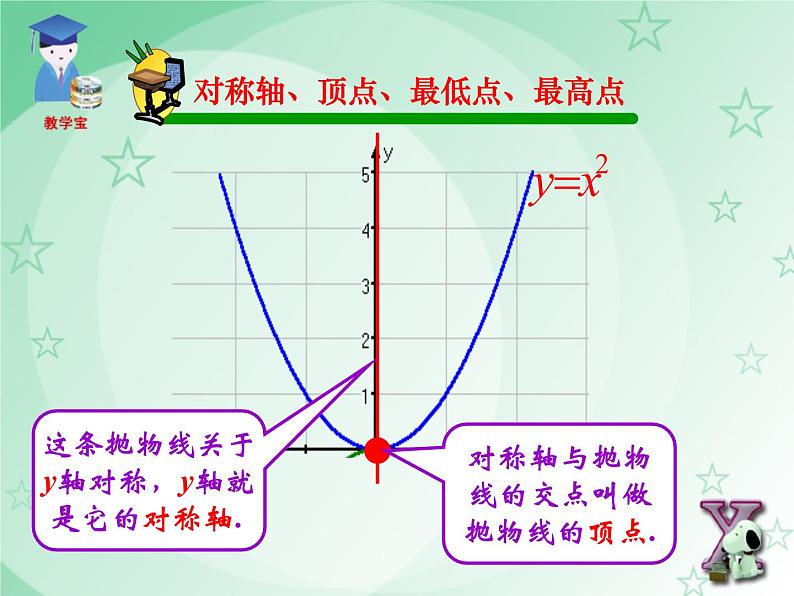
这条抛物线关于y轴对称，y轴就 是它的对称轴.
对称轴、顶点、最低点、最高点
对称轴与抛物线的交点叫做抛物线的顶点.
抛物线 y=x2在x轴上方(除顶点外)，顶点是它的最低点，开口向上，并且向上无限伸展; 当x=0时,函数 y的值最小，最小值是0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
抛物线 y= -x2在x轴下方(除顶点外)，顶点是它的最高点，开口向下，并且向下无限伸展，当x=0时，函数y的值最大，最大值是0.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
在x轴上方(除顶点外)
在x轴下方( 除顶点外)
当x=0时,最小值为0
当x=0时,最大值为0
y = x2、y= - x2
在同一坐标系中作二次函数y= x2和y=2x2的图象，会是什么样?
例1.在同一直角坐标系中画出函数y= x2和y=2x2的图像
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点?
a>0，开口都向上;对称轴都是y轴;增减性相同
只是开口大小不同二次项系数越大，开口越小
顶点都是原点(0,0)
在同一直角坐标系中画出函数y=－ x2和y=－2x2的图像
函数y=- x2,y=-2x2的图像与函数y=－x2(图中虚线图形)的图像相比,有什么共同点和不同点?
a < 0，开口都向下;对称轴都是y轴;增减性相同.
只是开口大小不同二次项系数越小，开口越小
一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.
当a>0时,抛物线的开口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小
当a<0时,抛物线的开口向上,顶点是抛物线的最高点,a越小,抛物线的开口越小;
在同一坐标系内,抛物线y=ax2与抛物线y=－ax2是关于x轴对称的.
1. 二次函数的图像都是抛物线.
2. 抛物线y=ax2的图像性质:
(2)当a>0时,抛物线的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
|a|越大,抛物线的开口越小;
(1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
1、函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
2、函数y=－3x2的图象的开口 ,对称轴 ,顶点是 ;
已知 y =(m+1)x 是二次函数且其图象开口向上,求m的值和函数解析式
m+1>0 ①
解②得:m1=－2, m2=1
此时,二次函数为: y=2x2,
请同学们把所学的二次函数图象的知识归纳小结。