高中数学人教A版 (2019)必修 第一册3.4 函数的应用（一）精练

这是一份高中数学人教A版 (2019)必修 第一册3.4 函数的应用（一）精练，共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

3.4函数的应用（一）
一、单选题
1．一家货物公司计划租地建造仓库储存货物，经市场调查了解到下列信息：每月土地占地费（单位：万元）与仓库到车站的距离（单位：）成反比，每月库存货物费（单位：万元）与成正比，若在距离车站处建仓库，则为万元，为万元，下列结论正确的是（    ）
A． B．
C．有最大值 D．无最小值
【答案】D
【分析】根据题意求出、关于的表达式，可判断AB选项的正误；利用基本不等式可判断C选项的正误；利用函数的单调性可判断D选项的正误.
【解析】对于A选项，设，可得，所以，，则，A错；
对于B选项，设，可得，所以，，则，B错；
对于C选项，因为，由基本不等式可得，
当且仅当时，等号成立，C错；
对于D选项，令，则函数在上为减函数，
故无最小值，D对.
故选：D.
2．某公司的收入由保险业务收入和理财业务收入两部分组成.该公司年总收入为亿元，其中保险业务收入为亿元，理财业务收入为亿元.该公司经营状态良好、收入稳定，预计每年总收入比前一年增加亿元.因越来越多的人开始注重理财，公司理财业务发展迅速.要求从年起每年通过理财业务的收入是前一年的倍，若要使得该公司年的保险业务收入不高于当年总收入的，则的值至少为（    ）
A． B． C． D．
【答案】A
【分析】求出年通过理财业务的收入为亿元，根据题意可得出关于的不等式，解出的范围即可得解.
【解析】因为该公司年总收入为亿元，预计每年总收入比前一年增加 亿元，所以年的总收入为亿元，
因为要求从年起每年通过理财业务的收入是前一年的倍，
所以年通过理财业务的收入为亿元，所以，解得.故的值至少为，
故选：A.
3．单位时间内通过道路上指定断面的车辆数被称为“道路容量”，与道路设施、交通服务、环境、气候等诸多条件相关.假设某条道路一小时通过的车辆数满足关系，其中为安全距离，为车速.当安全距离取时，该道路一小时“道路容量”的最大值约为（    ）
A．135 B．149
C．165 D．195
【答案】B
【分析】把给定函数变形，利用基本不等式即可得解.
【解析】由题意得，，当且仅当，即时取“=”，
所以该道路一小时“道路容量”的最大值约为149.
故选：B
4．某企业一个月生产某种商品万件时的生产成本为(万元)，一万件售价是30万元，若商品能全部卖出，则该企业一个月生产该商品的最大利润为（    ）
A．139万元 B．149万元 C．159万元 D．169万元
【答案】C
【分析】，然后利用二次函数的知识可得答案.
【解析】利润
故最大利润为159万元
故选：C
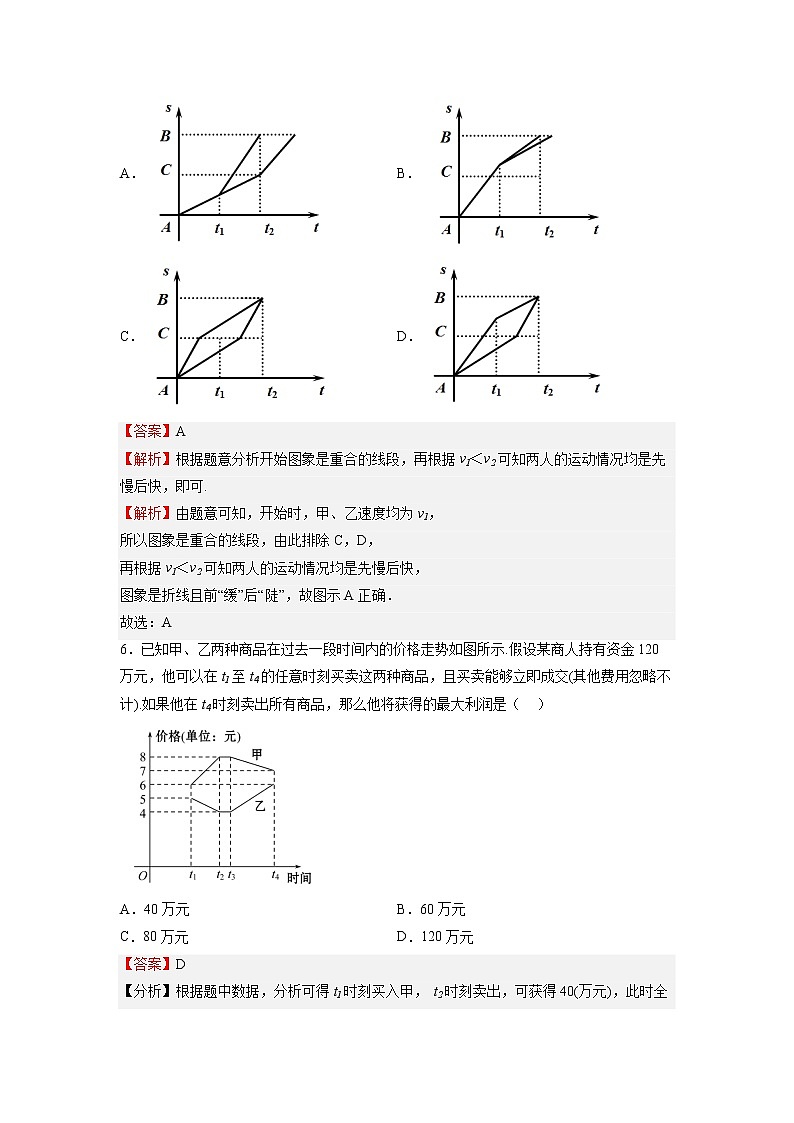
5．甲、乙两人沿着同一方向从地去地，甲前一半的路程使用速度，后一半的路程使用速度；乙前一半的时间使用速度，后一半的时间使用速度，关于甲，乙两人从地到达地的路程与时间的函数图象及关系（其中横轴表示时间，纵轴表示路程）可能正确的图示分析为（    ）
A． B．
C． D．
【答案】A
【解析】根据题意分析开始图象是重合的线段，再根据v1＜v2可知两人的运动情况均是先慢后快，即可.
【解析】由题意可知，开始时，甲、乙速度均为v1，
所以图象是重合的线段，由此排除C，D，
再根据v1＜v2可知两人的运动情况均是先慢后快，
图象是折线且前“缓”后“陡”，故图示A正确．
故选：A
6．已知甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某商人持有资金120万元，他可以在t1至t4的任意时刻买卖这两种商品，且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品，那么他将获得的最大利润是（    ）

A．40万元 B．60万元
C．80万元 D．120万元
【答案】D
【分析】根据题中数据，分析可得t1时刻买入甲， t2时刻卖出，可获得40(万元)，此时全部买入乙，并在t4时刻全部卖出，即可求得获得最大利润，即可得答案.
【解析】甲6元时，该商人全部买入甲商品，可以买120÷6=20(万份)，在t2时刻全部卖出，此时获利20×2=40(万元)，
乙4元时，该商人买入乙商品，可以买(120+40)÷4=40(万份)，在t4时刻全部卖出，此时获利40×2=80(万元)，共获利40+80=120(万元).
故选：D
7．周末，自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发分钟.乙骑行分钟后，甲以原速的继续骑行，经过一段时间，甲先到达地，乙一直保持原速前往地.在此过程中，甲、乙两人相距的路程（单位：米）与乙骑行的时间（单位：分钟）之间的关系如图所示，则下列说法错误的是（    ）

A．乙的速度为米/分钟 B．分钟后甲的速度为米/分钟
C．乙比甲晚分钟到达地 D．、两地之间的路程为米
【答案】C
【分析】首先由图象确定甲乙两人的速度，再求出甲到达地时乙距离的的距离，计算甲的总路程即为、两地之间的路程，进而可判断各个选项的正确性，即可得正确答案.
【解析】因为乙比甲早出发分钟，由图知：乙的速度为米/分钟，故选项A正确；
设甲的原速度为，因为，解得：米/分钟，
所以分钟后甲的速度为米/分钟，故选项B正确；
当时，甲到达地，此时乙距离地还有米，所以还需要分钟，所以乙比甲晚分钟到达地，故选项C
不正确；
、两地之间的路程为米，故选项D正确；
所以说法错误的是选项C，
故选：C.
8．新冠肺炎疫情防控中，核酸检测是新冠肺炎确诊的有效快捷手段．某医院在成为新冠肺炎核酸检测定点医院并开展检测工作的第天，每个检测对象从接受检测到检测报告生成平均耗时（单位：小时）大致服从的关系为（、为常数）.已知第天检测过程平均耗时为小时，第天和第天检测过程平均耗时均为小时，那么可得到第天检测过程平均耗时大致为（    ）
A．小时 B．小时 C．小时 D．小时
【答案】C
【解析】根据题意求得和的值，然后计算出的值即可得解.
【解析】由第天和第天检测过程平均耗时均为小时知，，
所以，得．
又由知，，所以当时，，
故选：C．
【点睛】本题考查分段函数模型的应用，求出和的值是解题的关键，考查计算能力，属于中等题.

二、多选题
9．在一次社会实践活动中，某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量（单位：千克）与时间（单位：小时）的函数图像，则以下关于该产品生产状况的正确判断是.

A．在前三小时内，每小时的产量逐步增加
B．在前三小时内，每小时的产量逐步减少
C．最后一小时内的产量与第三小时内的产量相同
D．最后两小时内，该车间没有生产该产品
【答案】BD
【分析】根据车间持续5个小时的生产总产量（单位：千克）与时间（单位：小时）的函数图像，分别进行判断即可．
【解析】由该车间持续5个小时的生产总产量（单位：千克）与时间（单位：小时）的函数图像，得：前3小时的产量逐步减少，故A错，B正确；
后2小时均没有生产，故C错，D正确．
故选BD
【点睛】此题考查函数图像的实际应用，关键点是将函数图像和实际问题联系起来，属于较易问题．
10．已知每生产100克饼干的原材料加工费为1.8元，某食品加工厂对饼干采用两种包装，其包装费用、销售价格如表所示：
型号
小包装
大包装
质量
100克
300克
包装费
0.5元
0.7元
销售价格
3.00元
8.4元

则下列说法正确的是（    ）A．买小包装实惠
B．买大包装实惠
C．卖3小包比卖1大包盈利多
D．卖1大包比卖3小包盈利多
【答案】BD
【分析】根据题中数据，可换算出每100克的售价，比较即可判断A、B的正误；分别算出卖1大包的盈利和卖3小包的盈利，比较即可判断C、D的正误，即可得答案.
【解析】大包装300克8.4元，则等价为100克2.8元，小包装100克3元，则买大包装实惠，故B正确，
卖1大包的盈利8.4-0.7-1.8×3=2.3(元)，卖1小包盈利3-0.5-1.8=0.7(元)，则卖3小包盈利0.7×3=2.1(元)，则卖1大包比卖3小包盈利多，故D正确.
故选：BD
11．几名大学生创业时经过调研选择了一种技术产品，生产此产品获得的月利润（单位：万元）与每月投入的研发经费（单位：万元）有关.已知每月投入的研发经费不高于16万元，且，利润率.现在已投入研发经费9万元，则下列判断正确的是（    ）
A．此时获得最大利润率 B．再投入6万元研发经费才能获得最大利润
C．再投入1万元研发经费可获得最大利润率 D．再投入1万元研发经费才能获得最大利润
【答案】BC
【分析】结合题目中所给条件及自变量的实际意义，利用二次函数以及基本不等式进行求解.
【解析】当时，，
故当时，获得最大利润，为，故B正确，D错误；
，
当且仅当，即时取等号，此时研发利润率取得最大值2，故C正确，A错误.
故选：BC.
12．(多选)某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，先收取固定的制版费，再按印刷数量收取印刷费，乙厂直接按印刷数量收取印刷费，甲厂的总费用y1(千元)､乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲､乙所示，则（    ）

A．甲厂的制版费为1千元，印刷费平均每个为0.5元
B．甲厂的总费用y1与证书数量x之间的函数关系式为
C．当印制证书数量不超过2千个时，乙厂的印刷费平均每个为1.5元
D．当印制证书数量超过2千个时，乙厂的总费用y2与证书数量x之间的函数关系式为
【答案】ABCD
【分析】根据甲厂和乙厂的函数图象，结合一次函数的图象与性质，结合待定系数法，即可求解.
【解析】由题图知甲厂制版费为1千元，印刷费平均每个为0.5元，故A正确；
设甲厂的费用与证书数量满足的函数关系式为，
代入点，可得，解得，
所以甲厂的费用与证书数量满足的函数关系式为，故B正确；
当印制证书数量不超过2千个时，乙厂的印刷费平均每个为元，故C正确；
设当时，设与之间的函数关系式为
代入点，可得，解得，
所以当时，与之间的函数关系式为，故D正确.
故选：ABCD.

三、填空题
13．生产一定数量的商品的全部费用称为生产成本，某企业一个月生产某种商品万件时的生产成本为 (万元)．一万件售价为万元，为获取更大利润，该企业一个月应生产该商品数量为________万件．
【答案】
【解析】根据题意，可得利润=售价-成本，将利润表示出来，得到关于的二次函数，再根据二次函数性质求解最大值即可.
【解析】设利润为，则，当时，有最大值，
故答案为：18.
【点睛】本题是函数的应用题，关键是建立函数的关系式求解，解函数应用题，一般可按照以下步骤进行：
（1）读题：读懂和深刻理解题意，找出等量关系，将应用问题转化为数学问题；
（2）建模：把主要关系近似化、形式化，抽象成数学问题；
（3）求解：化归为常规问题，选择合适的数学方法求解；
（4）评价：对结果进行验证或评估，对错误加以调节，最终将结果应用于现实.
14．为了保护水资源，提倡节约用水，某城市对居民生活用水实行“阶梯水价”．计费方法如表所示，若某户居民某月交纳水费60元，则该月用水量_______m3．
每户每月用水量
水价
不超过12m3的部分
3元/m3
超过12m3但不超过18m3的部分
6元/m3
超过18m3的部分
9元/m3


【答案】16
【解析】由表格列出分段函数，再将水费代入求解对应用水量即可
【解析】设用数量为，交纳水费为，由题可知，当时，解得，
故答案为：16
【点睛】本题考查实际问题中函数模型的应用，属于基础题
15．某居民小区收取冬季供暖费，根据规定，住户可以从以下两种方案中任选其一：（1）按照使用面积缴纳，每平方米元；（2）按照建筑面积缴纳，每平方米元.李明家的使用面积为平方米.如果他家选择第（2）种方案缴纳供暖费较少，那么它的建筑面积最多不超过_______平方米.
【答案】
【分析】设李明家建筑面积为平方米，分别求出两种方案所需费用，再根据选择第（2）种方案缴纳供暖费较少，列出不等式，即可得出答案.
【解析】解：设李明家建筑面积为平方米，
按方案（1），李明家需缴元，
按方案（2），李明家需缴元，
因为选择第（2）种方案缴纳供暖费较少，
则，解得，
所以它的建筑面积最多不超过80平方米.
故答案为：80.
16．现在有红豆、白豆各若干粒.甲乙两人为了计算豆子的粒数，选用了这样的方法：第一轮甲每次取粒红豆，乙每次取粒白豆，同时进行，当红豆取完时，白豆还剩粒；第二轮，甲每次取粒红豆，乙每次取粒白豆，同时进行，当白豆取完时，红豆还剩粒.则红豆和白豆共有________粒.
【答案】
【分析】设红豆有粒，白豆有粒，由两轮的结果可构造方程组，根据的范围可计算求得，加和即可得到结果.
【解析】设红豆有粒，白豆有粒，
由第一轮结果可知：，整理可得：；
由第二轮结果可知：，整理可得：；
当时，由得：（舍）；
当时，由得：（舍）；
当时，由得：，，
即红豆和白豆共有粒.
故答案为：.

四、解答题
17．如图，某灌溉渠的横断面是等腰梯形，底宽2m，渠深为1.8m，斜坡的倾斜角是45°（无水状态不考虑）.


(1)试将横断面中水的面积（）表示成水深（m）的函数；
(2)当水深为1.2m时，求横断面中水的面积.
【答案】(1)
(2)3.84

【分析】（1）根据给定条件利用梯形的面积公式列式化简即得.
（2）由（1）得出的函数的解析式，代入计算可得答案.
（1）
依题意，横断面中的水面是下底为2m，上底为m，高为h m的等腰梯形，    
所以.
（2）
由（1）知，，，
所以当水深为1.2m时，横断面水中的面积为3.84.
18．“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，把每尾鱼的平均生长速度v（单位：千克/年）表示为养殖密度x（单位：尾/立方米）的函数.当时，v的值为2；当时，v是关于x的一次函数.当x＝20时，因缺氧等原因，v的值为0.
(1)当时，求函数的表达式；
(2)当x为多大时，鱼的年生长量（单位：千克/立方米）可以达到最大？并求出最大值.
【答案】(1)
(2)x＝10，最大值为12.5千克/立方米

【分析】（1）根据题意得建立分段函数模型求解即可；
（2）分段求得函数的最值，比较可得答案.
（1）
依题意，当时，；
当时，是关于x的一次函数，假设，
则，解得，
所以.
（2）
当时，；
当时，，
当时，取得最大值.
因为，所以当x＝10时，鱼的年生长量可以达到最大，最大值为12.5.
19．首届世界低碳经济大会在南昌召开，本届大会以“节能减排，绿色生态”为主题.某单位在国家科研部门的支持下进行技术攻关，采取了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本 (元)与月处理量 (吨)之间的函数关系可近似的表示为 ，且处理每吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
(2)该单位每月能否获利？如果获利，求出最大利润；如果不获利，则需要国家至少补贴多少元才能使单位不亏损？
【答案】(1)400吨；
(2)不获利，需要国家每个月至少补贴40000元才能不亏损.

【分析】（1）由题设平均每吨二氧化碳的处理成本为，应用基本不等式求其最小值，注意等号成立条件.
（2）根据获利，结合二次函数的性质判断是否获利，由其值域确定最少的补贴额度.
（1）
由题意知，平均每吨二氧化碳的处理成本为；
当且仅当 ，即 时等号成立，
故该当每月处理量为400吨时，才能使每吨的平均处理成本最低为200元.
（2）
不获利，设该单位每个月获利为S元，则 ，
因为，则，
故该当单位每月不获利，需要国家每个月至少补贴40000元才能不亏损.
20．吉祥物“冰墩墩”在北京2022年冬奥会强势出圈，并衍生出很多不同品类的吉祥物手办．某企业承接了“冰墩墩”玩具手办的生产，已知生产此玩具手办的固定成本为200万元．每生产万盒，需投入成本万元，当产量小于或等于50万盒时；当产量大于50万盒时，若每盒玩具手办售价200元，通过市场分析，该企业生产的玩具手办可以全部销售完（利润＝售价－成本，成本＝固定成本＋生产中投入成本）
(1)求“冰墩墩”玩具手办销售利润（万元）关于产量（万盒）的函数关系式；
(2)当产量为多少万盒时，该企业在生产中所获利润最大？
【答案】(1)
(2)70万盒

【分析】（1）根据题意分和两种情况求解即可；
（2）根据分段函数中一次与二次函数的最值求解即可.
（1）
当产量小于或等于50万盒时，，
当产量大于50万盒时，，
故销售利润（万元）关于产量（万盒）的函数关系式为

（2）
当时，；
当时，，
当时，取到最大值，为1200．                    
因为，所以当产量为70万盒时，该企业所获利润最大．
21．随着城市居民汽车使用率的增加，交通拥堵问题日益严重，而建设高架道路、地下隧道以及城市轨道公共运输系统等是解决交通拥堵问题的有效措施.某市城市规划部门为提高早晚高峰期间某条地下隧道的车辆通行能力，研究了该隧道内的车流速度（单位：千米/小时）和车流密度（单位：辆/千米）所满足的关系式：.研究表明：当隧道内的车流密度达到120辆/千米时造成堵塞，此时车流速度是0千米/小时.
(1)若车流速度不小于40千米/小时，求车流密度的取值范围；
(2)隧道内的车流量（单位时间内通过隧道的车辆数，单位：辆/小时）满足，求隧道内车流量的最大值（精确到1辆/小时），并指出当车流量最大时的车流密度（精确到1辆/千米）.（参考数据：）
【答案】(1)车流密度的取值范围是
(2)隧道内车流量的最大值约为3667辆/小时，此时车流密度约为83辆/千米.

【分析】（1）根据题意得，再根据分段函数解不等式即可得答案；
（2）由题意得，再根据基本不等式求解最值即可得答案.
（1）
解：由题意知当（辆/千米）时，（千米/小时），
代入，解得，
所以.
当时，，符合题意；
当时，令，解得，所以.
所以，若车流速度不小于40千米/小时，则车流密度的取值范围是.
（2）
解：由题意得，
当时，为增函数，所以，当时等号成立；
当时，
.
当且仅当，即时等号成立.
所以，隧道内车流量的最大值约为3667辆/小时，此时车流密度约为83辆/千米.
22．某公司对两种产品A，B的分析如下表所示：
产品类别
年固定成本
每件产品成本
每件产品销售价格
每年最多可生产的件数
A
20万元
m万元
10万元
200件
B
40万元
8万元
18万元
120件

其中年固定成本与年生产的件数无关，m为常数，且．另外，销售A产品没有附加税，年销售x件，B产品需上交万元的附加税．假定生产出来的产品都能在当年销售出去，并且该公司只选择一种产品进行投资生产．
（1）求出该公司分别投资生产A，B两种产品的年利润（单位：万元）与年生产相应产品的件数x之间的函数解析式，并指出定义域；
（2）分别求出投资生产这两种产品的最大年利润，比较最大年利润，决定投资方案，该公司投资生产哪种产品可获得最大年利润？
【答案】（1），其中；，其中；（2）答案见解析．
【分析】（1）利润等于单件产品的盈利与件数的乘积；（2）分别根据函数的类型确定单调性求出最大值，作差比较二者大小即得．
【解析】（1），其中
，其中
（2）∵，∴，∴在定义域上是增函数
∴当时，
又，∴当时，

当时，即时，投资A产品可获得最大年利润．
当时，即时，投资A或B产品可获得最大年利润．
当时，即时，投资B产品可获得最大年利润．
23．如图，某日的钱塘江观测信息如下：2017年月日，天气：阴；能见度：1.8千米；时，甲地“交叉潮”形成，潮水匀速奔向乙地；时，潮头到达乙地，形成“一线潮”，开始均匀加速，继续向西；时，潮头到达丙地，遇到堤坝阻挡后回头，形成“回头潮”.

按上述信息，小红将“交叉潮”形成后潮头与乙地质检的距离（千米）与时间（分钟）的函数关系用图3表示.其中：“时甲地‘交叉潮’的潮头离乙地12千米”记为点，点坐标为，曲线可用二次函数：，是常数）刻画.
(1)求值，并求出潮头从甲地到乙地的速度；
(2)时，小红骑单车从乙地出发，沿江边公路以0.48千米分的速度往甲地方向去看潮，问她几分钟与潮头相遇？
(3)相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为0.48千米分，小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度，是加速前的速度）
【答案】(1)，千米分钟；
(2)小红5分钟后与潮头相遇；
(3)小红与潮头相遇到潮头离她1.8千米外共需26分钟.

【分析】（1）根据给定时间及坐标系求出m，再计算速度作答.
（2）求出小红从乙地出发时潮头离乙地的距离，设出从出发到与潮头相遇的时间，列方程求解作答.
（3）根据给定数据求出s与t的函数关系，求出小红追赶潮头距离乙地的距离与t的关系，由相距1.8千米列出方程，求解作答.
（1）
到的时间是30分钟，则，即，
潮头从甲地到乙地的速度（千米分钟）.
（2）
因潮头的速度为0.4千米分钟，则到时，潮头已前进（千米），
此时潮头离乙地（千米），设小红出发分钟与潮头相遇，
于是得，解得，
所以小红5分钟后与潮头相遇.
（3）
把，代入，得，解得，，
因此，又，则，
当潮头的速度达到单车最高速度0.48千米分，即时，，解得，
则当时，，
即从分钟时）开始，潮头快于小红速度奔向丙地，小红逐渐落后，但小红仍以0.48千米分的速度匀速追赶潮头，
设小红离乙地的距离为，则与时间的函数关系式为，
当时，，解得：，因此有，
最后潮头与小红相距1.8千米，即时，有，
解得，（舍去），
于是有，小红与潮头相遇后，按潮头速度与潮头并行到达乙地用时（分钟），
因此共需要时间为（分钟），
所以小红与潮头相遇到潮头离她1.8千米外共需26分钟.