初中数学人教版九年级下册27.3 位似第2课时教案设计

这是一份初中数学人教版九年级下册27.3 位似第2课时教案设计，共10页。教案主要包含了教学目标，重点难点，设计思路，教学过程设计等内容，欢迎下载使用。
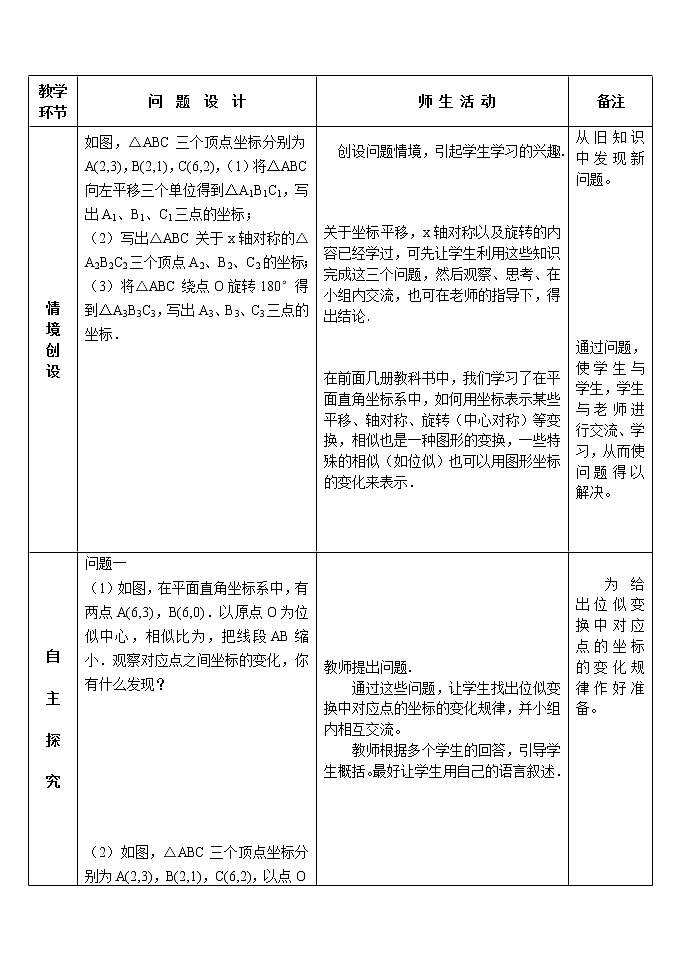
27.3 .2位似（第2课时） 一、教学目标知识与技能  会用图形的坐标的变化来表示图形的位似变换。  掌握把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律．过程与方法1．了解位似图形的四种变换，即：平移、轴对称、旋转和位似，并找出它们之间的异同。2．让学生能在复杂图形中找出这四种变换．情感态度与价值观1. 在获得知识的过程中培养学习的自信心．                                                                                                                                                                                                                                                                                                                                                                                                    2. 敢于面对数学活动中的困难，并能有意识地运用已有知识解决新问题.二、重点难点重点用图形的坐标的变化来表示图形的位似变换．难点   把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律．                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                             四、教学过程设计 教学环节问  题  设  计师 生 活 动备注情境创设如图，△ABC三个顶点坐标分别为A(2,3)，B(2,1)，C(6,2)，（1）将△ABC向左平移三个单位得到△A1B1C1，写出A1、B1、C1三点的坐标；（2）写出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标；（3）将△ABC绕点O旋转180°得到△A3B3C3，写出A3、B3、C3三点的坐标．         创设问题情境，引起学生学习的兴趣.   关于坐标平移，x轴对称以及旋转的内容已经学过，可先让学生利用这些知识完成这三个问题，然后观察、思考、在小组内交流，也可在老师的指导下，得出结论.  在前面几册教科书中，我们学习了在平面直角坐标系中，如何用坐标表示某些平移、轴对称、旋转（中心对称）等变换，相似也是一种图形的变换，一些特殊的相似（如位似）也可以用图形坐标的变化来表示．从旧知识中发现新问题。         通过问题，使学生与学生，学生与老师进行交流、学习，从而使问题得以解决。自 主 探 究问题一（1）如图，在平面直角坐标系中，有两点A(6,3)，B(6,0)．以原点O为位似中心，相似比为，把线段AB缩小．观察对应点之间坐标的变化，你有什么发现？      （2）如图，△ABC三个顶点坐标分别为A(2,3)，B(2,1)，C(6,2)，以点O为位似中心，相似比为2，将△ABC放大，观察对应顶点坐标的变化，你有什么发现？  问题二：1、如图，四边形ABCD的坐标分别为A（－6，6），B（－8，2），C（－4，0），D（－2，4），画出它的一个以原点O为位似中心，相似比为  的位似图形．2、在下图所示的图案中，你能找出平移、轴对称、旋转和位似这些变换吗？        3、平移、轴对称、旋转和位似四种变换的异同      教师提出问题.通过这些问题，让学生找出位似变换中对应点的坐标的变化规律，并小组内相互交流。教师根据多个学生的回答，引导学生概括。最好让学生用自己的语言叙述．     让学生认真读题，按照题目的要求进行解答。 学生先各自独立思考，然后跟同组的同学一起讨论，交流结果。  【归纳】 位似变换中对应点的坐标的变化规律：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．   教材给出一种解法，让学生考虑能否还有其他解法。 解法二：点A的对应点A′′的坐标为[-6×，6×]，即A′′（3，-3）．类似地，可以确定其他顶点的坐标．（具体解法与作图略）      分析：观察的角度不同，答案就不同．如：它可以看作是一排鱼顺时针旋转45°角，连续旋转八次得到的旋转图形；它还可以看作位似中心是图形的正中心，相似比是4∶3∶2∶1的位似图形，……解：答案不惟一平移、轴对称、旋转和位似四种变换的异同：图形经过平移、旋转或轴对称的变换后，虽然对应位置改变了，但大小和形状没有改变，即两个图形是全等的；而图形放大或缩小（位似变换）之后是相似的． 为给出位似变换中对应点的坐标的变化规律作好准备。          学生通过学习,得出位似变换中对应点的坐标的变化规律。      关注学生是否能主动参与探究活动,鼓励学说积极地表达自己的观点.     通过对问题让学生进一步领会从不同角度解决问题的思想，培养学生从多角度思考问题，为他们以后更好地学习新知识作准备..    尝 试 应 用1．（2009年福州）如图，正五边形FGHMN是由正五边形ABCDE经过位似变换得到的，若AB:FG=2:3，则下列结论正确的是（  ）A．2DE=3MN，        B．3DE=2MN，      C．3∠A=2∠F     D．2∠A=3∠F 2. (2010年福建省德化县)如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”上一个“顶点”的坐标为，那么大“鱼”上对应“顶点”的坐标为   （  ）Ａ、Ｂ、Ｃ、Ｄ、      3、如图，ABC三个顶点坐标分别为A(1，一l)．B(2，一3)，C(3，一l)，以原点0为位似中心，相似比为2，将ABC放大，位似变换后Ａ、Ｂ、C的对应点为    ．　　，　；　　，　　，　　      学生独立思考、解答.学生解答完毕后，小组交流后以小组为单位展示小组的成果。教师应关注：（1）       学生是否掌握经过位似变换的两图形相似；       （2）       学生能否识别图形，看出两位似图形是以原点为位似中心，相似比为-k。          由学生口答，要求学生能说出理由。 通过练习巩固和加深学生对这种知识的认识并加深理解. 成果展示中肯定学生的表现，并给出正确的答案  补 偿 提 高1．（2009年山西省）如图，与是位似图形，且顶点都在格点上，则位似中心的坐标是             ． 2、如图，图中的小方格都是边长为l的正方形，△ ABC与△是关于点0为位似中心的位似图形，它们的顶点都在小正方形的顶点上． (1)画出位似中心点0； (2)求出ABC与△的相似比； (3)以点0为位似中心，再画一个△，使它与ABC的相似比等于l．5．    教师出示题目:  学生练习时,教师巡视、辅导，了解学生的掌握情况.  重点关注学生对位似图形变换的概念和理解，以及对相似性它们之间的差异与联系的认识。         由学生自己动手画图，看学生的操作能力和实践能力。   学生在讨论中能否发表自己的见解，倾听他人的意见，并从中获益。    小结与作业小结：通过这节课的学习，你有哪些收获？  作业：1．教材P62．1、2， P64．习题27.32．如图，将图中的△ABC以A为位似中心，放大到1.5倍，请画出图形，并指出三个顶点的坐标所发生的变化．        教师提出问题.学生独立回答，教师在学生总结后,进行补充. 并根据学生的回答，总结本节知识.  教师布置作业，动员分层要求。学生按要求课外完成.  学生通过课后作业巩固本节知识. 使学生能回顾、总结、梳理所学知识. 教后反思    五、设计思路本节课开始创设一个坐标平移的问题作为情境，引起学生的学习兴趣和引出本课主题.通过两个具体题目，带领学生共同探究出位似变换中对应点的坐标的变化规律：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k． 本节课的最后要给学生总结（或让学生自己总结）平移、轴对称、旋转和位似四种变换的异同：图形经过平移、旋转或轴对称的变换后，虽然对应位置改变了，但大小和形状没有改变，即两个图形是全等的；而图形放大或缩小（位似变换）之后是相似的．并让学生练习在所给的图案中，找出平移、轴对称、旋转和位似这些变换．                              27.3 2位似（第2课时） 一、教学目标知识与技能  会用图形的坐标的变化来表示图形的位似变换。  掌握把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律．过程与方法1．了解位似图形的四种变换，即：平移、轴对称、旋转和位似，并找出它们之间的异同。2．让学生能在复杂图形中找出这四种变换．情感态度与价值观1. 在获得知识的过程中培养学习的自信心．                                                                                                                                                                                                                                                                                                                                                                                                    2. 敢于面对数学活动中的困难，并能有意识地运用已有知识解决新问题.二、重点难点重点用图形的坐标的变化来表示图形的位似变换．难点   把一个图形按一定大小比例放大或缩小后，点的坐标变化的规律．          三、教学过程设计问题一（1）如图，在平面直角坐标系中，有两点A(6,3)，B(6,0)．以原点O为位似中心，相似比为，把线段AB缩小．观察对应点之间坐标的变化，你有什么发现？   （2）如图，△ABC三个顶点坐标分别为A(2,3)，B(2,1)，C(6,2)，以点O为位似中心，相似比为2，将△ABC放大，观察对应顶点坐标的变化，你有什么发现？      问题二：1、如图，四边形ABCD的坐标分别为A（－6，6），B（－8，2），C（－4，0），D（－2，4），画出它的一个以原点O为位似中心，相似比为  的位似图形．          2、在下图所示的图案中，你能找出平移、轴对称、旋转和位似这些变换吗？3、平移、轴对称、旋转和位似四种变换的异同二、练习1．（2009年福州）如图，正五边形FGHMN是由正五边形ABCDE经过位似变换得到的，若AB:FG=2:3，则下列结论正确的是（  ）A．2DE=3MN，      B．3DE=2MN，     C．3∠A=2∠F     D．2∠A=3∠F2. (2010年福建省德化县)如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”上一个“顶点”的坐标为，那么大“鱼”上对应“顶点”的坐标为   （  ）Ａ、Ｂ、Ｃ、Ｄ、3、如图，ABC三个顶点坐标分别为A(1，一l)．B(2，一3)，C(3，一l)，以原点0为位似中心，相似比为2，将ABC放大，位似变换后Ａ、Ｂ、C的对应点为    ．　　，　； 三、测试1．（2009年山西省）如图，与是位似图形，且顶点都在格点上，则位似中心的坐标是             ．  2、如图，图中的小方格都是边长为l的正方形，△ ABC与△是关于点0为位似中心的位似图形，它们的顶点都在小正方形的顶点上． (1)画出位似中心点0； (2)求出ABC与△的相似比； (3)以点0为位似中心，再画一个△，使它与ABC的相似比等于l．5．