初中人教版21.2.4 一元二次方程的根与系数的关系教案

这是一份初中人教版21.2.4 一元二次方程的根与系数的关系教案，共3页。
*21.2.4　一元二次方程的根与系数的关系
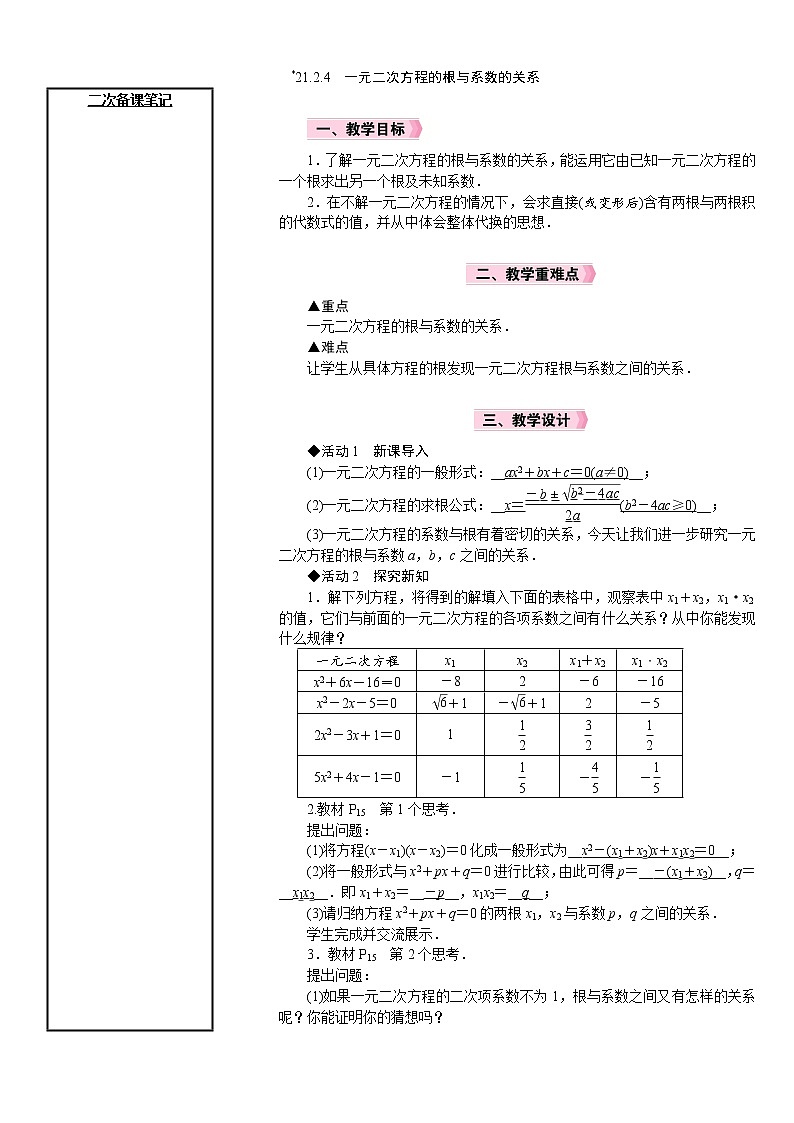
二次备课笔记    1．了解一元二次方程的根与系数的关系，能运用它由已知一元二次方程的一个根求出另一个根及未知系数．2．在不解一元二次方程的情况下，会求直接(或变形后)含有两根与两根积的代数式的值，并从中体会整体代换的思想． ▲重点一元二次方程的根与系数的关系．▲难点让学生从具体方程的根发现一元二次方程根与系数之间的关系． ◆活动1　新课导入(1)一元二次方程的一般形式：__ax2＋bx＋c＝0(a≠0)__；(2)一元二次方程的求根公式：__x＝(b2－4ac≥0)__；(3)一元二次方程的系数与根有着密切的关系，今天让我们进一步研究一元二次方程的根与系数a，b，c之间的关系．◆活动2　探究新知1．解下列方程，将得到的解填入下面的表格中，观察表中x1＋x2，x1·x2的值，它们与前面的一元二次方程的各项系数之间有什么关系？从中你能发现什么规律？一元二次方程x1x2x1＋x2x1·x2x2＋6x－16＝0－82－6－16x2－2x－5＝0＋1－＋12－52x2－3x＋1＝015x2＋4x－1＝0－1－－2.教材P15　第1个思考．提出问题：(1)将方程(x－x1)(x－x2)＝0化成一般形式为__x2－(x1＋x2)x＋x1x2＝0__；(2)将一般形式与x2＋px＋q＝0进行比较，由此可得p＝__－(x1＋x2)__，q＝__x1x2__．即x1＋x2＝__－p__，x1x2＝__q__；(3)请归纳方程x2＋px＋q＝0的两根x1，x2与系数p，q之间的关系．学生完成并交流展示．3．教材P15　第2个思考．提出问题：(1)如果一元二次方程的二次项系数不为1，根与系数之间又有怎样的关系呢？你能证明你的猜想吗？  二次备课笔记  (2)由求根公式可知一元二次方程ax2＋bx＋c＝0(a≠0)，当b2－4ac≥0时，两根分别为x1＝，x2＝.观察两式右边，分母相同，分子是－b＋与－b－.两根之间通过什么计算才能得到更简洁的关系？x1＋x2＝__－__，x1x2＝____． (3)由此你能得出方程的两个根x1，x2和系数a，b，c有怎样的关系吗？把方程ax2＋bx＋c＝0(a≠0)的两边同时除以a，能否得出该结论？为什么？学生完成并交流展示． ◆活动3　知识归纳若x1，x2是一元二次方程ax2＋bx＋c＝0(a≠0)的两个根，则有x1＋x2＝－，x1x2＝.即：任何一个一元二次方程的根与系数的关系为：两个根的和等于__一次项系数与二次项系数的比的相反数__，两个根的积等于__常数项与二次项系数的比__．提出问题：(1)方程的根是由什么决定的？(2)在运用根与系数的关系解决具体问题时，是否需要考虑根的判别式Δ＝b2－4ac≥0呢？为什么？  ◆活动4　例题与练习例1　教材P16　例4. 例2　已知a，b为实数，且满足a2－2a－1＝0，b2－2b－1＝0，求＋的值．解：当a＝b时，＋＝2.当a≠b时，a，b可看作方程x2－2x－1＝0的两根，则a＋b＝2，ab＝－1，因此＋＝＝＝－6.因此＋的值为2或－6.  练习1．教材P16　练习．2．已知一元二次方程2x2－5x＋1＝0的两根为m，n，则m2＋n2＝____．3．设一元二次方程x2－7x＋3＝0的两根为x1，x2，则x1＋x2＝__7__，x1x2＝__3__，(x1－2)(x2－2)＝__－7__．   二次备课笔记   4．已知关于x的一元二次方程x2＋(2m－1)x＋m2＝0有两个实数根x1，x2.(1)求实数m的取值范围；(2)是否存在m使得x－x＝0成立？若存在，请求出m的值；若不存在，请说明理由．解：(1)∵原方程有两个实数根，∴Δ＝(2m－1)2－4m2＝4m2－4m＋1－4m2＝－4m＋1≥0，∴m≤；(2)假使存在实数m使得x－x＝0，∴x1＋x2＝0或x1＝x2.当x1＋x2＝0时，－(2m－1)＝0，∴m＝＞(舍)；当x1＝x2时，Δ＝0，∴m＝.◆活动5　课堂小结一元二次方程根与系数的关系：一元二次方程ax2＋bx＋c＝0(a≠0，b2－4ac≥0)的两根x1，x2和系数a，b，c有如下关系：x1＋x2＝－，x1x2＝.1．作业布置(1)教材P17　习题21.2第7题；(2)对应课时练习．2．教学反思