人教B版 (2019)必修第三册7.1.2 弧度制及其与角度制的换算评优课课件ppt

展开

这是一份人教B版 (2019)必修第三册7.1.2 弧度制及其与角度制的换算评优课课件ppt，文件包含712《弧度制及其与角度制的换算》课件PPTpptx、712《弧度制及其与角度制的换算》教案docx等2份课件配套教学资源，其中PPT共39页，欢迎下载使用。

1.了解角的另外一种度量方法——弧度制. 2.能进行弧度与角度的互化，体会引入弧度制的必要性.3.掌握弧度制中扇形的弧长公式和面积公式4.通过学习，提高学生数学抽象、数学运算的核心素养.
重点：弧度与角度的互化；难点：弧度角的概念的理解.
新知初探---自主预习
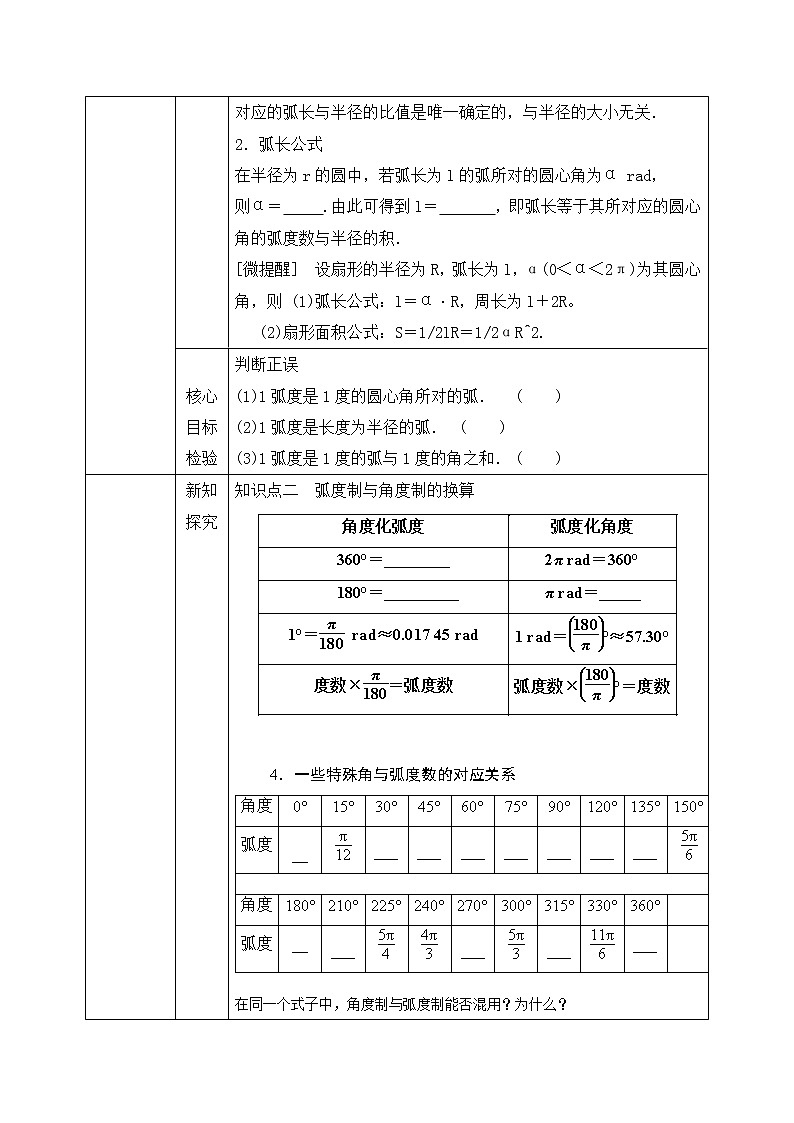
知识点一　弧度制1．度量角的两种制度(1)角度制：用作单位来度量角的制度称为角度制．规定1度等于分，1分等于秒．(2)弧度制：以为单位来度量角的制度称为弧度制．称弧长与半径比值的这个常数为圆心角的弧度数，长度等于半径长的圆弧所对的圆心角为1弧度的角，记作1 rad.
[微提醒]　今后在用弧度制表示角时，“弧度”二字或rad可以略去不写，而只写这个角的弧度数．
答：(1)定义不同．(2)单位不同．弧度制是以“弧度”为单位，单位可以省略，而角度制是以“度”为单位，单位不能省略．(3)弧度制是十进制，而角度制是六十进制．
“角度”与“弧度”的区别有哪些？
扇形的圆心角的弧度数随弧长和半径的改变而变化吗？
答：随着半径的变化，弧长也在变化，但对于一定大小的圆心角所对应的弧长与半径的比值是唯一确定的，与半径的大小无关．
2．弧长公式在半径为r的圆中，若弧长为l的弧所对的圆心角为α rad，则α＝ .由此可得到l＝，即弧长等于其所对应的圆心角的弧度数与半径的积．
判断正误(1)1弧度是1度的圆心角所对的弧．(　　)(2)1弧度是长度为半径的弧．(　　)(3)1弧度是1度的弧与1度的角之和．(　　)
知识点二　弧度制与角度制的换算
在同一个式子中，角度制与弧度制能否混用？为什么？
课堂探究---素养提升
题型一　角度制与弧度制的互化
进行角度制与弧度制互化的原则和方法
题型二　用弧度制表示终边相同的角
用弧度制表示终边相同的角2kπ＋α(k∈Z)时，其中2kπ是π的偶数倍，而不是整数倍，还要注意角度制与弧度制不能混用．
1．把－1 480°写成α＋2kπ(k∈Z)的形式，其中0≤α<2π.
题型三　扇形的面积与弧长的计算
(1)已知扇形的周长是6 cm，面积是2 cm2，求扇形的圆心角的弧度数．
(2)已知一扇形的圆心角是72°，半径等于20 cm，求扇形的面积．
弧度制下解决扇形相关问题的步骤
1．[圆心角的弧度数]已知扇形的周长为10 cm，面积为4 cm2，则扇形的圆心角α的弧度数为________．
3．[求扇形的半径]若扇形圆心角为216°，弧长为30π，则扇形半径为________．
4．[与最值有关的问题]已知扇形的周长为40 cm，则当它的半径和圆心角各取何值时，能使扇形的面积最大？最大面积是多少？
课堂小结---素养形成
1.一种角的度量方法——弧度制. 2.弧度与角度的互化.3.扇形的弧长公式和面积公式
解析：在弧度制下，终边相同的角相差2π的整数倍．故选C.
3．某扇形的半径为1 cm，它的周长为4 cm，那么该扇形的圆心角为________．
二、创新应用题5．已知集合A＝{α|2kπ<α<(2k＋1)π，k∈Z}，B＝{α|－5≤α≤5}，求A∩B.
解：由题意知，A＝…∪{α|－2π<α<－π}∪{α|0<α<π}∪{α|2π<α<3π}∪…，又B＝{α|－5≤α≤5}，两集合在数轴上的表示如图所示．∴A∩B＝{α|－5≤α<－π或0<α<π}．
三、易错防范题6．写出终边在如图所示阴影部分(不包括边界)内的角的集合 S＝_____________.
(1)本题易错处有两点：一是直接写成{α|k·360°＋330°<α

相关课件更多