数学八年级上册14.2 三角形全等的判定课堂教学ppt课件

这是一份数学八年级上册14.2 三角形全等的判定课堂教学ppt课件，共20页。PPT课件主要包含了全等三角形，判定方法，SAS，ASA，SSS，AAS，知识拓展，至少有一组边相等，AAASSA，直角三角形等内容，欢迎下载使用。

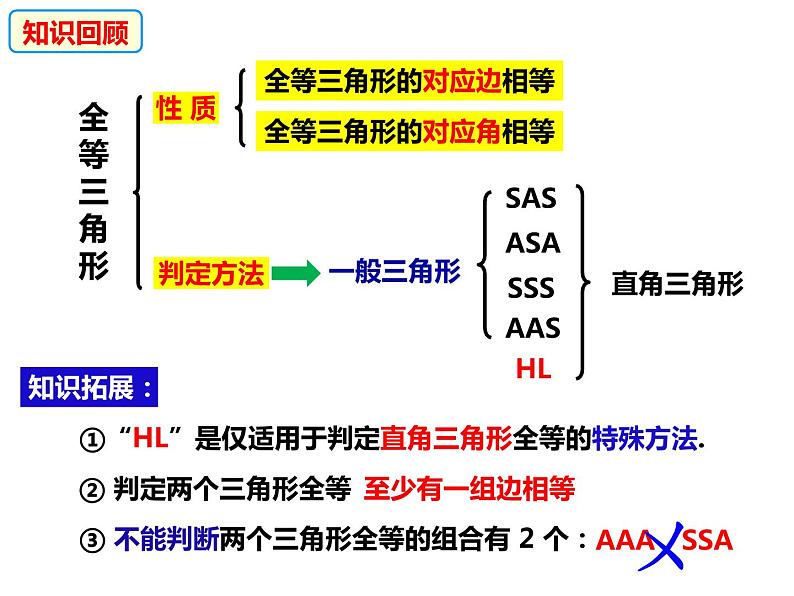
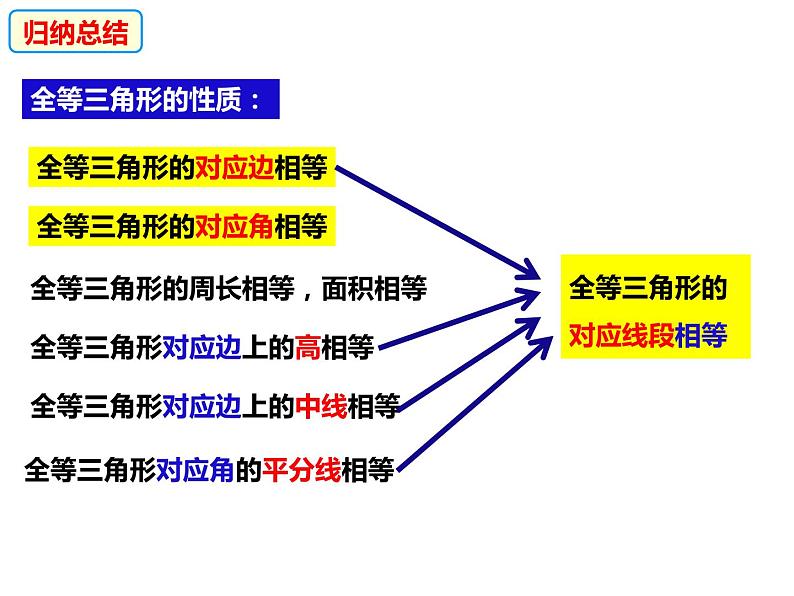
全等三角形的对应边相等
全等三角形的对应角相等
①“HL”是仅适用于判定直角三角形全等的特殊方法.
② 判定两个三角形全等
③ 不能判断两个三角形全等的组合有 2 个：
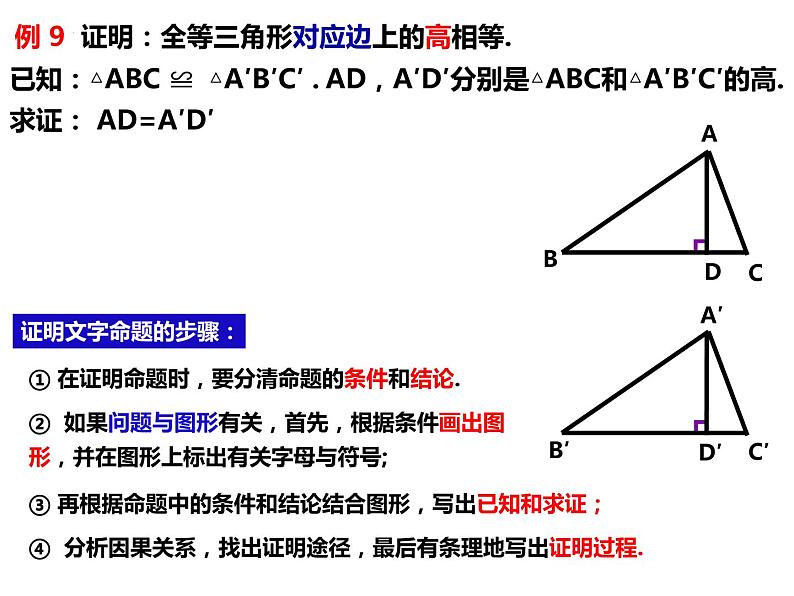
例 9 证明：全等三角形对应边上的高相等.
② 如果问题与图形有关，首先，根据条件画出图形，并在图形上标出有关字母与符号;
④ 分析因果关系，找出证明途径，最后有条理地写出证明过程.
③ 再根据命题中的条件和结论结合图形，写出已知和求证；
① 在证明命题时，要分清命题的条件和结论.
已知：△ABC ≌ △A′B′C′ .
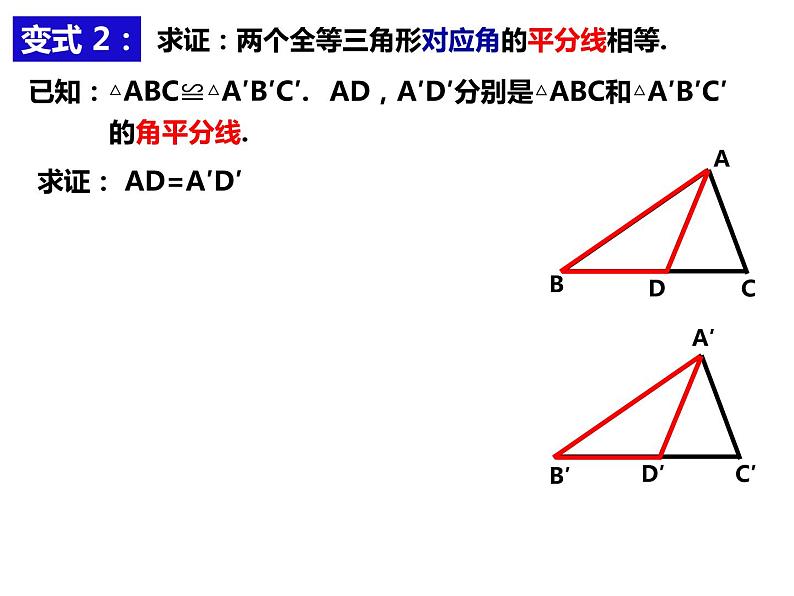
求证： AD=A′D′
AD，A′D′分别是△ABC和△A′B′C′的高.
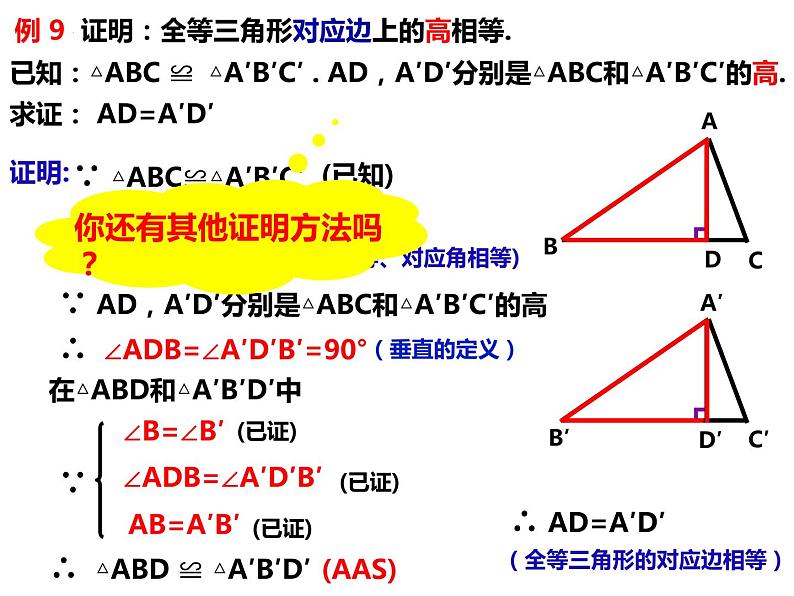
已知：△ABC ≌ △A′B′C′ . AD，A′D′分别是△ABC和△A′B′C′的高.
∵ △ABC≌△A′B′C′
(全等三角形的对应边相等、对应角相等)
∵ AD，A′D′分别是△ABC和△A′B′C′的高
∴ ∠ADB=∠A′D′B′=90°
在△ABD和△A′B′D′中
∠ADB=∠A′D′B′
∴ △ABD ≌ △A′B′D′
( 全等三角形的对应边相等 )
你还有其他证明方法吗？
∴ S△ABC=S△A′B′C′ ,
B′C′×A′D′
全等三角形面积相等，与高有关的问题可以用面积来解决.
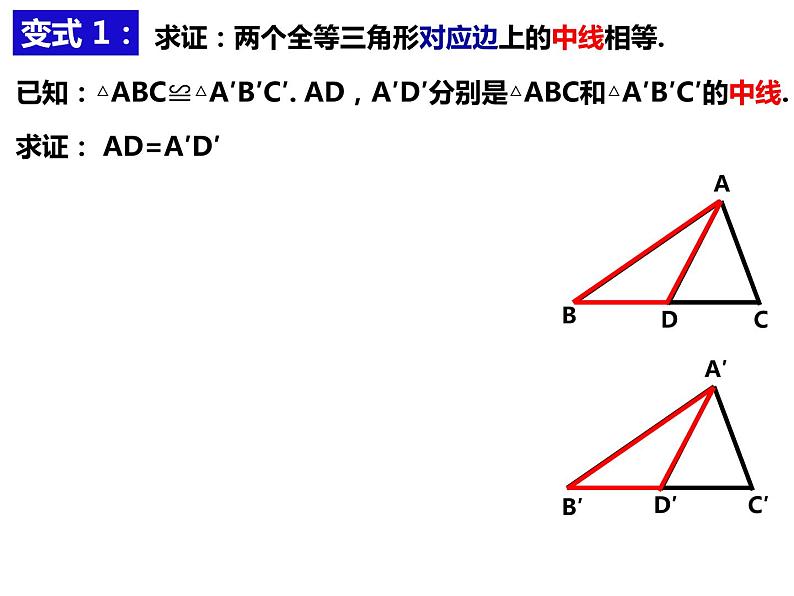
求证：两个全等三角形对应边上的中线相等.
已知：△ABC≌△A′B′C′.
AD，A′D′分别是△ABC和△A′B′C′的中线.
求证：两个全等三角形对应角的平分线相等.
AD，A′D′分别是△ABC和△A′B′C′的角平分线.
全等三角形对应角的平分线相等
全等三角形的周长相等，面积相等
全等三角形对应边上的高相等
全等三角形对应边上的中线相等
全等三角形的对应线段相等
1、已知：如图 AB=CD，BC=DA，E、F 是 AC 上的两点，且 AE=CF . 求证：BF=DE
2、如图，已知 AD，AF 分别是两个钝角 △ABC 和 △ABE 的高，如果 AD＝AF，AC＝AE. 求证：BC＝BE.
证明两个三角形全等的基本思路：
3、已知：如图，AB∥ CD，AB=CD，AD 与 BC 交于点 O，EF 过点 O，分别交 AB，CD 于点 E，点 F. 求证： OE=OF .
4、如图，已知 AB，CD 相交于点 O，AC∥ DB，OC=OD，E，F 为 AB 上两点，且 AE=BF，求证：CE=DF．
5、如图所示，CE⊥AB 于点E，BD⊥AC 于点 D，BD，CE 交于点O，且 AO 平分 ∠BAC． (1) 图中有多少对全等三角形？请一一列举出来. (2) 求证：BE=CD.
6、已知，如图，AB=AC，AD=AE，BD，CE 相交于点O.
(1) 求证： OD=OE .
(2) AO 平分 ∠BAC 吗？为什么？
7、如图，已知 Rt△ABC≌Rt△ADE，∠ABC=∠ADE=90°，BC 与 DE 相交于点 F，连接 CD，EB． (1) 图中还有几对全等三角形，请你一一列举； (2) 求证：CF=EF.
8、在四边形 ABCD 中，E 为 BC 边中点．已知：如图，若 AE 平分 ∠BAD，∠AED=90°，点 F 为 AD 上一点，AF=AB． 求证：(1) △ABE≌△AFE； (2) AD=AB+CD．