




八年级上册第14章 全等三角形14.2 三角形全等的判定课文ppt课件
展开到目前为止,我们学习了几种判定两个三角形全等的方法?
每一种判定方法都需要有
两边及其夹角分别相等的两个三角形全等
两角及其夹边分别相等的两个三角形全等
三边分别相等的两个三角形全等
除了配成 SAS,ASA,SSS,还可以配成哪些形式呢?
通过之前学习,我们知道,SAS,ASA,SSS 都可以作为判断两个三角形全等的条件.
那么请同学们想一想, 在三角形的六个基本元素中选择三个元素对应相等,
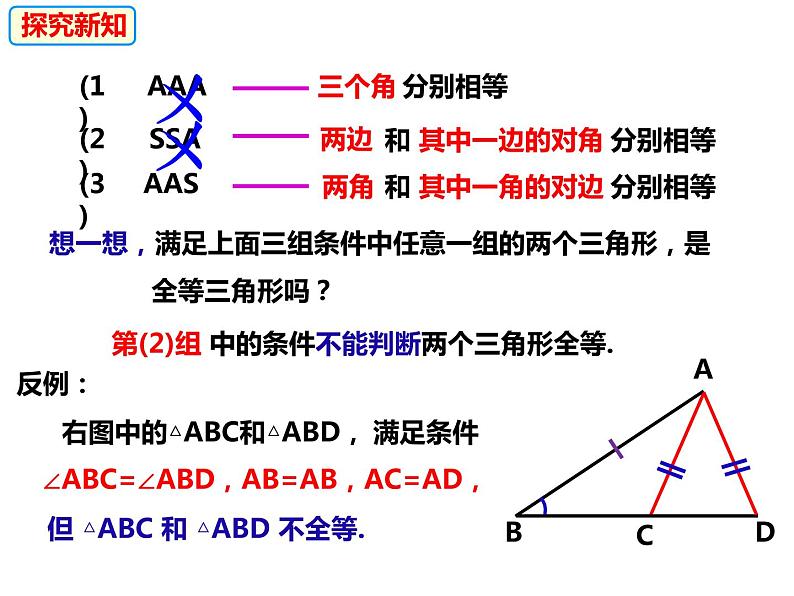
想一想,满足上面三组条件中任意一组的两个三角形,是 全等三角形吗?
只要举出一个反例即可.
第(1)组 中的条件不能判断两个三角形全等.
边长不等的两个等边三角形
但这两个等边三角形不全等.
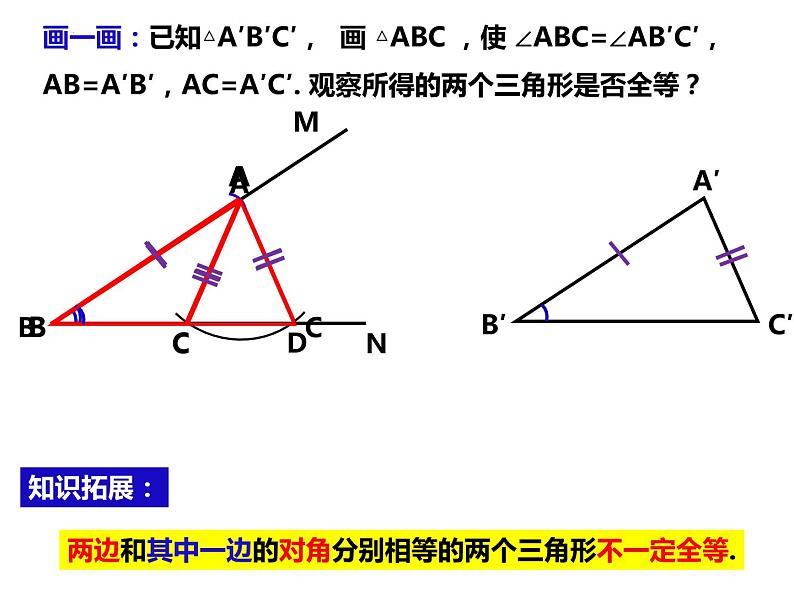
画一画:已知△A′B′C′, 画 △ABC ,使 ∠ABC=∠AB′C′,AB=A′B′,AC=A′C′. 观察所得的两个三角形是否全等?
两边和其中一边的对角分别相等的两个三角形不一定全等.
第(2)组 中的条件不能判断两个三角形全等.
∠ABC=∠ABD,AB=AB,AC=AD,
但 △ABC 和 △ABD 不全等.
右图中的△ABC和△ABD,
可以推得这两个三角形的第三个角也分别相等,
第(3)组 中的条件 能判断 两个三角形全等.
从而可以判定这样的两个三角形全等.
由三角形内角和等于180°,
这样AAS就可以转化成ASA,
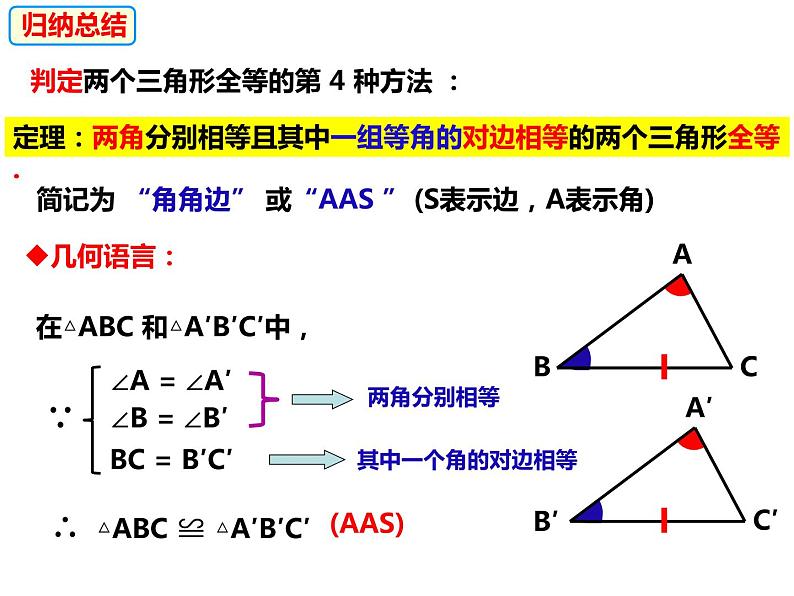
在△ABC 和△A′B′C′中,
∴ △ABC ≌ △A′B′C′
定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
判定两个三角形全等的第 4 种方法 :
(S表示边,A表示角)
BC = B′C′
那么就可以判定这两个三角形全等,
“ASA”与“AAS”的区别:
“边”是“其中一组等角的对边”.
”边“必须是”两角的夹边“;
依据“ASA”“AAS”.
可以判断两个三角形全等的组合有4个:
判定两个三角形全等的方法:
在两个三角形的六个元素中 (三条边和三个角),
SAS,ASA,SSS,AAS
不能判断两个三角形全等的组合有2个:
判定两个三角形全等至少有一组边相等.
例 6 已知,如图,点 B,F,C,D 在一条直线上,AB=ED, AB∥ ED,AC∥ EF. 求证:△ABC ≌ △EDF.
(两直线平行,内错角相等)
在 △ABC 和 △EDF 中
∴ △ABC ≌ △EDF
1、已知:如图,AB=AC,点D、E分别在AB、AC上,∠1=∠2 . 求证:DB=EC.
在△ABE和△ACD中
∴ △ABE ≌ △ACD
又 ∵ DB=AB-AD
(全等三角形的对应边相等)
2、如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是 。
3、如图,∠BAC=∠DAE,∠ABD=∠ACE,BD=CE. 求证:AB=AC.
∴ ∠BAC-∠DAC=∠DAE-∠DAC
即 ∠BAD=∠CAE
在 △ABD 和 △ACE 中
∴ △ABD ≌ △ACE
4、如图,∠A=∠B,AE=BE,点 D 在 AC 边上,∠1=∠2,AE 和 BD 相交于点 O.求证:△AEC≌△BED.
∵ ∠ADE=∠1+∠C
∴ ∠2+∠BDE=∠1+∠C
在 △AEC 和 △BDE 中
∴ △AEC≌△BED
5、如图,点 A,B,D,E 在同一直线上,AD=EB,BC∥ DF,∠C=∠F . 求证:AC=EF.
∴ AD-EF=EB-EF
∴ ∠CBD=∠FDB
又 ∵ ∠CBD+∠ABC=180°,
∠FDB+∠EDF=180°
∴ ∠ABC=∠EDF
6、如图,AD⊥AB 于点 A,BE⊥AB 于点 B,点 C 在 AB 上,且 CD⊥CE,CD=CE.求证:AD=CB.
∵ AD⊥AB,BE⊥AB
∴ ∠A=∠B=90°
∴ ∠D+∠ACD=90°
∴ ∠ACD+∠BCE=180°-90°=90°
在 △ACD 和 △BEC 中
∴ △ACD ≌ △BEC
7、在△ABC中,∠ACB=90°,AC=BC,直线 MN 经过点 C,且 AD⊥MN 于D,BE⊥MN 于 E.(1) 当直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;(2) 当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;(3) 当直线MN绕点C旋转到图(3)的位置时,请直接写出 DE, AD,BE 之间的等量关系,并加以证明.
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等.解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
8、在△ABC中,AB=AC,D、A、E 三点都在直线 m 上,并且有 ∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论 DE=BD+CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.
9、如图,已知在△ABC中,BC=AD,∠A=∠CDE=∠B. 求证:△ADE≌△BCD.
∵ ∠ADC=∠BCD+∠B
∴ ∠ADE+∠CDE=∠BCD+∠B
∴ ∠ADE=∠BCD
在 △ADE 和 △BCD 中
∴ △ADE≌△BCD
初中沪科版14.2 三角形全等的判定获奖课件ppt: 这是一份初中沪科版14.2 三角形全等的判定获奖课件ppt,共15页。PPT课件主要包含了CONTENTS,学习目标,新课导入,新课讲解,课堂小结,当堂小练,拓展与延伸,布置作业等内容,欢迎下载使用。
初中数学沪科版八年级上册14.2 三角形全等的判定习题ppt课件: 这是一份初中数学沪科版八年级上册14.2 三角形全等的判定习题ppt课件,共26页。PPT课件主要包含了角角边,AAS,不一定,①②③等内容,欢迎下载使用。
数学八年级上册14.2 三角形全等的判定课堂教学ppt课件: 这是一份数学八年级上册14.2 三角形全等的判定课堂教学ppt课件,共20页。PPT课件主要包含了全等三角形,判定方法,SAS,ASA,SSS,AAS,知识拓展,至少有一组边相等,AAASSA,直角三角形等内容,欢迎下载使用。













