沪科版八年级上册14.2 三角形全等的判定说课课件ppt

这是一份沪科版八年级上册14.2 三角形全等的判定说课课件ppt，共22页。PPT课件主要包含了连接CD如图所示，∴∠A∠B，∴DMDN，DCB，SAS，∠BAD∠CAD，ADAD，∴BDCD，变式1，变式2等内容，欢迎下载使用。

问题1 判定两个三角形全等除了定义以外，我们还学习了哪些方法？
(1)“SAS ”:两边及其夹角对应相等的两个三角形全等；
(2)“ASA ”:两角及其夹边对应相等的两个三角形全等；
(3)“SSS ”:三边对应相等的两个三角形全等；
(4)“AAS ”:两角及其一角对边对应相等的两个三角形全等；
(5)“HL ”:斜边和一直角边对应相等的两个直角三角形全等.
问题2 全等三角形有什么性质？
(1)全等三角形对应角相等、对应边相等；(2)全等三角形的面积、周长相等.
思考：结合全等三角形的性质及全等三角形的判定，你能说说如何证明两条线段（或角)相等？
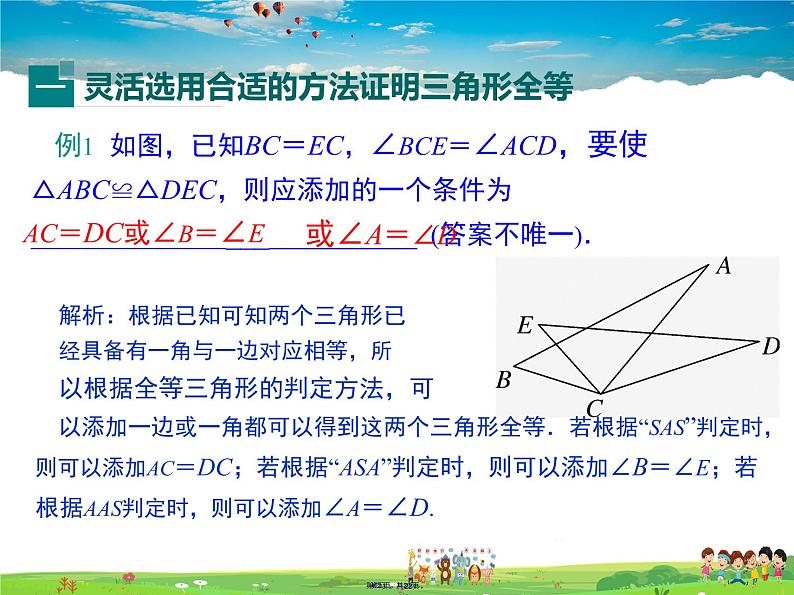
例1 如图，已知BC＝EC，∠BCE＝∠ACD，要使△ABC≌△DEC，则应添加的一个条件为_____________________________ (答案不唯一)．
解析：根据已知可知两个三角形已经具备有一角与一边对应相等，所以根据全等三角形的判定方法，可以添加一边或一角都可以得到这两个三角形全等．若根据“SAS”判定时，则可以添加AC＝DC；若根据“ASA”判定时，则可以添加∠B＝∠E；若根据AAS判定时，则可以添加∠A＝∠D.
AC＝DC或∠B＝∠E
（1）已知一边一角，可任意添加一个角的条件，用AAS或ASA判定全等；添加边的条件时只能添加夹这个角的边，用SAS判定全等．若添加另一边即这个角的对边，符合SSA的情形，不能判定三角形全等；（2）添加条件时，应结合判定图形和四种方法：SSS、SAS、ASA、AAS，注意不能是SSA的情形．
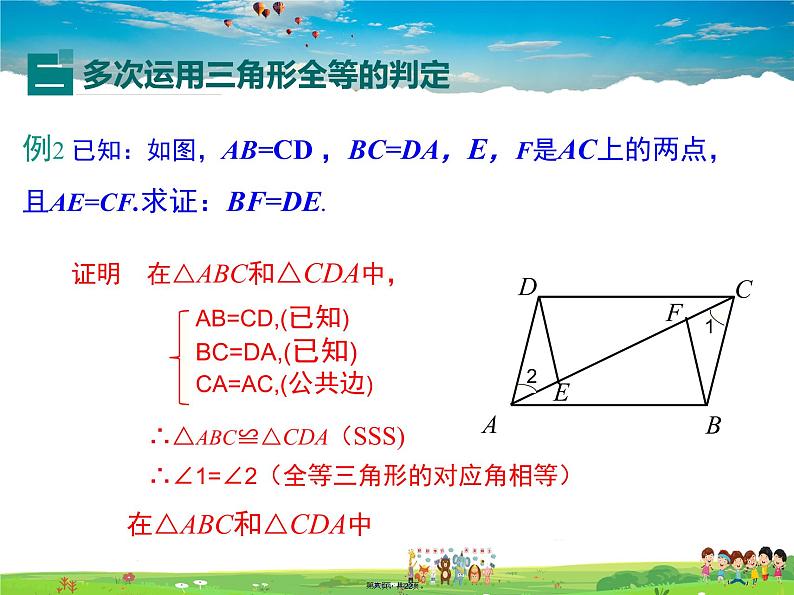
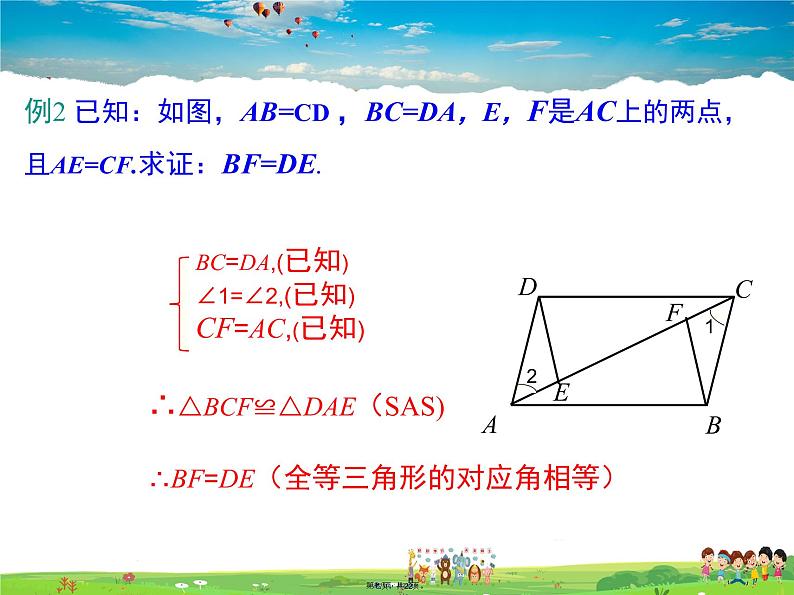
例2 已知：如图，AB=CD ，BC=DA，E，F是AC上的两点，且AE=CF.求证：BF=DE.
证明 在△ABC和△CDA中，
AB=CD,(已知)BC=DA,(已知)CA=AC,(公共边)
∴△ABC≌△CDA（SSS)
∴∠1=∠2（全等三角形的对应角相等）
在△ABC和△CDA中
BC=DA,(已知)∠1=∠2,(已知)CF=AC,(已知)
∴△BCF≌△DAE（SAS)
∴BF=DE（全等三角形的对应角相等）
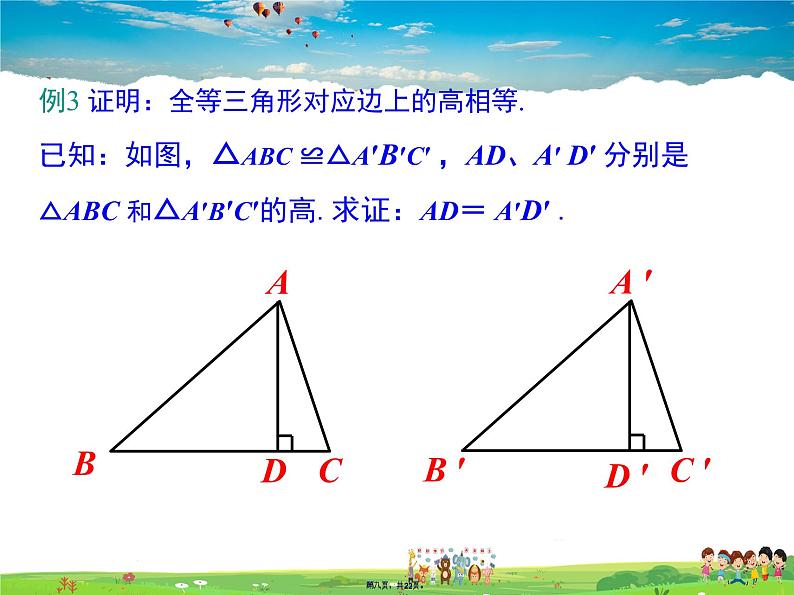
例3 证明：全等三角形对应边上的高相等.已知：如图，△ABC ≌△A′B′C′ ，AD、A′ D′ 分别是△ABC 和△A′B′C′的高.求证：AD＝ A′D′ .
解：因为△ABC ≌△A′B′C′ ，所以AB=A'B'（全等三角形对应边相等），∠ABD=∠A'B'D'（全等三角形对应角相等）.因为AD⊥BC，A'D'⊥B'C'，所以∠ADB=∠A'D'B'.在△ABD和△A'B'D'中，∠ADB=∠A'D'B'（已证），∠ABD=∠A'B'D'（已证），AB=AB（已证），所以△ABD≌△A'B'D'.所以AD=A'D'.
例4 如图，在四边形ABCD中，AB＝AD，BC＝DC，E为AC上的一动点(不与A重合)，在点E移动的过程中BE和DE是否相等？若相等，请写出证明过程；若不相等，请说明理由．
解：相等．理由如下：在△ABC和△ADC中，AB＝AD，AC＝AC，BC＝DC，∴△ABC≌△ADC(SSS)，∴∠DAE＝∠BAE.在△ADE和△ABE中，AB＝AD，∠DAE＝∠BAE，AE＝AE，∴△ADE≌△ABE(SAS)，∴BE＝DE.
本题考查了全等三角形的判定和性质，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．本题要特别注意“SSA”不能作为全等三角形一种证明方法使用．
例5 如图，已知CA=CB,AD=BD，M，N分别是CA，CB的中点，求证：DM=DN.
在△ABD与△CBD中
∴△ACD≌△BCD（SSS）
又∵M，N分别是CA，CB的中点，
在△AMD与△BND中
∴△AMD≌△BND（SAS）
1.如图，已知AC=DB，∠ACB=∠DBC，则有△ABC≌△ ，理由是 ， 且有∠ABC=∠ ，AB= ；
2.已知：如图，AB=AC,AD是△ABC的角平分线， 求证：BD=CD.
∵AD是△ABC的角平分线，
∴ ∠BAD=∠CAD，
在△ABD和△ACD中，
∴△ABD≌△ACD（SAS）.
已知：如图，AB=AC, BD=CD，求证： ∠ BAD= ∠ CAD.
∴△ABD≌△ACD（SSS）.
已知：如图，AB=AC, BD=CD，E为AD上一点，求证： BE=CE.
在△ABE和△ACE中，
∴△ABE≌△ACE（SAS）.
3. 如图，CD⊥AB于D点，BE⊥AC于E点，BE，CD交于O点，且AO平分∠BAC.求证：OB＝OC.
证明：∵BE⊥AC，CD⊥AB， ∴∠ADC＝∠BDC＝∠AEB＝∠CEB＝90°. ∵AO平分∠BAC， ∴∠1＝∠2.在△AOD和△AOE中，
∴△AOD≌△AOE(AAS).
在△BOD和△COE中，
∴△BOD≌△COE(ASA).
找夹角的另一边(SAS)
找夹角的另一角(ASA)
找除夹边外的任意一边(AAS)
第二十一页，共23页。
三角形全等的判定。2.经历探索三角形全等的几种判定方法的过程，能进行合情推理。3.培养良好的几何思维，体会几何学的应用价值．。(1)全等三角形对应角相等、对应边相等。以添加一边或一角都可以得到这两个三角形全等．若根据“SAS”判定时，则可以添加AC＝DC。若根据“ASA”判定时，则可以添加∠B＝∠E。若根据AAS判定时，则可以添加∠A＝∠D.。（1）已知一边一角，可任意添加一个角的条件，用AAS或ASA判定全等
第二十三页，共23页。
第二十一页，共22页。