高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式示范课课件ppt

这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式示范课课件ppt，共25页。PPT课件主要包含了新知初探·课前预习，实数x，答案A，答案D，题型探究·课堂解透，x0x1，答案ABD等内容，欢迎下载使用。

课程标准(1)掌握一元二次不等式的解法．(2)能根据“三个二次”之间的关系解决简单问题．
教 材 要 点要点一　一元二次不等式的概念一般地，我们把只含有______未知数，并且未知数的最高次数是____的不等式，称为一元二次不等式❶.一元二次不等式的一般形式是ax2＋bx＋c>0或ax2＋bx＋c<0，其中a，b，c均为常数，a≠0.要点二　二次函数的零点一般地，对于二次函数y＝ax2＋bx＋c，我们把使ax2＋bx＋c＝0的________叫做二次函数y＝ax2＋bx＋c的零点❷.
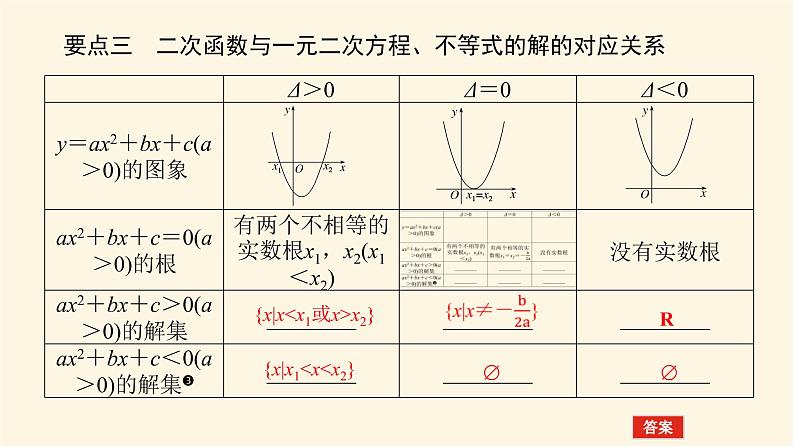
要点三　二次函数与一元二次方程、不等式的解的对应关系
{x|xx2}
{x|x1助 学 批 注批注❶　(1)“一元”指的是只有一个未知数，不代表只有一个字母，如a，b，c等．(2)“二次”指的是未知数的最高次必须存在并且是2，并且最高次系数不为0. 批注❷　零点不是点，是交点的横坐标，是数． 批注❸　对于一元二次不等式的二次项系数为正且存在两个根的情况下，其解集的常用口诀是：大于取两边，小于取中间．
基 础 自 测1.思考辨析(正确的画“√”，错误的画“×”)(1)mx2＋5x＜0是一元二次不等式．(　　)(2)若不等式ax2＋bx＋c＜0的解集为{x|x1＜x＜x2}，则必有a＞0.(　　)(3)若不等式ax2＋bx＋c＞0的解集是{x|x＜x1或x＞x2}，则方程ax2＋bx＋c＝0的两个根是x1和x2.(　　)(4)若方程ax2＋bx＋c＝0没有实数根，则不等式ax2＋bx＋c＞0的解集为R.(　　)
2．不等式(x＋1)(x－3)<0的解集是(　　)A．{x|－13}D. {x|x<－3或x>1}
解析：由(x＋1)(x－3)<0，解得－13．不等式x2－4>0的解集是(　　)A.{x|－22} D．{x|x<－2或x>2}
解析：x2－4＝(x＋2)(x－2)>0，解得x<－2或x>2，所以不等式的解集为{x|x<－2或x>2}．
4．不等式2x2－x≤0的解集为____________．
方法归纳解不含参数的一元二次不等式的一般步骤
巩固训练1　(1)不等式x2＋2x－3>0的解集是(　　)A．{x|x<－3或x>1} B．{x|x<－1或x>3}C．{x|－1解析：由x2＋2x－3>0，得(x－1)(x＋3)>0，解得x<－3或x>1.所以原不等式的解集为{x|x<－3或x>1}．
(2)不等式x(1－x)>0的解集是________． 
解析：∵不等式x(1－x)>0可化为x(x－1)<0，解得：0题型 2　三个“二次”之间的关系例2　已知关于x的不等式ax2＋bx＋c＞0的解集为{x|2＜x＜3}，求关于x的不等式cx2＋bx＋a＜0的解集． 
方法归纳已知以a，b，c为参数的不等式(如ax2＋bx＋c>0)的解集，求解其他不等式解集的一般步骤
题型 3　解含参数的一元二次不等式角度1　对判别式“Δ”进行讨论例3　解关于x的不等式2x2＋ax＋2＞0. 
角度2　对根的大小进行讨论例4　解关于x的不等式x2＋2x＋1－a2≤0(a∈R)．
解析：原不等式等价于(x＋1＋a)(x＋1－a)≤0.(1)当－1－a＜－1＋a，即a＞0时，－1－a≤x≤－1＋a；(2)当－1－a＝－1＋a，即a＝0时，不等式即(x＋1)2≤0，∴x＝－1；(3)当－1－a＞－1＋a，即a＜0时，－1＋a≤x≤－1－a.综上，当a＞0时，原不等式的解集为{x|－1－a≤x≤－1＋a}；当a＝0时，原不等式的解集为{x|x＝－1}；当a＜0时，原不等式的解集为{x|－1＋a≤x≤－1－a}．
角度3　对二次项系数进行讨论例5　设a∈R，解关于x的不等式ax2＋(1－2a)x－2＞0. 
方法归纳解含参数的一元二次不等式的步骤
巩固训练3　[2022·河北唐山高一期末]已知关于x的不等式：ax2－(3a＋1)x＋3<0.(1)当a＝－2时，解此不等式；(2)当a>0时，解此不等式．