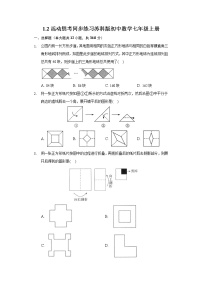
初中数学苏科版七年级上册1.2 活动 思考精练

随堂测试

1.2活动 思考

一．选择题(每小题2分  共32分)

1．将一个长方形框架拉成一个平行四边形后，长方形与平行四边形相比(　　)

A．周长相等，面积相等           B．周长相等，面积不等

C．周长不等，面积不等           D．周长不等，面积相等

2．要从一张长为40 cm，宽为20 cm的长方形纸片中，剪出长为18 cm，宽为12 cm的长方形纸片，最多能剪出(　　)

A．1张              B．2张              C．3张               D．4张

3．把一张长方形纸片按如图1－2－1①，②的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是(　　)

4.小说《达·芬奇密码》中的一个故事里出现了一串神秘排列的数，将这串令人费解的数按从小到大的顺序排列为1，1，2，3，5，8，…，则这列数的第8个数是(　　)

A．13             B．21                C．34                D．55

5.小亮玩数弹珠游戏，他发现：若放1个弹珠在桌子上，有1种数法；放2个弹珠在桌子上，有1，1；2，共2种不同的数法；放3个弹珠在桌子上，有1，1，1；1，2；2，1；3，共4种不同的数法，…，按照此规律，放5个弹珠在桌子上，不同的数法共有(　　)

A．8种           B．12种             C．16种              D．20种

6.从1开始得到如下的一列数：1，2，4，8，16，22，24，28，…，其中每一个数加上自己的个位数，成为下一个数，上述一列数中，小于100的数的个数为(　　)

A．21             B．22               C．23                D．99

7．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值为(　　)

A．180             B．182            C．184               D．186

8．下面 A,B,C,D四幅图中哪幅图是由图1平移得到的?(      )

                  A              B             C               D

9．用一种如下形状的地砖,不能把地面铺成既无缝隙又不重叠的是(   )｡

A.正三角形       B.正方形     C.长方形     D.正五边形

10．如图所示,甲、乙是两张画有图形的透明胶片,把其中一张向右平移到另一张上,形成的图形是(  ).

11.已知:,,,,…,若符合前面式子的规律,则的值为(  ) 

A.179               B.140               C.109             D.210

12 ．下列一组是按一定规律排列的数:1,2,4,8,16,……,则第2021个数是(    )

A、22020         B、22021      C、22022       D、22021-1

13.四个电子宠物排座位,一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、4号座位上(如图所示),以后它们不停地变换位置,第一次上下两排交换,第二次是在第一次换位后,再左右两列交换位置,第三次上下两排交换,第四次再左右两列交换……这样一直下去,则第2021次交换位置后,小兔子坐在(    )号位上｡ 

A.1                 B.2                 C.3                 D.4

          第13题图                                  第14题图

14.如图所示图形中,是由一个矩形沿顺时针方向旋转90°后所形成的图形的是(  )

A.(1)(4)           B.(2)(3)           C.(1)(2)              D.(2)(4)

15．已知下列一组数:;用代数式表示第个数,则第个数是(   )

A、;         B、;         C、 ;           D、

16．如图，一串按一定规律排列的珠子，珠子的颜色有黑色和白色两种，这串珠子有一部分被一个长方体的盒子遮住了，则这串珠子被盒子遮住的部分有（ ）颗．

A．6             B．3             C．29             D．27

二．填空题(每小题2分  共24分)

17．如图所示的方式搭正方形：搭n个正方形需要小棒　  　根．

18．要把一个正方体分割成8个小正方体，至少需要切3刀，因为这8个小正方体都只有三个面是现成的，其他三个面必须用刀切3次才能切出来，那么，要把一个正方体分割成27个小正方体，至少需要切_______刀，分割成64个小正方体，至少需要切______刀．

19．小明同学在上楼梯时发现：当只有一个台阶时，有一种走法；当有两个台阶时，可以一阶一阶地上，或者一步上两个台阶，共有两种走法；如果他一步只能上一个或者两个台阶，根据上述规律，当有三个台阶时，他有三种走法，那么当有四个台阶时，共有______种走法．

20．用同样大小的黑色棋子按如图1－2－3所示的规律摆放：则第⑦个图案中有_______个黑色棋子

           第20题图                               第21题图

21．下列图案是用长度相同的火柴棒按一定的规律拼搭而成的，图案①需8根火柴棒，图案②需15根火柴棒，…，按此规律，图案⑦需________根火柴棒．

22.下列图形是由一些小正方形和实心圆按一定规律排列而成的，如图1－2－6所示，按此规律排列下去，第⑳个图形中有______个实心圆．

第22题图                                     第23题图

23.如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是______,第个“广”字中的棋子个数是___ _____

24．已知123456789101112…997998999是由连续整数1至999排列组成的一个数，在该数中从左往右数第2021位上的数字为________．

25．1766年德国人提丢斯发现,太阳系中的行星到太阳的距离遵循下表所示的规律:根据表格,第7颗行星到太阳的距离是____天文单位.

26.观察下面两行数:

2，  4，  8，  16，  32，  64，  …　　　①

5，  7， 11， 19，  35，   67，  …      ②

根据你发现的规律,取每行数的第10个数,求得它们的和是(要求写出最后的计算结果)_____.

27．下列给出的一串数:2,5,10,17,26,?,50.仔细观察后回答:缺少的数?是__________.

28．邓老师设计了一个计算程序,输入和输出的数据如下表:那么,当输入数据是时,输出的数据是_____.

三．解答题(共44分)

29．（6分）观察下面一列数,探求其规律:

(1)请问第7个,第8个,第9个数分别是什么?

(2) 第2021个数是什么?如果这列数无限排列下去,越来越接近哪一个数?

30（8分）①计算并观察下列三组算式并填空：；；

②已知25×25＝625，则24×26＝     （不要计算）

③你能举出一个类似的例子吗？

④更一般地，若a×a＝m，则(a＋1)(a－1)＝      .

31．（6分）用火柴棒按如图所示方式搭图形，按照这种方式搭下去，（1）求搭第2020个图形需火柴棒的根数；（2）求第n个图形需火柴棒的根数．

32（9分）下图是2020年8月份的月历，由图回答下列问题：

（1）十字框框出的5个数与十字框中间的数有什么关系？

（2）如果十字框框出的5个数的和为55，那么十字框中间的数是多少？

（3）十字框框出的5个数的和可以是110吗？

33.（6分）某餐厅中，一张桌子可坐6人，有以下两种摆放方式：（1）当有n张桌子时，两种摆放方式各能坐多少人？（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌为什么？

34.（9分）观察下列等式：第1个等式：a1＝＝×（1﹣）第2个等式：a2＝＝×（﹣）第3个等式：a3＝＝×（﹣）第4个等式：a4＝＝×（﹣）…请解答下列问题：

（1）按以上规律列出第5个等式：a5＝　   　；

（2）用含有n的代数式表示第n个等式：an＝　   　（n为正整数）：

（3）求a1+a2+a3+a4+……+a100的值；

（4）探究计算：+++…+

参考答案

一．选择题(每小题2分  共32分)

1． B

2． C

3． C

4.  B

5.　C　

6.　A　

7．C　

8．  D 

9． D 

10． A

11. C

12 ． A  

13.  A 

14. B

15． B 

16． D

二．填空题(每小题2分  共24分)

17． (3n+1)  　

18． 6_ ___9___

19． ___5____

20． ___19_____

21． __50__

22. ____42____

23. _2n5_

24． ___1__

25． ____10_____

26._2051__.

27． ____.

三．解答题(共44分)

29． (1)第7、8、9个数分别为

(2) -,如果这列数无限排列下去,越来越接近0.

30（8分）

解：① 根据题意，有12×12=144，11×13=143；

② 由①分析可得，24×26=25×25-1，又由25×25=625，则24×26=624；

③ 根据①②的结论，举例如下20×20=400，则19×21=399；

④ 若a×a=m，则（a+1）（a-1）=a×a-1=m-1．

31．

（1）根据题意分析可得：第一个图形用了12根火柴；即12＝6（1+1）；

第二个图形用了18根火柴；即18＝6（2+1）；第三个图形用了24根火柴；即18＝6（3+1）；……按照这种方式搭下去，搭第2020个图形需6（n+1）根火柴．

6×（2020+1）＝12126，故答案为12126；（2）第n个图形需6（n+1）根火柴

32（9分）

（1）十字框框出的5个数中，上、下、左、右的4个数分别比中间的数小7、大7、小1、大1，这5个数的和是中间的数的5倍；

（2）因为十字框框出的5个数的和是中间数的5倍，55÷5＝11，所以十字框中间的数是11；

（3）如果十字框框出的数是110，由于这5个数的和是中间数的5倍，110÷5＝22，那么中间数应该是22，由图可以发现，22的右边没有数了，所以这5个数的和不可能是110.

33.

(1)第一种中，只有一张桌子是6人，后边多一张桌子多4人。即有n张桌子时是6+4（n-1）=4n+2第二种中，有一张桌子是6人，后边多一张桌子多2人，即6+2(n-1)=2n+4故答案为：第一种能坐4n+2人，第二种能坐2n+4人。分别求出两种对应的n的值，或分别求出n=25时，两种不同的摆放方式对应的人数，即可作出判断。打算用第一种摆放方式来摆放餐桌。因为，当n=25时，4×25+2=102＞98当n=25时，2×25+4=54＜98所以，选用第一种摆放方式。故答案为选择第一种

34.

（1）∵第1个等式：a1＝＝×（1﹣）第2个等式：a2＝＝×（﹣）第3个等式：a3＝＝×（﹣）第4个等式：a4＝＝×（﹣）…

∴第5个等式：a5＝（），故答案为：×（）；

（2）由题意可得，第n个等式：an＝＝×（），故答案为：（）；

（3）a1+a2+a3+a4+……+a100＝×（1﹣）+×（﹣）+×（﹣）+×（﹣）+…+×（）＝×（1﹣++…+）＝×（1﹣）＝＝；

（4）+++…+＝×（1﹣+…+）＝×（1﹣）＝＝．