






初中数学人教版九年级上册22.3 实际问题与二次函数示范课课件ppt
展开1.二次函数y=2x2-8x+9的对称轴是 ,顶点坐标是 .当x= 时,函数有最_____ 值,是 .
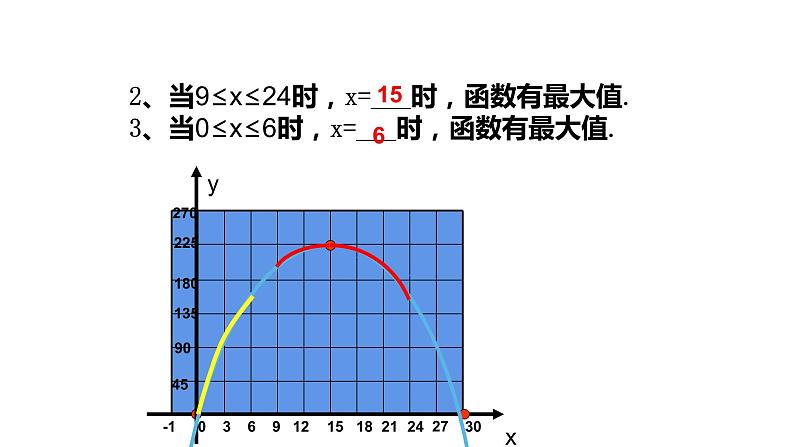
2、当9≤x≤24时,x=___时,函数有最大值.3、当0≤x≤6时,x=___时,函数有最大值.
例1 小孟有总长为60m的篱笆,想围成一个矩形羊圈,这个羊圈的长、宽各为多少时,羊圈的面积最大?
变式1 小孟有总长为60m的篱笆,想围成一个一边靠墙的矩形羊圈,墙长32m,这个羊圈的长、宽各为多少时,羊圈的面积最大,最大面积是多少?
变式2 小孟有总长为60m的篱笆,想围成一个一边靠墙的矩形羊圈,墙长18m,这个羊圈的长、宽各为多少时,羊圈的面积最大,最大面积是多少?
解:设羊圈面积为Sm2,与墙垂直的一边为x米,则与墙垂直的一边为(60-2x)米
二次函数解决几何面积最值问题的方法
1、设,设未知数2、列出函数解析式,配方变形3、自变量的取值范围4、最值,必须在自变量的取值范围内求得最大值.5、答
问题1.已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如果调整价格 ,每涨价1元,每星期要少卖出10件。怎样定价才能让每星期利润达到6090元?
分析:没调价之前商场一周的利润为 元;设销售单价上调了x元,那么每件商品的利润可表示为 元,每周的销售量可表示为 件,一周的利润可表示为 元,要想获得6090元利润可列方程 。
(20+x)( 300-10x)
(20+x)( 300-10x) =6090
问题2.已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格,每涨价一元,每星期要少卖出10件。该商品应定价为多少元时,商场能获得最大利润?
y=(60+x-40)(300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250
因为x=-10<0,开口向下y有最大值所以x=5时,y最大=6250元
方法1:设每件涨价x元,利润为y元.
答:当定价为65元时,获得最大利润为6250元。
方法2:设每件售价x元,利润为y元。
自变量的取值范围 60≤x≤90
300-10(x-60)
y=(x-40)[300-10(x-60)]
问题3.已知某商品的进价为每件40元。现在的售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格,每降价一元,每星期可多卖出20件。如何定价才能使利润最大?
方法1 解:设降价x元时,利润为y元。
y=(60-x-40)(300+20x) (0≤x≤20)
方法2 解:设定价为x元时,利润为y元。
y=(x-40)[300+20(60-x)] (40≤x≤60)
(1)审题,列出二次函数的解析式.(2)并根据自变量的实际意义,确定自变量的取值范围;(3)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值。
(某超市经销一种销售成本为每件40元的商品.据市场调查分析,如果按每件50元销售,一周能售出500件;若销售单价每涨1元,每周销量就减少10件.设销售单价为x元(x≥50),一周的销售量为y件.
(1)写出y与x的函数关系式(标明x的取值范围)
(2)设一周的销售利润为S,写出S与x的函数关系式,并确定当单价在什么范围内变化时,利润随着单价的增大而增大?
(3)在超市对该种商品投入不超过10000元的情况下,使得一周销售利润达到8000元,销售单价应定为多少?
实际问题与二次函数PPT课件免费下载: 人教版初中数学九年级上册课文《实际问题与二次函数》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。
初中人教版22.3 实际问题与二次函数集体备课ppt课件: 这是一份初中人教版22.3 实际问题与二次函数集体备课ppt课件,共14页。PPT课件主要包含了来到商场,我来当老板,牛刀小试,创新学习,解这类题目的一般步骤等内容,欢迎下载使用。
初中数学人教版九年级上册22.3 实际问题与二次函数图片课件ppt: 这是一份初中数学人教版九年级上册22.3 实际问题与二次函数图片课件ppt,共9页。PPT课件主要包含了预习导学,自学指导,探究1等内容,欢迎下载使用。













