





人教版九年级上册22.1.1 二次函数优质课ppt课件
展开人教版初中数学九年级上册
22.1.7 二次函数字母系数与图象的关系 教学设计
一、教学目标:
1.理解并掌握二次函数字母系数与图象的关系.(难点)
2.能灵活利用二次函数字母系数与图象的关系解决相关问题.(重点)
二、教学过程:
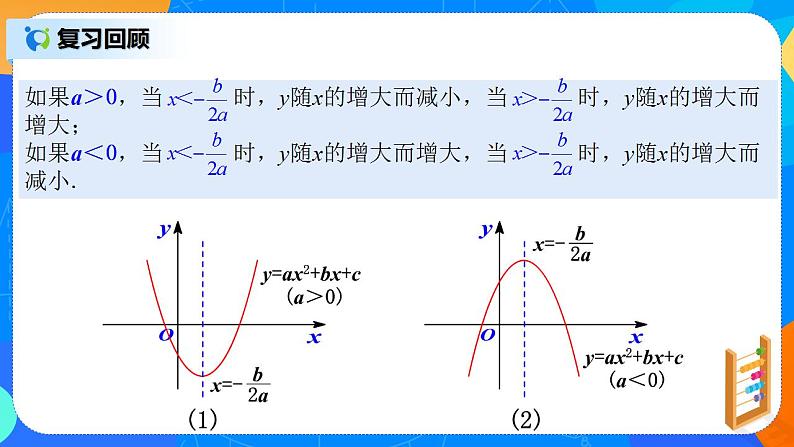
复习回顾
(1)对称轴是直线_______,顶点是_________.
(2)如果a>0时,那么当_______时,y最小值=________;
(3)如果a<0时,那么当_______时,y最大值=________.
(4)如果a>0,当________时,y随x的增大而减小,当_______时,y随x的增大而增大;
(5)如果a<0,当________时,y随x的增大而增大,当________时,y随x的增大而减小.
知识精讲
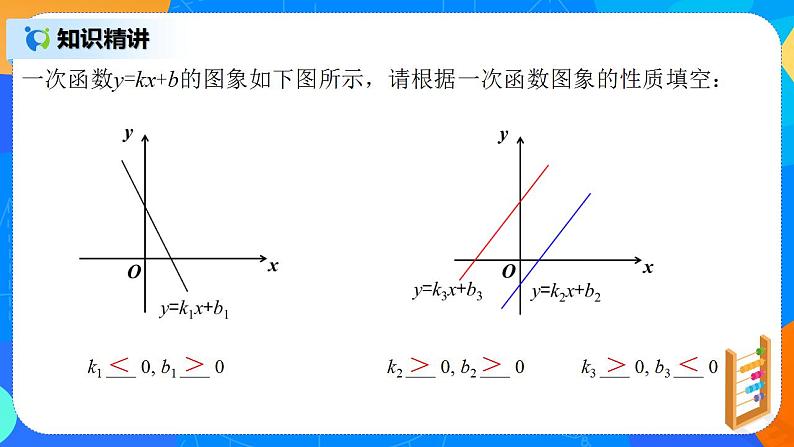
一次函数y=kx+b的图象如下图所示,请根据一次函数图象的性质填空:
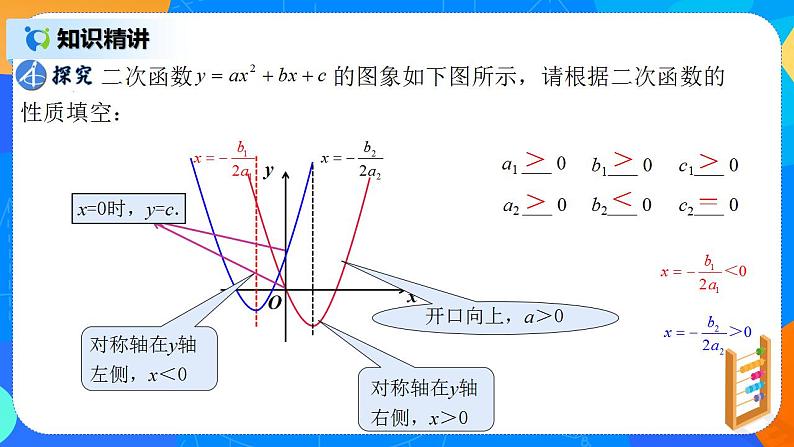
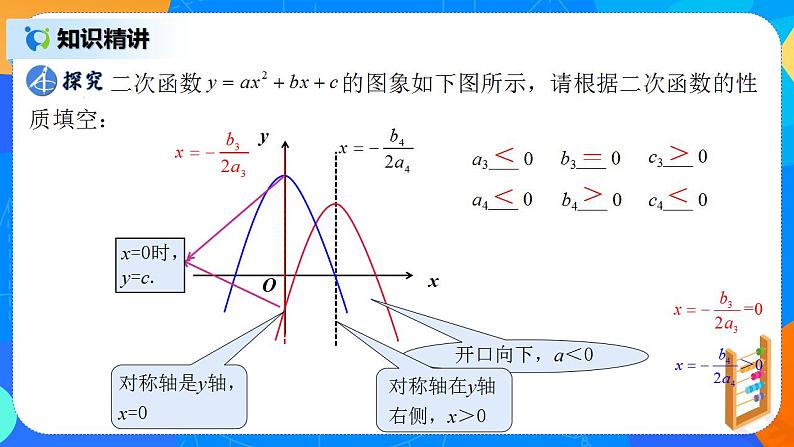
探究:二次函数的图象如下图所示,请根据二次函数的性质填空:
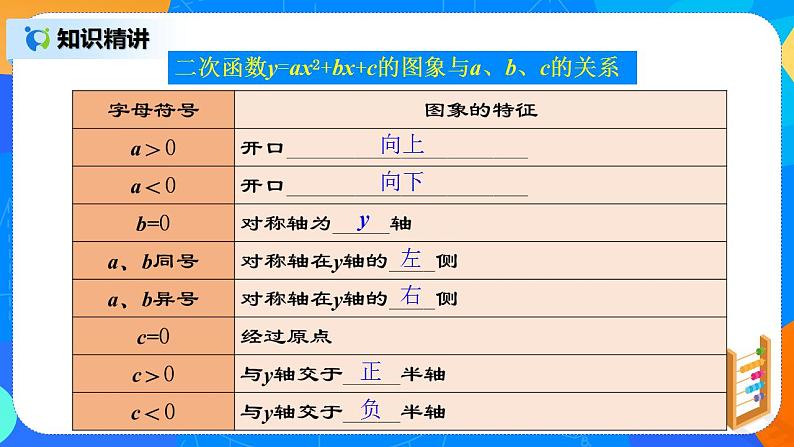
二次函数y=ax2+bx+c的图象与a、b、c的关系
典例解析
例1.在同一坐标系中一次函数y=ax-b和二次函数y=ax2+bx+c的图象可能为( )
【分析】解:A.由抛物线可知,a>0,x=−b/2a>0,得b<0,由直线可知,a>0,b>0,故本选项错误;
B.由抛物线可知,a>0,由直线可知,a<0,故本选项错误;
C.由抛物线可知,a<0,x=−b/2a>0,得b>0,由直线可知,a<0,b>0,故本选项正确;
D.由抛物线可知,a<0,由直线可知,a>0,故本选项错误.
故选:C.
【针对练习】在同一平面直角坐标系中,函数y=ax2+bx(a≠0)与y=ax+b的图象可能是( )
例2.如图,一次函数y1=x与二次函数y2=x2+bx+c的图像相交于P、Q两点,则函数y=x2+(b-1)x+c的图像可能是( )
解: 由=x2+bx+c图象可知,对称轴x=>0,,
,抛物线与y轴的交点在x轴下方,故选项B,C错误,
抛物线的对称轴为,
∴,
∴抛物线y=x2+(b-1)x+c的对称轴在y轴的右侧,故选项D错误,
故选:A.
例3.二次函数(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:
x | … | 0 | 1 | 2 | … | ||
… | t | m | n | … |
且当时,其对应的函数值.有下列结论:
①;②和3是关于x的方程的两个根;③对称轴为;④;其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
解:二次函数(a,b,c是常数,),
当时,,
当时,,
.
当时,其对应的函数值,
二次函数开口向下,.
,,,
.(①结论符合题意)
时,,
是关于x的方程的根.
对称轴,,(③结论不符合题意)
和3是关于x的方程的两个根.(②结论符合题意)
时,,
时,,
.
.(④结论不符合题意)
正确的结论有2个.
故选:C.
【针对练习】已知二次函数(,,是常数,且)的自变量与函数值的部分对应值如下表:
… | 0 | 1 | 2 | … | ||
… | … |
当时,与其对应的函数值,给出下列四个结论:①;②关于的方程的两个根是和2;③;④(为任意实数.)其中正确结论的个数是( )
A.1 B.2 C.3 D.4
解:由表格可知,该抛物线图象经过点,
∴ 该抛物线的对称轴为,;
∵ 当时,与其对应的函数值,
∴ 抛物线开口向上,
∴ ,
∴ ,故①正确;
由图象经过的点和抛物线对称性可知,,故②正确;
由当时,与其对应的函数值,
得到
∴ ,
当时,,
∴ ,故③错误;
由对称轴为,图象开口向上可得:
,
∴ ,故④正确;
故选:C.
例4.如图,抛物线过点,且对称轴为直线,有下列结论①;②:③抛物线经过点与点,则;④无论a,b,c取何值,抛物线都经过同一个点;⑤,其中正确的结论是( )
A.①②③ B.③④⑤ C.②③④ D.②④⑤
解:由图象可知,抛物线开口向上,则a>0,
∵ 对称轴为直线x=1,
∴ ﹣=1,
∴ b=﹣2a<0,
∴ b<0,
∵ 抛物线与y轴交于负半轴,
∴ c<0,
∴ abc>0,故①错误;
∵ 抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,
∴ 抛物线y=ax2+bx+c过点(3,0),
∴ 当x=3时,y=9a+3b+c=0,
∵ a>0,
∴ 10a+3b+c>0,故②正确;
∵ 对称轴为x=1,且开口向上,
∴ 离对称轴水平距离越大,函数值越大,
∵|4-1|<|﹣3-1|,
∴ y1<y2,故③错误;
当x=﹣时,,
∵ 当x=﹣1时,y=a﹣b+c=0,
∴ 当x=﹣时,y=a•(﹣)2+b•(﹣)+c=0,
即无论a,b,c取何值,抛物线都经过同一个点(﹣,0),故④正确;
x=m对应的函数值为y=am2+bm+c,
x=1对应的函数值为y=a+b+c,
又∵x=1时函数取得最小值,
∴ am2+bm+c≥a+b+c,即am2+bm≥a+b,
∵ b=﹣2a,
∴ a+b=﹣a,
∴ am2+bm≥﹣a,
∴ am2+bm+a≥0,故⑤正确;
故选:D.
【针对练习】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论:①abc>0;②2a+b<0;③a﹣b+c>0;④9a+3b+c<0,其中正确的是( )
A.①③④ B.①②③ C.①③ D.②③
解:由抛物线的开口向上,得到a>0,
∵ ﹣>0,
∴ b<0,
由抛物线与y轴交于负半轴,得到c<0,
∴ abc>0,选项①正确;
∵ 对称轴为直线x=1,
∴ ﹣=1,即b=﹣2a,
∴ 2a+b=0,选项②错误;
根据图象知,当x=﹣1时,y>0,
即a﹣b+c>0.选项③正确;
∵ 抛物线对称轴为直线x=1,
∴ x=3与x=﹣1时函数值相等,
又∵ x=﹣1时,y>0,
∴ x=3时,y=9a+3b+c>0,选项④错误;
则其中正确的选项有①③.
故选:C.
例5.如图,二次函数的图象关于直线对称,与x轴交于,两点,若,则下列四个结论:①,②,③,④.
正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
解:∵对称轴为直线x=1,-2<x1<-1,
∴3<x2<4,①正确,
∵ = 1,
∴b=- 2а,
∴3a+2b= 3a-4a= -a,
∵a>0,
∴3a+2b<0,②错误;
∵抛物线与x轴有两个交点,
∴b2 - 4ac > 0,根据题意可知x=-1时,y<0,
∴a-b+c<0,
∴a+c<b,
∵a>0,
∴b=-2a<0,
∴a+c<0,
∴b2 -4ac > a+ c,
∴b2>a+c+4ac,③正确;
∵抛物线开口向上,与y轴的交点在x轴下方,
∴a>0,c<0,
∴a>c,
∵a-b+c<0,b=-2a,
∴3a+c<0,
∴c<-3a,
∴b=–2a,
∴b>c,以④错误;
故选B
例6.如图,已知抛物线的顶点是,与x轴交于点,给出以下结论:①;②;③若,则或;④.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
解:∵抛物线开口向上,
∴,
∵对称轴为直线,
∴,
∵抛物线与y轴的交点在负半轴,
∴,
∴,故①错误;
∵抛物线与x轴交于,对称轴为,
∴抛物线与x轴的另一个交点为,
当x=2时,位于x轴上方,
∴,故②正确;
根据抛物线的对称轴为直线x=-1可知,当y=c时,x=-2或0,
根据二次函数图象,若,则或,故③正确;
当时,①,
当时,②,
+②得:,即,
∵对称轴为直线,
∴,
∴,
∴,
得:,解得,
∴,
即,故④正确;
综上分析可知,正确的有3个,故C正确.
故选:C.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
达标检测
1.已知二次函数?=??2+??−?(?≠0),其中?>0、?>0,则该函数的图象可能为( )
2.已知,在同一平面直角坐标系中,二次函数?=??2与一次函数?=??+?的图象如图所示,则二次函数?=??2+??+?的图象可能是( )
3.已知二次函数?=??2+??+?(?≠0)的图象如图所示,有下列结论:①???>0;②4?+2?+?>0;③?−?>?;④3?>−?;⑤?+?>?(??+?)(?≠1,m为实数),其中正确的结论有( )个.
A.2个 B.3个 C.4个 D.5个
4.已知抛物线y=ax2+bx+c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc>0;②2c﹣3b <0;③5a +b+2c=0;④若B(4/3,y1)、C(1/3,y2)、D(−1/3,y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )
A.1 B.2 C.3 D.4
5.如图所示,已知二次函数?=??2+??+?的图象与?轴交于?,?两点,与?轴交于点?,对称轴为直线?=1,直线?=−?+?与抛物线?=??2+??+?交于?,?两点,?点在?轴下方且横坐标小于3,则下列结论:①a-b+c<0;②2?+?+?>0;③?(??+?)≤?+?;④a>-1,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
初中数学浙教版九年级上册1.1 二次函数获奖课件ppt: 这是一份初中数学浙教版九年级上册1.1 二次函数获奖课件ppt,共19页。PPT课件主要包含了学习目标,复习回顾,x0时yc,知识精讲,典例解析,x-1,针对练习,①②⑤,达标检测,直线x1等内容,欢迎下载使用。
初中数学人教版九年级上册22.3 实际问题与二次函数习题课件ppt: 这是一份初中数学人教版九年级上册22.3 实际问题与二次函数习题课件ppt,共19页。
九年级上册1.1 二次函数完美版教学课件ppt: 这是一份九年级上册1.1 二次函数完美版教学课件ppt,共17页。PPT课件主要包含了学习目标,复习回顾,x0时yc,知识精讲,典例解析,x-1,针对练习,①②⑤,达标检测,直线x1等内容,欢迎下载使用。














