

人教版九年级上册第二十四章 圆综合与测试综合训练题
展开第24章 圆 选择题
1.(2022·广东汕尾·九年级期末)已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
2.(2022·广东肇庆·九年级期末)如图所示,△ABC是⊙O的内接三角形.若∠ABC=70°,则∠AOC的度数等于( )
A.140° B.130° C.120° D.110°
3.(2022·广东东莞·九年级期末)P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为( )
A.5 B.6 C.8 D.10
4.(2022·广东广州·九年级期末)正十边形的中心角是( )
A.18° B.36° C.72° D.144°
5.(2022·广东广州·九年级期末)平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )
A.圆内 B.圆上 C.圆外 D.圆上或圆外
6.(2022·广东·湖景中学九年级期末)若⊙O的半径为6cm,PO=8cm,则点P的位置是( )
A.在⊙O外 B.在⊙O上 C.在⊙O内 D.不能确定
7.(2022·广东·铁一中学九年级期末)已知⊙O的半径为6,A为线段PO的中点,当OP=12时,点A与⊙O的位置关系为( )
A.点A在⊙O上 B.点A在⊙O外
C.点A在⊙O内 D.点A与⊙O位置不确定
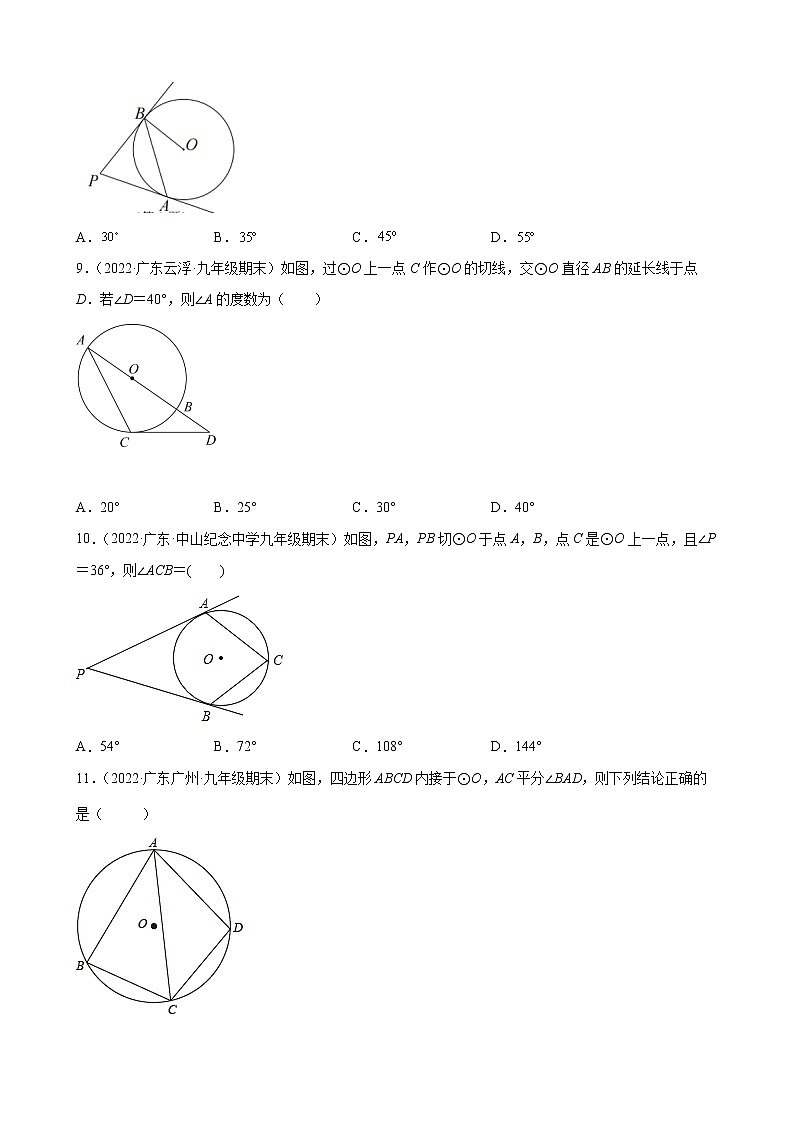
8.(2022·广东深圳·九年级期末)如图,PA,PB是⊙O的切线,A,B是切点,若,则( )
A. B. C. D.
9.(2022·广东云浮·九年级期末)如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
A.20° B.25° C.30° D.40°
10.(2022·广东·中山纪念中学九年级期末)如图,PA,PB切⊙O于点A,B,点C是⊙O上一点,且∠P=36°,则∠ACB=( )
A.54° B.72° C.108° D.144°
11.(2022·广东广州·九年级期末)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
12.(2022·广东阳江·九年级期末)如图,AB是⊙O的直径,AC,BC是⊙O的弦,若,则的度数为( )
A.70° B.90° C.40° D.60°
13.(2022·广东东莞·九年级期末)如图,△ABC的顶点A、B、C、均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
A.30° B.45° C.60° D.70°
14.(2022·广东·铁一中学九年级期末)如图,⊙O的直径CD垂直弦AB于点E,且CE=4,OB=8,则AB的长为( )
A.4 B.4 C.6 D.8
15.(2022·广东中山·九年级期末)如图,D是等边△ABC外接圆上的点,且∠CAD=20°,则∠ACD的度数为( )
A.20° B.30° C.40° D.45°
16.(2022·广东广州·九年级期末)如图的直径垂直于弦,垂足是,,,的长为( )
A. B. C. D.
17.(2022·广东北江实验学校九年级期末)如图,四边形ADBC内接于⊙O,∠AOB=122°,则∠ACB等于( )
A.131° B.119° C.122° D.58°
18.(2022·广东江门·九年级期末)如图,△ABC的外接圆半径为8,∠ACB=60°,则AB的长为( )
A.8 B.4 C.6 D.4
19.(2022·广东潮州·九年级期末)如图,正五边形ABCDE边长为6,以A为圆心,AB为半径画圆,图中阴影部分的面积为( ).
A. B. C. D.
20.(2022·广东广州·九年级期末)如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A. B. C.3 D.5
21.(2022·广东广州·九年级期末)在平面直角坐标系xOy中,已知点A(﹣4,﹣3),以点A为圆心,4为半径画⊙A,则坐标原点O与⊙A的位置关系是( )
A.点O在⊙A内 B.点O在⊙A外
C.点O在⊙A上 D.以上都有可能
22.(2022·广东惠州·九年级期末)如图,已知圆心角的度数为,则圆周角的度数是( )
A. B. C. D.
23.(2022·广东茂名·九年级期末)如图,点A、B、C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
24.(2022·广东韶关·九年级期末)如图,AB是⊙的直径,AC是⊙的切线,A为切点,BC与⊙交于点D,连结OD.若,则∠AOD的度数为( )
A. B. C. D.
25.(2022·广东深圳·九年级期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心为圆心的圆,如图2,已知圆心在水面上方,且被水面截得的弦长为6米,半径长为4米.若点为运行轨道的最低点,则点到弦所在直线的距离是( )
A.1米 B.米 C.2米 D.米
26.(2022·广东韶关·九年级期末)如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A.4 B.6.25 C.7.5 D.9
27.(2022·广东珠海·九年级期末)如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A.20° B.30° C.40° D.50°
28.(2022·广东·东莞市东城中学九年级期末)如图,正六边形ABCDEF内接于,过点O作弦BC于点M,若的半径为4,则弦心距OM的长为( )
A. B. C.2 D.
29.(2022·广东·台山市教师发展中心九年级期末)圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
30.(2022·广东·台山市教师发展中心九年级期末)“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为的直径,弦,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
A.12寸 B.13寸 C.24寸 D.26寸
31.(2022·广东阳江·九年级期末)如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A. B.3 C.2 D.4
32.(2022·广东·铁一中学九年级期末)如图,F为正方形ABCD的边CD上一动点,AB=2.连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为( )
A. B. C.3﹣ D.3+
33.(2022·广东·湖景中学九年级期末)如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是( )
A.30° B.45° C.60° D.40°
34.(2022·广东中山·九年级期末)如图所示,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
35.(2022·广东·东莞市东城中学九年级期末)如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径,扇形圆心解,则该圆锥母线长为( )
A.10 B. C.6 D.8
36.(2022·广东·东莞市光明中学九年级期末)如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=35°,则∠BDC=( )
A.85° B.75° C.70° D.55°
37.(2022·广东湛江·九年级期末)如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
38.(2022·广东韶关·九年级期末)已如⊙O的半径等于3,圈心O到直线l的距离为5,那么直线l与⊙O的位置关系是 ( )
A.直线l与⊙O相交 B.直线l与⊙O相离 C.直线l与⊙O相切 D.无法确定
39.(2022·广东湛江·九年级期末)如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是AB的中点,如果点C在圆上运动一周,那么点D运动过的路程长为( )
A. B. C.π D.2π
40.(2022·广东韶关·九年级期末)正六边形的周长为6,则它的面积为( )
A. B. C. D.
41.(2022·广东·中山纪念中学九年级期末)如图,直径AB为3的半圆,绕A点逆时针旋转60°,此时点B到了点B′处,则图中阴影部分的面积是( )
A.3π B. C.6π D.24π
42.(2022·广东广州·九年级期末)半径等于的圆中,垂直平分半径的弦长为( )
A. B. C. D.
43.(2022·广东中山·九年级期末)如图,在半径为的圆形纸片中,剪一个圆心角为90º的最大扇形(阴影部分),则这个扇形的面积为 ( )
A.π B. C.2π D.
44.(2022·广东·东莞市光明中学九年级期末)如图,在⊙O的内接正六边形ABCDEF中,AB=,则图中阴影部分的面积为( )
A. B. C. D.
45.(2022·广东汕头·九年级期末)如图,AB是⊙O的直径,AP是⊙O的切线,PB交⊙O于点C,点D在⊙O 上,若∠ADC=40°,则∠P的度数是( )
A.35° B.40° C.45° D.50°
46.(2022·广东潮州·九年级期末)如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A.3 B.1+ C.1+3 D.1+
47.(2022·广东广州·九年级期末)如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结, 则长的最大值为 ( )
A.3 B. C.4 D.
48.(2022·广东中山·九年级期末)如图,抛物线与轴交于、两点,是以点(0,3)为圆心,2为半径的圆上的动点,是线段的中点,连结.则线段的最大值是( )
A. B. C. D.
参考答案:
1.B
【解析】
⊙O最长的弦就是直径从而不难求得半径的长.
解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
2.A
【解析】
欲求∠AOC,又已知一圆周角,可利用圆周角与圆心角的关系求解.
因为∠ABC和∠AOC是同一条弧AC所对的圆周角和圆心角,所以∠AOC=2∠ABC×70°=140°.
本题考查圆周角定理,解题的关键是熟练掌握圆周角定理.
3.C
【解析】
根据勾股定理和垂径定理即可求得.
解:在过点P的所有⊙O的弦中,
如图,当弦与OP垂直时,弦最短,
此时,
得其半弦长为4,则弦长是8,
故选:C.
此题首先要能够正确分析出其最短的弦,然后综合运用垂径定理和勾股定理进行计算.
4.B
【解析】
正多边形的每个中心角相等,且其和是360°,故一个中心角的度数为360°除以正多边形的边数.
正十边形的每个中心角相等,且其和是360°,故一个中心角的度数为:360°÷10=36°
故选:B
本题考查了求正多边形中心角,这时要清楚正多边形的中心角都相等且它们的和组成一个周角.
5.A
【解析】
根据点到圆心的距离小于半径即可判断点P在⊙O的内部.
⊙O的半径为5,PO=4,
点P在⊙O的内部
故选A
本题考查了点与圆的位置关系,理解点与圆的位置关系是解题的关键.
6.A
【解析】
根据点到圆心的距离和圆的半径之间的数量关系,即可判断点和圆的位置关系.点到圆心的距离小于圆的半径,则点在圆内;点到圆心的距离等于圆的半径,则点在圆上;点到圆心的距离大于圆的半径,则点在圆外.
解:根据点到圆心的距离8cm大于圆的半径6cm,则该点在圆外.
故选A.
本题考查了点和圆的位置关系与数量之间的联系:当点到圆心的距离大于圆的半径时,则点在圆外.
7.A
【解析】
利用OP=12,A为线段PO的中点,则OA=6,因而点A与⊙O的位置关系为:点在圆上.
解:∵OA=OP=6,
∴OA=⊙O半径,
∴点A与⊙O的位置关系为:点在圆上.
故选:A.
本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=R时,点在圆上;当d>R时,点在圆外;当d<R时,点在圆内.
8.B
【解析】
先运用圆的切线长定理可以得到:PA=PB,再利用等腰三角形的性质即可求出∠PAB的度数,最后利用切线的性质解题即可.
解:PA,PB是⊙O的切线,
故选:B.
本题考查圆的切线的性质,是重要考点,难度较易,掌握相关知识是解题关键.
9.B
【解析】
直接利用切线的性质得出∠OCD=90°,进而得出∠DOC=50°,进而得出答案.
解:连接OC,
∵DC是⊙O的切线,C为切点,
∴∠OCD=90°,
∵∠D=40°,
∴∠DOC=50°,
∵AO=CO,
∴∠A=∠ACO,
∴∠A=∠DOC=25°.
故选:B.
此题主要考查了切线的性质,正确得出∠DOC=50°是解题关键.
10.B
【解析】
连接AO,BO,
∵PA,PB切⊙O于点A,B,
∴∠PAO=∠PBO=90°,
∵∠P=36°,
∴∠AOB=144°,
∴∠ACB=72°.
故选:B.
11.B
【解析】
根据圆心角,弧,弦的关系对各选项进行逐一判断即可.
解:A、∵∠ACB与∠ACD的大小关系不确定,
∴AB与AD不一定相等,故此选项不符合题意;
B、∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴BC=CD,,故此选项符合题意;
C、∵∠ACB与∠ACD的大小关系不确定,
∴与不一定相等,不符合题意;
D、∠BCA与∠DCA的大小关系不确定,不符合题意.
故答案为:B.
本题考查的是圆心角、弧、弦的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
12.A
【解析】
直接根据直径所对的圆周角为直角进行求解即可.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴在Rt△ABC中,∠B=90°-∠A=70°,
故选:A.
本题考查直径所对的圆周角为直角,理解基本定理是解题关键.
13.C
【解析】
试题分析:由题意可知,∠ABC和∠AOC是同弧所对的圆周角和圆心角,所以∠AOC=2∠ABC,又因为∠ABC+∠AOC=90°,所以∠AOC=60°.
故选C.
考点:圆周角和圆心角.
14.D
【解析】
先根据垂径定理得出AB=2BE,再由CE=4,OB=8得出OE的长,根据勾股定理求出BE的长即可得出结论.
解:∵⊙O的直径CD垂直弦AB于点E,
∴AB=2BE.
∵CE=4,OB=8,
∴OE=8-4=4,
∴BE=,
∴AB=.
故选:D.
本题考查了垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
15.C
【解析】
根据圆内接四边形的性质得到∠D=180°-∠B=120°,根据三角形内角和定理计算即可.
∴∠B=60°,
∵四边形ABCD是圆内接四边形,
∴∠D=180°−∠B=120°,
∴∠ACD=180°−∠DAC−∠D=40°,
故选C.
16.C
【解析】
根据圆周角定理得∠BOC=2∠A=45°,由于⊙O的直径AB垂直于弦CD,根据垂径定理得CE=DE,且可判断△OCE为等腰直角三角形,所以CE=OC=2,然后利用CD=2CE进行计算.
解:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=2,
∴CD=2CE=4.
故选:C.
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰直角三角形的性质和垂径定理.
17.B
【解析】
根据同弧所对的圆心角是圆周角的一半即可求解.
解:∵同弧所对的圆心角是圆周角的一半;
∴
根据圆内接四边形对角互补
故选:B
此题考查的是圆周角定理的应用,掌握圆周角定理是解题的关键.
18.A
【解析】
连接OA,OB,过O作OH⊥AB于H,根据圆周角定理得到∠AOB=2∠ACB=120°,根据等腰三角形的性质得到∠AOH=∠BOH=60°,根据直角三角形的性质得到OH,AH的长,于是得到答案.
解:连接OA,OB,过O作OH⊥AB于H,
∵∠ACB=60°,
∴∠AOB=2∠ACB=120°,
∵OB=OA=8,
∴∠AOH=∠BOH=60°,
∴∠OAB=30°,
∴OH=OA=4,
∴AH= ,
∴AB=2AH=8,
故选:A.
本题考查了三角形的外接圆与外心,等腰三角形的性质,垂径定理,勾股定理,正确的作出辅助线是解题的关键.
19.C
【解析】
先根据正五边形的内角和求出的度数,再利用扇形的面积公式即可得.
解:五边形是边长为6的正五边形,
,
则图中阴影部分的面积为,
故选:C.
本题考查了扇形的面积、正五边形,熟练掌握正五边形的内角和是解题关键.
20.D
【解析】
由垂径定理得AE=AB=4,再由勾股定理得出方程,解方程即可.
解:设⊙O的半径为r,
∵CD是⊙O的直径,AB⊥CD,AB=8,
∴AE=AB=4,
在Rt△OAE中,由勾股定理得:AE2+OE2=OA2,
即42+(r-2)2=r2,
解得:r=5,
即⊙O的半径为5,
故选:D.
本题考查的是垂径定理及勾股定理,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
21.B
【解析】
本题可先由勾股定理等性质算出点与圆心的距离d,再根据点与圆心的距离与半径的大小关系,即当d>r时,点在圆外;当d=r时,点在圆上;点在圆外;当d<r时,点在圆内;来确定点与圆的位置关系.
解:∵点A(﹣4,﹣3),
∴,
∵⊙A的半径为4,
∴,
∴点O在⊙A外;
故选:B
本题考查了点与圆的位置关系及坐标与图形性质,能够根据勾股定理求得点到圆心的距离,根据数量关系判断点和圆的位置关系.
22.D
【解析】
设点E是优弧AB上的一点,连接EA,EB,根据同弧所对的圆周角是圆心角的一半可求得∠E的度数,再根据圆内接四边形的对角互补即可得到∠ACB的度数.
解:设点E是优弧AB上的一点,连接EA,EB,
∵∠AOB=100°,
∴∠E=∠AOB=50°,
∴∠ACB=180°-∠E=130°.
故选:D.
本题考查了圆周角定理,以及圆内接四边形的性质,知道同弧所对的圆周角是圆心角的一半是解题的关键.
23.B
【解析】
解:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF=∠BOF=15°
故选B
24.C
【解析】
由AC是⊙的切线可得∠CAB=,又由,可得∠ABC=40;再由OD=OB,则∠BDO=40最后由∠AOD=∠OBD+∠OBD计算即可.
解:∵AC是⊙的切线
∴∠CAB=,
又∵
∴∠ABC=-=40
又∵OD=OB
∴∠BDO=∠ABC=40
又∵∠AOD=∠OBD+∠OBD
∴∠AOD=40+40=80
故答案为C.
本题考查了圆的切线的性质、等腰三角形以及三角形外角的概念.其中解题关键是运用圆的切线垂直于半径的性质.
25.B
【解析】
连接OC交AB于D,根据圆的性质和垂径定理可知OC⊥AB,AD=BD=3,根据勾股定理求得OD的长,由CD=OC﹣OD即可求解.
解:根据题意和圆的性质知点C为的中点,
连接OC交AB于D,则OC⊥AB,AD=BD=AB=3,
在Rt△OAD中,OA=4,AD=3,
∴OD===,
∴CD=OC﹣OD=4﹣,
即点到弦所在直线的距离是(4﹣)米,
故选:B.
本题考查圆的性质、垂径定理、勾股定理,熟练掌握垂径定理是解答的关键.
26.A
【解析】
先利用勾股定理判断△ABC为直角三角形,且∠BAC=90°,继而证明四边形AEOF为正方形,设⊙O的半径为r,利用面积法求出r的值即可求得答案.
∵AB=5,BC=13,CA=12,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,且∠BAC=90°,
∵⊙O为△ABC内切圆,
∴∠AFO=∠AEO=90°,且AE=AF,
∴四边形AEOF为正方形,
设⊙O的半径为r,
∴OE=OF=r,
∴S四边形AEOF=r²,
连接AO,BO,CO,
∴S△ABC=S△AOB+S△AOC+S△BOC,
∴,
∴r=2,
∴S四边形AEOF=r²=4,
故选A.
本题考查了三角形的内切圆,勾股定理的逆定理,正方形判定与性质,面积法等,正确把握相关知识是解题的关键.
27.C
【解析】
连接OC,由圆周角定理可知,又由DC是⊙O切线,可知,根据直角三角形中两锐角互余,即可求得答案.
解:连接OC,如下图:
∵,
∴
又∵DC切⊙O于点C,OC为半径
∴
∴是直角三角形
∴
∴
故选:C
本题考查切线的性质定理,圆周角定理,以及直角三角形性质,牢记相关知识点,数形结合解题是关键.
28.A
【解析】
如图,连接OB、OC.首先证明△OBC是等边三角形,求出BC、BM,根据勾股定理即可求出OM.
解:如图,连接OB、OC.
∵ABCDEF是正六边形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等边三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,,
故选:A.
本题考查正多边形与圆、等边三角形的性质、勾股定理、弧长公式等知识,解题的关键是记住等边三角形的性质,弧长公式,属于基础题,中考常考题型.
29.D
【解析】
比较圆心到直线距离与圆半径的大小关系,进行判断即可.
圆的直径是13cm,故半径为6.5cm. 圆心与直线上某一点的距离是6.5cm,那么圆心到直线的距离可能等于6.5cm也可能小于6.5cm,因此直线与圆相切或相交.故选D.
本题主要考查直线与圆的位置关系,需注意圆的半径为6.5cm,那么圆心与直线上某一点的距离是6.5cm是指圆心到直线的距离可能等于6.5cm也可能小于6.5cm.
30.D
【解析】
连接AO,设直径CD的长为寸,则半径OA=OC=寸,然后利用垂径定理得出AE,最后根据勾股定理进一步求解即可.
如图,连接AO,
设直径CD的长为寸,则半径OA=OC=寸,
∵CD为的直径,弦,垂足为E,AB=10寸,
∴AE=BE=AB=5寸,
根据勾股定理可知,
在Rt△AOE中,,
∴,
解得:,
∴,
即CD长为26寸.
本题主要考查了垂径定理与勾股定理的综合运用,熟练掌握相关概念是解题关键.
31.C
【解析】
如图,首先证得OA⊥BC;然后由圆周角定理推知∠C=30°,通过解直角△ACD可以求得CD的长度.则BC=2CD.
解:设AO与BC交于点D.
∵∠AOB=60°,,
∴∠C=∠AOB=30°,
又∵AB=AC,
∴
∴AD⊥BC,
∴BD=CD,
∴在直角△ACD中,CD=AC•cos30°=2×=,
∴BC=2CD=2.
故选C.
本题考查了圆周角定理,也考查了解直角三角形.题目难度不大.
32.C
【解析】
如图1中,取AB的中点O,连接OG,OC.首先证明O,G,C共线时,CG的值最小(如图2中),证明CF=CG=BH即可解决问题(图2中).
解:如图中,取的中点,连接,.
四边形是正方形,
,
,
,
,
,
,
∴点G在以AB为圆的圆的上运动,
,
,
,
当,,共线时,的值最小,CG最小值(如图2中),
,
,
∵四边形ABCD为正方形,
∴,
,
,
,
,
,
,,
,
,
,
,
,
故选择:C.
本题考查正方形的性质,全等三角形的判定和性质,直角三角形斜边中线的性质,直径所对圆周角的性质,点C到圆上最短距离,等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形与辅助圆解决问题,属于中考选择题中的压轴题.
33.A
【解析】
根据切线的性质由AB与⊙O相切得到OB⊥AB,则∠ABO=90°,利用∠A=30°得到∠AOB=60°,再根据三角形外角性质得∠AOB=∠C+∠OBC,由于∠C=∠OBC,所以∠C=∠AOB=30°.
解:连结OB,如图,
∵AB与⊙O相切,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∵∠AOB=∠C+∠OBC,
而∠C=∠OBC,
∴∠C=∠AOB=30°.
故选A.
此题考查了切线的性质:圆的切线垂直于经过切点的半径;以及圆周角定理:等弧所对的圆周角等于所对圆心角的一半.
34.D
【解析】
∵⊙O内切于四边形ABCD,
∴AD+BC=AB+CD,
∵AB=10,BC=7,CD=8,
∴AD+7=10+8,
解得:AD=11.
故选D.
35.C
【解析】
利用圆锥的侧面展开图为扇形,且这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长以及弧长公式即可列出关于l的方程,解出l即可.
解:根据题意得,,
解得,,
即该圆锥母线的长为6.
故选:C.
本题考查关于圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
36.D
【解析】
先利用直径所对的圆周角是直角得到∠ACB=90°,从而求出∠CAB,再利用同弧所对的圆周角相等即可求出∠BDC.
解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=35°,
∴∠CAB=55°,
∴∠BDC=∠CAB=55°.
故选:D.
本题考查了圆周角定理的推论,即直径所对的圆周角是90°和同弧或等弧所对的圆周角相等,解决本题的关键是牢记相关概念与推论.
37.C
【解析】
连接OA,OB根据切线的性质定理,切线垂直于过切点的半径,即可求得∠OAP,∠OBP的度数,根据四边形的内角和定理即可求的∠AOB的度数,然后根据圆周角定理即可求解.
∵PA是圆的切线,
∴
同理
根据四边形内角和定理可得:
∴
故选:C.
考查切线的性质以及圆周角定理,连接圆心与切点是解题的关键.
38.B
【解析】
欲求直线l与圆O的位置关系,关键是比较圆心到直线的距离d与圆半径r的大小关系.若d<r,则直线与圆相交;若d=r,则直线与圆相切;若d>r,则直线与圆相离.
解:∵圆半径r=3,圆心到直线的距离d=5.
故r=3<d=5,
∴直线与圆的位置关系是相离.
故选:B.
本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.
39.D
【解析】
根据题意可知,四边形OACB是矩形,D为AB的中点,连接OC,可知D点是矩形的对角线的交点,那么当C点绕圆O旋转一周时,D点也会以OD长为半径旋转一周,D点的轨迹是一个以O为圆心,以OD长为半径的圆,计算圆的周长即可.
如图,连接OC,
∵CA⊥x轴,CB⊥y轴,
∴四边形OACB是矩形,
∵D为AB中点,
∴点D在AC上,且OD=OC,
∵⊙O的半径为2,
∴如果点C在圆上运动一周,那么点D运动轨迹是一个半径为1圆,
∴点D运动过的路程长为2π•1=2π,
故选:D.
本题考查了动点问题,解决本题的关键是能够判断出D点的运动轨迹是一个半径为1的圆.
40.B
【解析】
首先根据题意画出图形,即可得△OBC是等边三角形,又由正六边形ABCDEF的周长为6,即可求得BC的长,继而求得△OBC的面积,则可求得该六边形的面积.
解:如图,连接OB,OC,过O作OM⊥BC于M,
∴∠BOC=×360°=60°,
∵OB=OC,
∴△OBC是等边三角形,
∵正六边形ABCDEF的周长为6,
∴BC=6÷6=1,
∴OB=BC=1,
∴BM=BC=,
∴OM= ,
∴S△OBC=×BC×OM= ,
∴该六边形的面积为: .
故选:B.
此题考查了圆的内接六边形的性质与等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
41.B
【解析】
根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积.即阴影部分的面积就等于扇形ABB′的面积.
由旋转的性质可知:以AB′为直径的半圆的面积=以AB为直径的半圆的面积,再根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.
则阴影部分的面积是:π.
故选B.
本题考查了扇形的面积的计算以及旋转的性质,培养了学生的计算能力和观察图形的能力,运用面积的和差求不规则图形的面积是解题的关键.
42.A
【解析】
根据题意,利用勾股定理,先求出弦长的一半,进而求出弦长.
解:如图
由题意知,OA=4,OD=CD=2,OC⊥AB,
∴AD=BD,
在Rt△AOD中,,
∴.
故选:A.
本题考查了垂径定理,在求弦长时,往往通过构造直角三角形,利用勾股定理,先求出弦长的一半,再求得弦长.此类问题极易出错,要特别注意.
43.A
【解析】
如图,根据∠BAC=90°,可确定BC是⊙O的直径,故OA=OB=OC=,计算AB=AC=2,根据扇形面积公式计算即可.
如图,∵∠BAC=90°,AB=AC,
∴BC是⊙O的直径,∠ABC=∠ACB =45°,
∴OA=OB=OC=,AO⊥BC,
∴AB=AC==2,
∴扇形面积为:=π.
故选A.
本题考查了扇形的面积,90°的圆周角所对的弦是直径,等腰直角三角形的判定,灵活运用90°的圆周角所对的弦是直径,计算出扇形的半径是解题的关键.
44.A
【解析】
如图,连接BO,FO,OA.则△OAF,△AOB都是等边三角形,即可证明AB∥OF,从而得到△OAB的面积=△ABF的面积,则阴影部分的面积=扇形OAB的面积×3,由此求解即可.
解:如图,连接BO,FO,OA.
由题意得,△OAF,△AOB都是等边三角形,
∴∠AOF=∠OAB=60°,
∴AB∥OF,
∴△OAB的面积=△ABF的面积,
∵六边形ABCDEF是正六边形,
∴AF=AB=OA=OB=,
∴阴影部分的面积=扇形OAB的面积×3=×3=.
故选:A.
本题主要考查了正多边形与圆,等边三角形的性质与判定,平行线的性质与判定,扇形面积,得到△OAB的面积=△ABF的面积是解题的关键.
45.D
【解析】
根据圆周角和圆心角的关系,可以得到的度数,然后根据为的切线和直角三角形的两个锐角互余,即可求得的度数.
解:,
,
为的切线,点为切点,
,
,
故选:D.
本题考查切线的性质、圆周角定理、直角三角形的性质,解题的关键是利用数形结合的思想解答.
46.D
【解析】
如图,连接OQ,作CH⊥AB于H.首先证明点Q的运动轨迹为以AO为直径的⊙K,连接CK,当点Q在CK的延长线上时,CQ的值最大,利用勾股定理求出CK即可解决问题.
解:如图,连接OQ,作CH⊥AB于H.
∵AQ=QP,
∴OQ⊥PA,
∴∠AQO=90°,
∴点Q的运动轨迹为以AO为直径的⊙K,连接CK,
当点Q在CK的延长线上时,CQ的值最大,
在Rt△OCH中,∵∠COH=60°,OC=2,
∴OH= OC=1,CH=,
在Rt△CKH中,CK= =,
∴CQ的最大值为1+,
故选D.
本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识,解题的关键是正确寻找点Q的运动轨迹,学会构造辅助圆解决问题,属于中考填空题中的压轴题.
47.B
【解析】
根据题意可知P在BA延长线与的交点时此时长的最大,进而证明,最后即可求出长的最大值.
解:如图,可知P在BA延长线与的交点时此时长的最大,证明如下:
连接BP,
∵,
∴BD=DC,
∵是的中点,
∴DE//BP, ,
所以当BP的长最大时,长的最大,
由题意可知P在BA延长线与的交点时BP的长最大此时长的最大,
∵BC=6,AD=4,
∴BD=DC=3,BA=5,
∵的半径为2,即AP=2,
∴BP=5+2=7,
∴.
故选:B.
本题考查圆的动点问题,熟练掌握圆的性质并利用中位线性质得出是解题的关键.
48.C
【解析】
根据抛物线解析式可求得点A(-4,0),B(4,0),故O点为AB的中点,又Q是AP上的中点可知OQ=BP,故OQ最大即为BP最大,即连接BC并延长BC交圆于点P时BP最大,进而即可求得OQ的最大值.
解:连结BP,
∵抛物线与轴交于A、两点,
当y=0时,,
解得,
∴A(-4,0),B(4,0),即OA=4,
在直角△COB中,
BC=,
∵Q是AP上的中点,O是AB的中点,
∴OQ为△ABP中位线,即OQ=BP,
又∵P在圆C上,且半径为2,
∴当B、C、P共线时BP最大,即OQ最大,
此时BP=BC+CP=5+2=7,
OQ=BP=.
故选择C.
本题考查了勾股定理求长度,二次函数解析式求点的坐标及线段长度,中位线,点到圆上最长的距离,解本题的关键是将求OQ最大转化为求BP最长时的情况.
初中人教版第十三章 轴对称综合与测试习题: 这是一份初中人教版第十三章 轴对称综合与测试习题,共33页。
2021学年第二十五章 概率初步综合与测试达标测试: 这是一份2021学年第二十五章 概率初步综合与测试达标测试,共25页。
人教版第二十四章 圆综合与测试习题: 这是一份人教版第二十四章 圆综合与测试习题,共91页。














