2021学年2.5 直线与圆、圆与圆的位置教学演示课件ppt

这是一份2021学年2.5 直线与圆、圆与圆的位置教学演示课件ppt，共34页。PPT课件主要包含了代数法，联立求解，两圆相交，两圆相切，③方程组没有实数解，两圆相离或内含，由两个圆的方程，几何法，①-②得，C-12等内容，欢迎下载使用。

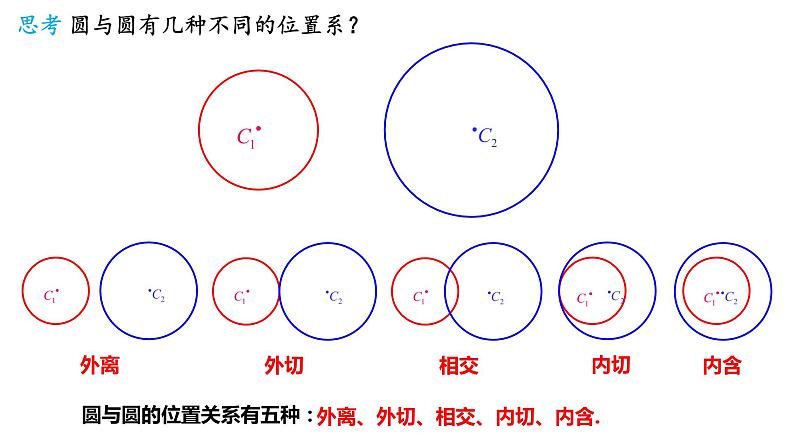
思考 圆与圆有几种不同的位置系？
圆与圆的位置关系有五种：
外离、外切、相交、内切、内含.
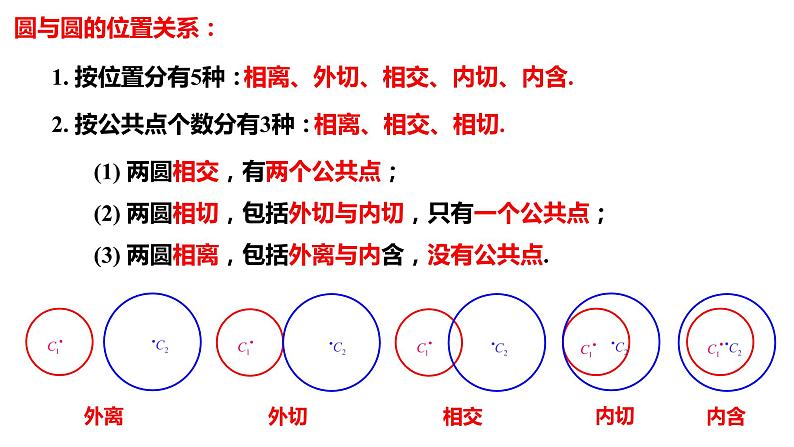
(1) 两圆相交，有两个公共点；(2) 两圆相切，包括外切与内切，只有一个公共点；(3) 两圆相离，包括外离与内含，没有公共点.
1. 按位置分有5种：
相离、外切、相交、内切、内含.
2. 按公共点个数分有3种：
利用圆的方程判断圆与圆位置关系：
① 方程组有两组不同实数解
② 方程组有一组实数解
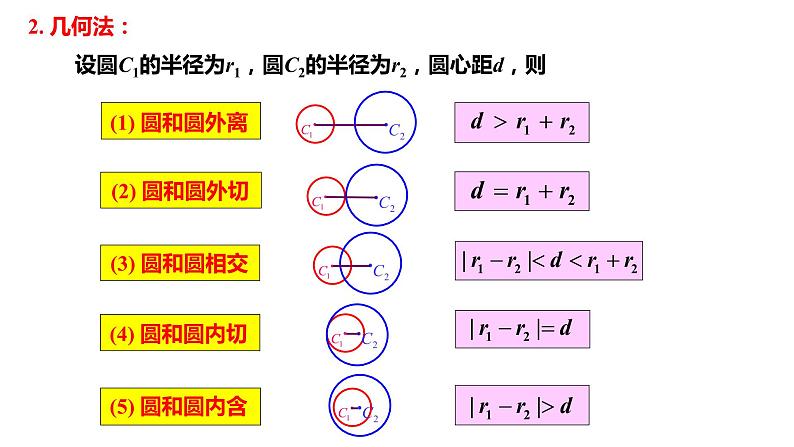
思考1 类比运用直线和圆的方程，研究直线与圆的位置关系的方法，如何利用圆的方程，判断它们之间的位置关系?
设圆C1的半径为r1，圆C2的半径为r2，圆心距d，则
解法1: 将圆C1与圆C2的方程联立，得到方程组
联立①③，消去y，可得
方程④的根的判别式△>0，所以，方程④有两个不相等的实数根x1，x2.把x1，x2分别代人方程③，得到y1，y2. 因此圆C1与圆C2有两个公共点A(x1，y1)，B(x2，y2)，这两个圆相交.
解法2: 把圆C1与圆C2的方程分别化成标准方程，得
∴圆C1与圆C2相交.
解: 把圆C2方程化成标准方程，得
∴圆C1与圆C2外切.
思考2 在代数法中，如果两圆方程联立消元后得到的方程的∆＝0，它说明什么?你能据此确定两圆是内切还是外切吗? 如何判断两圆是内切还是外切呢? 当∆<0时，两圆是什么位置关系?
当∆＝0时, 方程组只有一组解, 此时两圆相切, 但不能确定两圆是内切还是外切.
要判断两圆是内切还是外切, 则需看圆心位置, 若较小圆的圆心在另一个圆内, 则两圆内切；否则, 两圆外切. 或者用几何法直接比较圆心距与两圆半径和或差的大小, 若圆心距等于两圆半径和, 则两圆外切, 圆心距等于两圆半径差的绝对值, 则两圆内切.
当∆< 0时, 方程组没有解, 此时两圆相离，但不能确定两圆是外离还是内含.
要判断两圆是外离还是内含, 同样需看圆心位置, 若较小圆的圆心在另一个圆内, 则两圆内含; 否则, 两圆外离. 或者用几何法直接比较圆心距与两圆半径和或差的大小, 若圆心距大于两圆半径和, 则两圆外离, 圆心距小于两圆半径差的绝对值, 则两圆内含.
巩固训练1 当实数k为何值时，两圆C1：x2＋y2＋4x－6y＋12＝0，C2：x2＋y2－2x－14y＋k＝0相交、相切、相离？
解: 如图示，以线段AB的中点O为原点建立平面直角坐标系.由AB=4，得A(一2, 0)，B(2, 0).
解法1: 把圆C1与圆C2的方程分别化成标准方程，得
把圆C1与圆C2的方程相减，得
∴圆C1与圆C2的公共弦所在直线的方程为
1. 若两圆相交，则过交点的圆系方程为
2. 若两圆相切(内切或外切), 则公切线所在直线方程为
注意：① λ为参数, 圆系中不包括圆C2; ② 当λ＝－1时, 方程两圆的公共弦所在直线方程, 即
(也就是两圆方程相减所得)
解1: 将圆C1与圆C2的方程联立，得到方程组
解2: 将圆C1与圆C2的方程相减，可得公共弦所在直线l的方程为
公共弦长的求法:1. 代数法： 将两圆的方程联立，解出交点坐标，利用两点间的距离公式求出弦长．2. 几何法： 求出公共弦所在直线的方程，利用圆的半径、半弦长、弦心距构成的直角三角形，根据勾股定理求解．
得直线与圆的交点坐标为
故面积最小的圆的方程：
【典例】已知⊙C: (x－1)2＋(y－2) 2＝2, P(2,－1), 过P作⊙C的切线, 切点为A, B. 求: (1) 直线PA、PB的方程； (2) 过点P与⊙C相切的切线长； (3) ∠APB的余弦； (4) 以PC为直径的圆的方程； (5) 直线AB的方程.
【典例】已知⊙C: (x－1)2＋(y－2) 2＝2, P(2,－1), 过P作⊙C的切线, 切点为A, B. 求: (1) 直线PA、PB的方程；
【典例】已知⊙C: (x－1)2＋(y－2) 2＝2, P(2,－1), 过P作⊙C的切线, 切点为A, B. 求: (2) 过点P与⊙C相切的切线长；
(3) 取两切线PA、PB的方向向量分别为
【典例】已知⊙C: (x－1)2＋(y－2) 2＝2, P(2,－1), 过P作⊙C的切线, 切点为A, B. 求: (3) ∠APB的余弦；
∴ 以PC为直径的圆的圆心坐标为 半径为
【典例】已知⊙C: (x－1)2＋(y－2) 2＝2, P(2,－1), 过P作⊙C的切线, 切点为A, B. 求: (4) 以PC为直径的圆的方程；
∴ 以PC为直径的圆方程为：
【典例】已知⊙C: (x－1)2＋(y－2) 2＝2, P(2,－1), 过P作⊙C的切线, 切点为A, B. 求: (5) 直线AB的方程.