人教A版 (2019)必修 第二册第七章 复数7.1 复数的概念教课内容课件ppt

这是一份人教A版 (2019)必修 第二册第七章 复数7.1 复数的概念教课内容课件ppt，共32页。PPT课件主要包含了复习上节课，复数的概念，复数的代数形式，一般用字母C表示，复数za+bi，实数的几何意义，新课导入，数轴上的点，一个复数由什么确定，复数的几何意义一等内容，欢迎下载使用。

一句话，负实数开平方到底得到什么东西？
注：一元三次方程的求根公式百度就有。
引入
反思：虽然有实数满足已知等式，但不必求出x。
讨论关于x的方程（x-1）(2x-1)(x2-2)(x2+1)=0的解的个数。分别在整数范围内、有理数范围内、实数范围内有几解？
在宗教比如佛教中，人往往把鬼、神形象化、具体化、实物化，那就是给让人敬畏的鬼、神塑一座雕像。在寺庙，在画家的名画中。许多画家以画宗教中的鬼、神为荣。 我们发现的新数是鬼或是神，你看不见摸不着，你只能想象，于是为了形象化、具体化、实物化我们像宗教人士为鬼、神塑造一座雕像样让i表示这个幽灵一样的数。i像宗教人士为鬼、神立像。 实数是看得见摸得着的。
参考文献：杂志《中学数学教学参考》2011第九期上旬里面的一篇论文《“数系的扩充”一课的教学设计》作者：丁箐（南京师范大学附属中学）
注：x=i或-i说明有两个鬼或神。
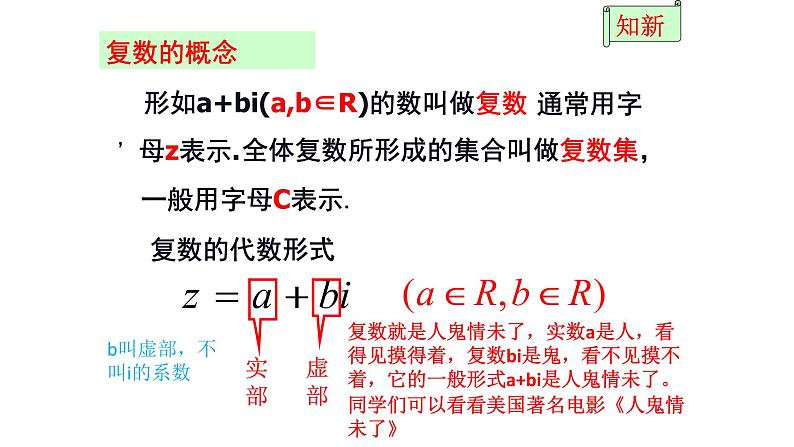
　形如a+bi(a,b∈R)的数叫做复数,
全体复数所形成的集合叫做复数集，
复数就是人鬼情未了，实数a是人，看得见摸得着，复数bi是鬼，看不见摸不着，它的一般形式a+bi是人鬼情未了。同学们可以看看美国著名电影《人鬼情未了》
b叫虚部，不叫i的系数
2. 复数集、虚数集、实数集、纯虚数集之间的关系
同学们，这些名字是数学家取的，是取的形象生动深刻，我们一看到名字就知道是什么意思。实数看得见摸得着，全是人，非纯虚数是半人半鬼或半人半仙，纯虚数是全是鬼。“纯”就是纯净没有杂质的意思。实：就是看得见摸得着的意思。虚：就是看不见摸不着的意思。
3.规定：如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等．
2) 两个虚数只能说相等或不相等，而不能比较大小.
复数的发展史 虚数这种假设,是需要勇气的,人们在当时是无法接受的,认为她是想象的,不存在的,但这丝毫不影响数学家对虚数单位 的假设研究:第一次认真讨论这种数的是文艺复兴时期意大利有名的数学“怪杰”卡丹，他是1545年开始讨论这种数的，当时复数被他称作“诡辩量”.几乎过了100年，笛卡尔才给这种“虚幻之数”取了一个名字——虚数．但是又过了140年，欧拉还是说这种数只是存在于“幻想之中”，并用 （imaginary，即虚幻的缩写）来表示它的单位. 后来德国数学家高斯给出了复数的定义，但他们仍感到这种数有点虚无缥缈，尽管他们也感到它的作用．1830年，高斯详细论述了用直角坐标系的复平面上的点表示复数 ，使复数有了立足之地,人们才最终承认了复数.到今天复数已经成为现代科技中普遍运用的数学工具之一.
同学们看下面几个复数：1+2i、3-2i、5+6i。我们知道复数像鬼、神看不见、摸不着，你只能想象。于是一些宗教的人士为了吸引大众入教也为了宗教能够普及，给一些鬼、神塑立雕像，这雕像能让看不见摸不着的鬼神形象、具体、直观、实物，能让人看得见摸得着。 我们上节课讲过这些记号1+2i、3-2i、5+6i是给复数这个鬼、神立雕像，能让复数形象、具体、直观、实物。但同学们注意用1+2i、3-2i、5+6i表示这些鬼神人们还是觉得太抽象太难想象太虚无缥缈太云里雾里太朦朦胧胧，复数刚诞生时文艺复兴时期意大利有名的数学“怪杰”卡丹，他是1545年开始讨论这种数的，当时复数被他称作“诡辩量”.几乎过了100年，笛卡尔才给这种“虚幻之数”取了一个名字——虚数．就算过了140年欧拉还是说这种数只是存在于“幻想之中”，并用（imaginary，即虚幻的缩写）来表示它的单位。 于是数学家想有没有可能给这种幻想之中的数形象化、具体化、直观化、实物化？像宗教人士给看不见摸不着的鬼神形象化、具体化、直观化，实物化。给复数进一步的形象化、具体化、直观化、实物化，这是高斯的功劳
7.1.2复数的几何意义
在几何上，我们用什么来表示实数?
实数可以用数轴上的点来表示.
Z=a+bi(a, b∈R)
你能否找到用来表示复数的几何模型呢？
任何一个复数z=a+bi，都可以由一个有序实数对(a,b)唯一确定.由于有序实数对(a,b)与平面直角坐标系中的点一一对应，因此复数集与平面直角坐标系中的点集之间可以建立一一对应.
直角坐标系中的点Z(a,b)
可用下图表示他们彼此的关系:
因此，复数集与平面直角坐标系中的点集之间可以建立一一对应.
那么现在复数z=a+bi可以在平面直角坐标系中表示出来，如图所示：
复数z=a+bi用点Z(a,b)表示.
建立了平面直角坐标系来表示复数的平面
------复数平面 (简称复平面)
原点即在x轴又在y轴，所以原点即在实轴又在虚轴。实轴上全是人，虚轴上除原点外全是鬼。一、二、三、四象限半人半鬼。
复平面内的点Z(a,b)
复数的几何意义之一是：
实轴上的点都表示实数；虚轴上的点除原点外，都表示纯虚数，因为原点表示实数0.
复平面内的原点(0,0)表示( );
实轴上的点(2,0)表示( )；
虚轴上的点(0,-1)表示( );
点(-2,3)表示( ).
在平面直角坐标系中，每一个平面向量都可以用一个有序实数对来表示，而有序实数对与复数是一一对应的.这样，我们还可以用平面向量来表示复数.
可用下图表示他们彼此的关系：
现在我们就用平面向量来表示复数，如图所示：
由此可知，复数集C和复平面内的向量所成的集合也是一一对应的.
复数的几何意义之二是：
口答：说出下列复数的共轭复数
( =2-3i )
( =6i )
注意：⑴当虚部不为0时的共轭复数称为 共轭虚数 ⑵实数的共轭复数是它本身
解：⑴作图得出结论：在复平面内共轭复数z1 ,z2所对应的点关于实轴对称。
若z1,z2是共轭复数，那么⑴在复平面内，它们所对应的点有怎的位置关系？⑵z1·z2是一个怎样的数？
⑵令z1=a+bi,则z2=a-bi则z1·z2=(a+bi)(a-bi) =a2-abi+abi-bi2 =a2+b2结论：任意两个互为共轭复数的乘积是一个实数.
例1：已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限，求实数m的取值范围。
变式：已知复数z=(m2+m-6)+(m2+m-2)i 在复平面内所对应的点在直线x-2y+4=0上，求实数m的值。
解：∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是（m2+m-6，m2+m-2），
∴(m2+m-6)-2(m2+m-2)+4=0，
∴m=1或m=-2。
同学们这相当于高考容易题，高考容易题通过训练都会做。90分容易题都会做，考个专科没问题。
1.复数的实质是一对有序实数对；
2.用平面直角坐标系表示复平面，其中x轴叫做实轴，y轴叫做虚轴；实轴上的点都表示实数；除了原点外，虚轴上的点都表示纯虚数；