数学九年级下册27.3 位似教学设计及反思

这是一份数学九年级下册27.3 位似教学设计及反思，共9页。

知识点一 位似图形
要点1.位似图形的定义
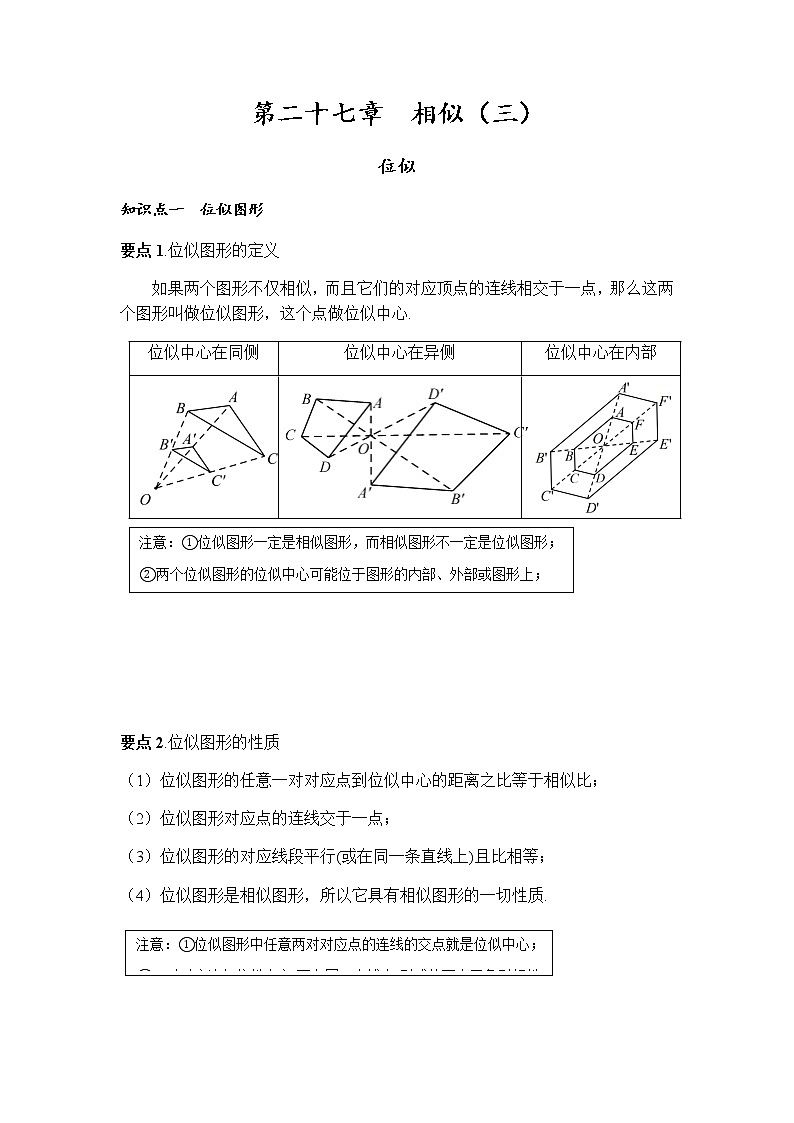
如果两个图形不仅相似，而且它们的对应顶点的连线相交于一点，那么这两个图形叫做位似图形，这个点做位似中心.
注意：①位似图形一定是相似图形，而相似图形不一定是位似图形；
②两个位似图形的位似中心可能位于图形的内部、外部或图形上；
③两个位似图形可能位于位似中心的两侧，也可能于位似中心的一侧.
要点2.位似图形的性质
（1）位似图形的任意一对对应点到位似中心的距离之比等于相似比；
（2）位似图形对应点的连线交于一点；
（3）位似图形的对应线段平行(或在同一条直线上)且比相等；
（4）位似图形是相似图形，所以它具有相似图形的一切性质.
注意：①位似图形中任意两对对应点的连线的交点就是位似中心；
②一对对应边与位似中心(不在同一直线上)形成的两个三角形相似.
注意：①符合条件的位似图形往往不唯一；
②作出的位似图形一般有两种情况，一是各对应点在位似中心的同侧，二是各对应点在位似中心的两侧；
③作位似图形时，要注意相似比的顺序性.
要点3.位似图形的画法
步骤：①确定位似中心；
②分别过位似中心和原图的各关键点作直线；
③根据相似比，找出所作位似图形的对应点；
④按原图连接各点，得到放大或缩小的图形.
课堂练习
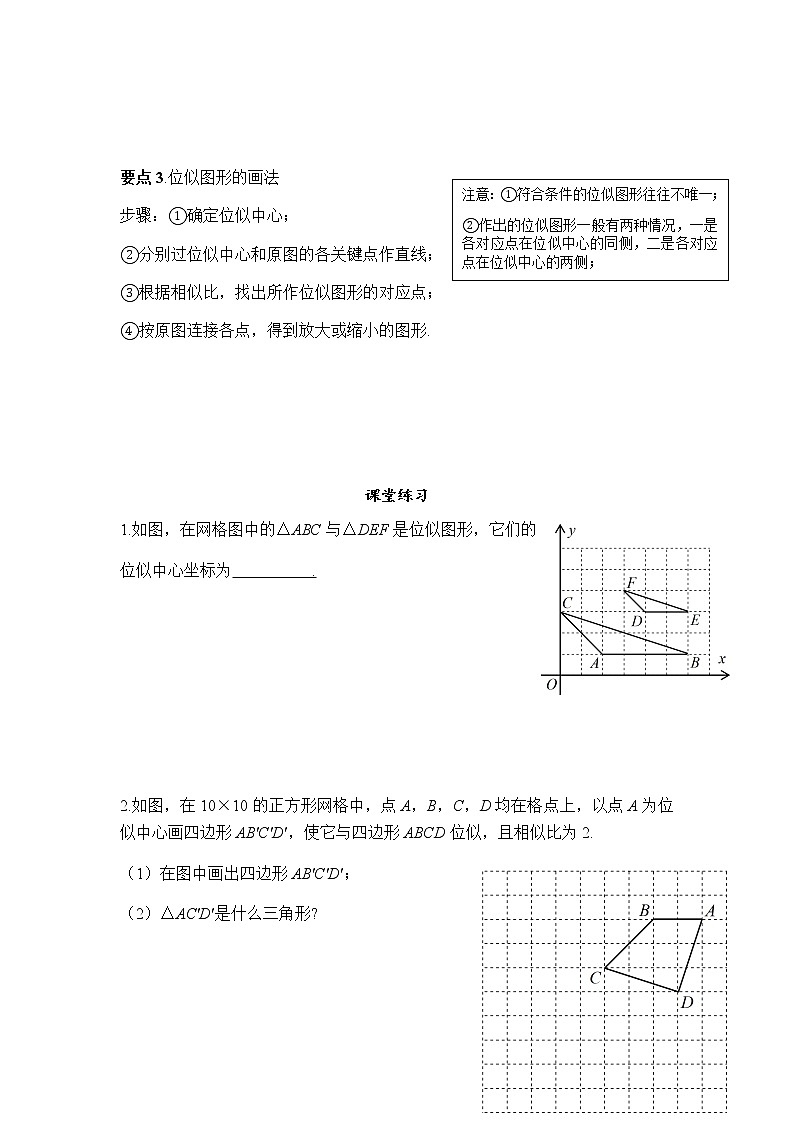
1.如图，在网格图中的△ABC与△DEF是位似图形，它们的
位似中心坐标为 .
2.如图，在10×10的正方形网格中，点A，B，C，D均在格点上，以点A为位似中心画四边形AB'C'D'，使它与四边形ABCD位似，且相似比为2.
（1）在图中画出四边形AB'C'D'；
（2）△AC'D'是什么三角形?
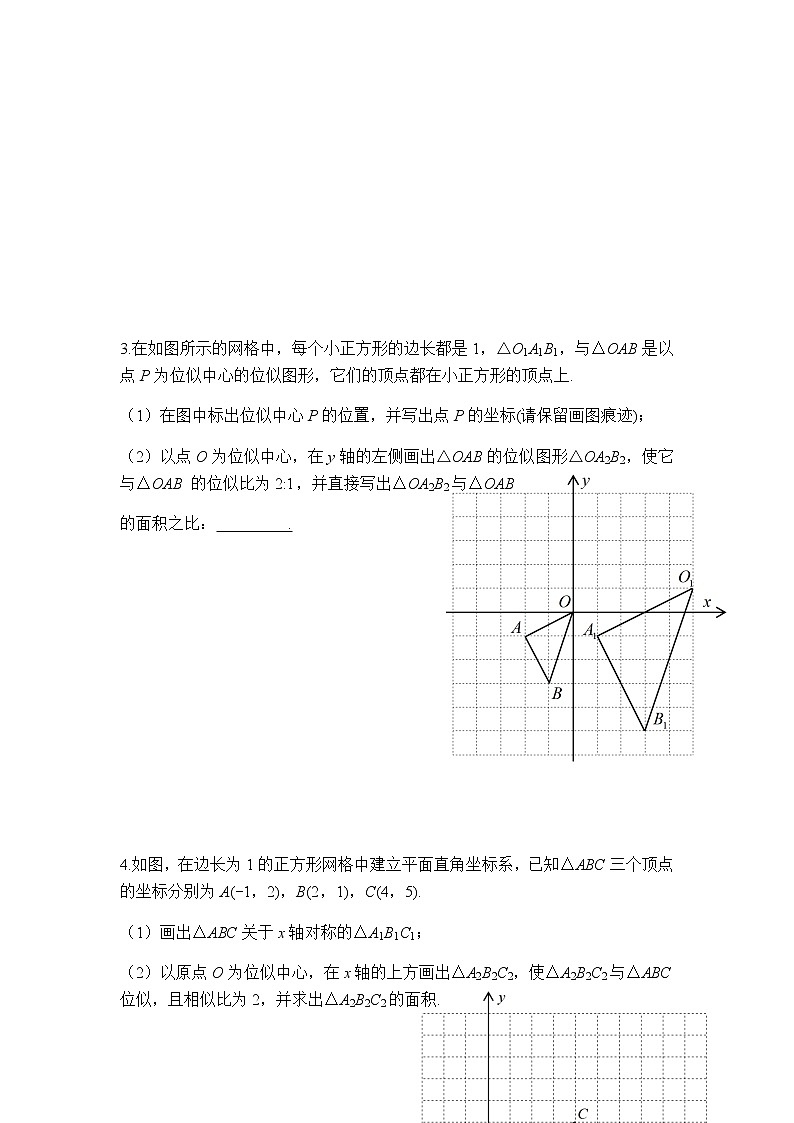
3.在如图所示的网格中，每个小正方形的边长都是1，△O1A1B1，与△OAB是以点P为位似中心的位似图形，它们的顶点都在小正方形的顶点上.
（1）在图中标出位似中心P的位置，并写出点P的坐标(请保留画图痕迹)；
（2）以点O为位似中心，在y轴的左侧画出△OAB的位似图形△OA2B2，使它与△OAB 的位似比为2:1，并直接写出△OA2B2与△OAB
的面积之比： .
4.如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点的坐标分别为A(-1，2)，B(2，1)，C(4，5).
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以原点O为位似中心，在x轴的上方画出△A2B2C2，使△A2B2C2与△ABC位似，且相似比为2，并求出△A2B2C2的面积.
5.在平面直角坐标系中，△OAB 的顶点坐标分别为O(0，0)、A(2，1)、B(1，-2)。
（1）以原点O为位似中心，在y轴的右侧画出△OAB 的一个位似△OA1B1，使它与△OAB 的相似比为2:1， 并写出点A的对应点A1的坐标；
（2）画出将△OAB 向左平移2个单位，再向上平移1个单位后的△O2A2B2，并写出点A2的坐标；
（3）判断△OA1B1与△O2A2B2，能否是关于某一点M为位似中心的位似图形？若是，请在图中标出位似中心M，并写出点M的坐标。
6.平面直角坐标系中，△ABC的三个顶点坐标分别为A(1，-2)，B(2，-1)，C(4，-3)
（1）画出△A1B1C1，使它与△ABC关于x轴对称；
（2）以原点为位似中心，在第一象限画出△A1B1C1的位似图形△A2B2C2使△A2B2C2与
△A1B1C1的相似比为2:1；
（3）若将△A2B2C2绕原点顺时针旋转90°
得到△A3B3C3，求点C2经过的路径长.
7.如图，△ABC的三个顶点坐标分别为A(2，3)，B(3，1)，C(5，4).
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以点P(1，-1)为位似中心，在如图所示的网格中画出△A1B1C1的位似图形△A2B2C2，使△A2B2C2与△A1B1C1的相似比为2:1；
（3）画出△ABC绕点C逆时针旋转90°所
得的△A'B'C'，并写出线段BC扫过的面积.
知识点二 平面直角坐标系中的位似变换
要点1.平面直角坐标系中的位似变换
一般地，在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x0，y0)对应的位似图形上的点的坐标为(kx0，ky0)或(-kx0，-ky0).
要点2.平移、轴对称、旋转、位似变换中坐标的变化规律
课堂练习
1.如图，在直角坐标系中，有两点A(6，3)、B(6，0).以原点
O为位似中心，相似比为，在第一象限内把线段AB缩小
后得到线段CD，则点C的坐标为 .
2.如图，线段AB两个端点的坐标分别为A(6，6)、B(8，2)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C的坐标为（ ）
A.(3，3)B.(4，3)
C.(3，1)D.(4，1)
3.如图，点P(8，6)在△ABC的边AC上，以原点O为位似中心，在第一象限内将△ABC缩小到原来的，得到△A'B'C'，点P在A'C'上的对应点P'的坐标为（ ）
A.(4，3) B.(3，4)
C.(5，3) D.(4，4)
4.如图，已知△AOB和△A1OB1是以点O为位似中心的位似图形，且△AOB和△A1OB1的周长之比为1:2，点B的坐标为(-1，2)，则点B1的坐标为（ ）
A.(2，-4)B.(1，-4)
C.(-1，4)D.(-4，2)
5.如图，四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形，若OA:OA'=2:3，则四边形ABCD和四边形A'B'C'D'的面积比为（ ）
A.4:9 B.2:5
C.2:3 D.
6.在平面直角坐标系中，已知点A(-4，2)，B(-6，-4)，以原点O为位似中心，相似比为2，把△ABO放大，则点A的对应点A'的坐标是 位似中心在同侧
位似中心在异侧
位似中心在内部
图形变换类型
图形
点的坐标变化规律
平移
变换
形状、大小不变，
位置改变
左右平移：横坐标左减右加，纵坐标不变
上下平移：纵坐标上加下减，横坐标不变
轴对称
变换
x轴对称
形状、大小不变，
位置改变
横坐标不变，纵坐标互为相反数
y轴对称
纵坐标不变，横坐标互为相反数
旋转
变换
中心（原点）对称（旋转角是180°）
形状、大小不变，
位置改变
横、纵坐标均与原坐标互为相反数
旋转角不是180°
坐标按全等知识计算
位似变换
（坐标原点为位似中心）
形状不变，
大小、位置改变
若与原图形的相似比为k，则对应点坐标为原来的k倍或者(k≠0).