初中数学沪科版九年级上册21.2 二次函数的图象和性质课文配套课件ppt

这是一份初中数学沪科版九年级上册21.2 二次函数的图象和性质课文配套课件ppt，共50页。PPT课件主要包含了学习目标，数形结合直观感受，描点连线，yx2，观察图象回答问题串，在学中做在做中学，y-x2，我思我进步，对称轴的右，对称轴的左等内容，欢迎下载使用。

1.会用描点法画二次函数y=x2和y=-x2的图象。
2.根据函数y=x2和y=-x2的图象，直观地了解它的性质。
4.经历确定二次函数表达式的过程，体会求二次函数表达式的思想方法，培养数学应用意识。5.会利用待定系数法求二次函数的表达式。6.灵活应用二次函数的三种形式：一般式、顶点式、交点式，以便在用待定系数法求解二次函数表达式时减少未知数的个数，简化运算过程。
你想直观地了解它的性质吗？
在二次函数y=x2中，y随x的变化而变化的规律是什么？
观察y=x2的表达式，选择适当x值，并计算相应的y值，完成下表：
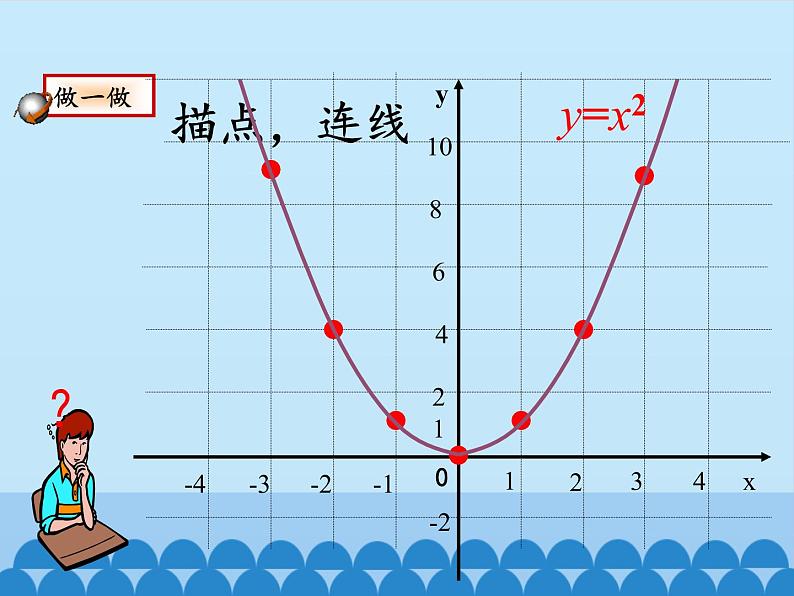
你会用描点法画二次函数y=x2的图象吗？
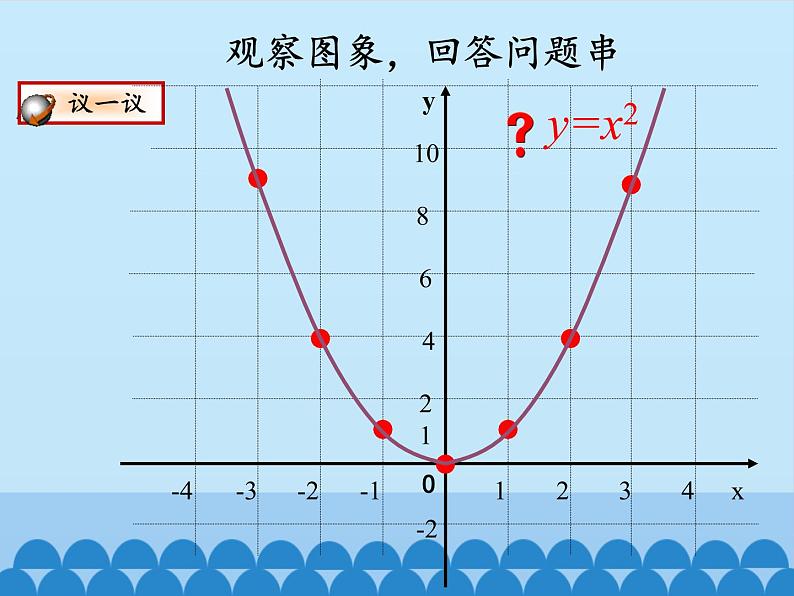
(1)你能描述图象的形状吗？与同伴进行交流。
(2)图象是轴对称图形吗？如果是，它的对称轴是什么？请你找出几对对称点，并与同伴交流。
(3)图象与x轴有交点吗？如果有，交点坐标是什么？
(4)当x<0时，随着x的值增大，y的值如何变化？当x>0呢？
(5)当x取什么值时，y的值最小？最小值是什么？你是如何知道的？
二次函数y=x2的图象形如物体抛射时所经过的路线，我们把它叫做抛物线。.
这条抛物线关于y轴对称，y轴就是它的对称轴。
对称轴与抛物线的交点叫做抛物线的顶点。
当x<0(在对称轴的左侧)时，y随着x的增大而减小。
当x>0(在对称轴的右侧)时，y随着x的增大而增大。
抛物线y=x2在x轴的上方(除顶点外)，顶点是它的最低点，开口向上，并且向上无限伸展;当x=0时，函数y的值最小，最小值是0。
(1)二次函数y=-x2的图象是什么形状？
你能根据表格中的数据作猜想吗？
(2)先想一想，然后作出它的图象。
(3)它与二次函数y=x2的图象有什么关系？
(2)图象与x轴有交点吗？如果有，交点坐标是什么？
(3)当x<0时，随着x的值增大，y的值如何变化？当x>0呢？
(4)当x取什么值时，y的值最小？最小值是什么？你是如何知道的？
(5)图象是轴对称图形吗？如果是，它的对称轴是什么？请你找出几对对称点，并与同伴交流。
二次函数y=-x2的图象形如物体抛射时所经过的路线，我们把它叫做抛物线。
当x<0(在对称轴的左侧)时，y随着x的增大而增大。
当x>0(在对称轴的右侧)时，y随着x的增大而减小。
抛物线y=-x2在x轴的下方(除顶点外)，顶点是它的最高点，开口向下，并且向下无限伸展;当x=0时，函数y的值最大，最大值是0。
函数y=ax2(a≠0)的图象和性质:
二次函数y=ax2的性质:
在x轴的上方（除顶点外）
在x轴的下方（除顶点外）
当x=0时，最小值为0
当x=0时，最大值为0
在对称轴的左侧，y随着x的增大而减小。在对称轴的右侧，y随着x的增大而增大。
在对称轴的左侧，y随着x的增大而增大。在对称轴的右侧，y随着x的增大而减小。
y=x2和y=-x2是y=ax2当a=±1时的特殊例子。a的符号确定着抛物线的……
在同一坐标系中作出函数y=x2和y=-x2的图象。
1.抛物线y=ax2的顶点是原点，对称轴是y轴。
2.当a>0时，抛物线y=ax2在x轴的上方(除顶点外)，它的开口向上，并且向上无限伸展；当a<0时，抛物线y=ax2在x轴的下方(除顶点外)，它的开口向下，并且向下无限伸展。
3.当a>0时，在对称轴的左侧，y随着x的增大而减小；在对称轴右侧，y随着x的增大而增大。当x=0时，函数y的值最小。当a<0时，在对称轴的左侧，y随着x的增大而增大；在对称轴的右侧，y随着x增大而减小。当x=0时，函数y的值最大。
二次函数y=ax2的性质
1.已知抛物线y=ax2经过点(-2，-8)。（1）求此抛物线的函数表达式；（2）判断点B(-1，-4)是否在此抛物线上；（3）求出此抛物线上纵坐标为-6的点的坐标。
解：(1)把(-2，-8)代入y=ax2，得-8=a(-2)2，解得a=-2，所求函数表达式为y=-2x2。
2.填空:(1)抛物线y=2x2的顶点坐标是 ，对称轴是 ，在 侧，y随着x的增大而增大；在 侧，y随着x的增大而减小，当x= 时，函数y的值最小，最小值是 ，抛物线y=2x2在x轴的 方(除顶点外)。
(2)抛物线 在x轴的 方(除顶点外)，在对称轴的左侧，y随着x的 ；在对称轴的右侧，y随着x的 ，当x=0时，函数y的值最大，最大值是 ，当x 0时，y<0。
2.当a>0时，抛物线y=ax2在x轴的上方（除顶点外），它的开口向上，并且向上无限伸展；当a<0时，抛物线y=ax2在x轴的下方（除顶点外），它的开口向下，并且向下无限伸展。
由二次函数y=x2和y=-x2知：
接下来，利用图象的对称性列表（请填表）
因此，抛物线 的对称轴是 ，顶点坐标是
一般地，我们可以用配方求抛物线y=ax2+bx+c(a≠0)的顶点与对称轴。
这是确定抛物线顶点与对称轴的公式。
矩形场地的周长是60m，一边长为l，则另一边长为 ，场地的面积
用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长l的变化而变化，当l是多少时，场地的面积S最大？
可以看出，这个函数的图象是一条抛物线的一部分，这条抛物线的顶点是函数的图象的最高点，也就是说，当l取顶点的横坐标时，这个函数有最大值。由公式可求出顶点的横坐标。
分析：先写出S与l的函数关系式，再求出使S最大的l值。
也就是说，当l是15m时，场地的面积S最大(S=225m2)。
因此，当 时，
例1 若二次函数图象过A(2，-4)，B(0，2)，C(-1，2)三点，求此函数的解析式。
例2 已知一个二次函数的图象经过点(4，-3)，并且当x=3时有最大值4，试确定这个二次函数的解析式。
解法2：（利用顶点式）∵当x=3时，有最大值4∴顶点坐标为(3，4)设二次函数解析式为：y=a(x-3)2+4∵函数图象过点(4，-3)∴a(4-3)2+4=-3∴a=-7∴二次函数的解析式为y=-7(x-3)2+4
例3 二次函数y=ax2+bx+c的图象过点A(0，5)，B(5，0)两点，它的对称轴为直线x=3，求这个二次函数的解析式。
小结: 已知顶点坐标(h，k)或对称轴方程x=h时优先选用顶点式。
解：（交点式）∵二次函数图象经过点(3，0)，(-1，0)∴设二次函数表达式为y=a(x-3)(x+1)∵函数图象过点(1，4)∴4=a(1-3)(1+1)，得a=-1∴函数的表达式为：y=-(x+1)(x-3)=-x2+2x+3
例4 已知二次函数图象经过(1，4)，(-1，0)和(3，0)三点，求二次函数的表达式。
知道抛物线与x轴的两个交点的坐标，选用交点式比较简便。
其它解法：（一般式）设二次函数解析式为y=ax2+bx+c∵二次函数图象过点(1，4)，(-1，0)和(3，0)解得∴函数的解析式为y=-x2+2x+3
（顶点式）解：∵抛物线与x轴相交两点(-1，0)和(3，0)∴(-1+3)/2=1∴点(1，4)为抛物线的顶点可设二次函数解析式为y=a(x-1)2+4∵抛物线过点(-1，0)∴0=a(-1-1)2+4，得a=-1∴函数的解析式为y=-(x-1)2+4
通过上述问题的解决，您能体会到求二次函数表达式采用的一般方法是什么？
你能否总结出上述解题的一般步骤？
1.若无坐标系，首先应建立适当的直角坐标系;2.设抛物线的表达式;3.写出相关点的坐标;4.列方程(或方程组);5.解方程或方程组，求待定系数;6.写出函数的表达式。
归纳：在确定二次函数的表达式时：（1）若已知图像上三个非特殊点，常设一般式；（2）若已知二次函数顶点坐标或对称轴，常设顶点式较为简便；（3）若已知二次函数与x轴的两个交点，常设交点式较为简单。
1．说说自己生活中遇到的哪些动物和植物身体的部分轮廓线呈抛物线形状。
2．设正方形的边长为a，面积为S，试作出S随a的变化而变化的图象。
3．写出下列抛物线的开口方向、对称轴及顶点坐标。当x为何值时，y的值最小（大）？
解:(1)a=3>0，抛物线开口向上
解:a=-1<0，抛物线开口向下
解:a=-2<0，抛物线开口向下
解:a=0.5>0，抛物线开口向上
4．已知直角三角形两条直角边的和等于8，两条直角边各为多少时，这个直角三角形的面积最大，最大值是多少？