初中数学人教版八年级上册13.4课题学习 最短路径问题精练

第13章轴对称13.4课题学习最短路径问题（选择题专练）

学校:___________姓名：___________班级：___________考号：___________

1．某开发商的经适房的三个居民小区A、B、C在同一条直线上，位置如图所示．其中小区B到小区A、C的距离分别是70m和150m，现在想在小区A、C之间建立一个超市，要求各小区居民到超市总路程的和最小，那么超市的位置应建在（　　）

A．小区A B．小区B C．小区C D．AC的中点

【答案】B

【解析】

【分析】

设超市为点P，则所求距离和为AP+BP+CP，再由AP+CP＝AC，则当点B与P重合时，AP+BP+CP＝AC此时距离和最小．

【详解】

解：设超市为点P，

∵P点在A、C 之间，

∴AP+BP+CP是超市到小区居民总路程的和，

∵AP+CP＝AC，

∴当PB最短时，即P点与B点重合时，AP+BP+CP＝AC，此时市到小区居民总路程的和最小，

故选：B．

【点评】

本题考查两点间的距离;熟练掌握线段上两点间的距离的求法，利用两点间线段最短解题是关键．

2．如图，直线m表示一条河，M，N表示两个村庄，欲在m上的某处修建一个给水站，向两个村庄供水，现有如图所示的四种铺设管道的方案，图中实线表示铺设的管道，则所需管道最短的方案是（    ）

A． B．

C． D．

【答案】D

【解析】

【分析】

本题可通过找点M或点N关于直线m的对称点，继而利用两点之间线段最短确定最短路径．

【详解】

作点M关于直线m的对称点，连接交直线m于P，则P处即为给水站位置．根据“两点之间，线段最短”可排除、、选项，可知选项管道最短．

故选：．

【点评】

本题考查将军饮马模型，可利用轴对称性质以及两点之间线段最短求解，将军饮马模型有诸多变体形式，需做专题训练对比记忆最佳．

3．为解决村庄灌溉问题，政府投资由水库向A，B，C，D这四个村庄铺设管道，现已知这四个村庄与水库以及村与村之间的距离(单位：km)如图所示，则把水库的水输送到这四个村庄铺设管道的总长度最短应是(　　)

A．16km B．17km C．18km D．20km

【答案】A

【解析】

【分析】

尽量选择数据较小的路线，到达4个村庄即可．

【详解】

最短总长度应该是：水库到A，再从A到B、D，然后从D到C，总长度为：4+5+3+4=16（km）．

故选A．

【点评】

找到最短路线是解决本题的关键．

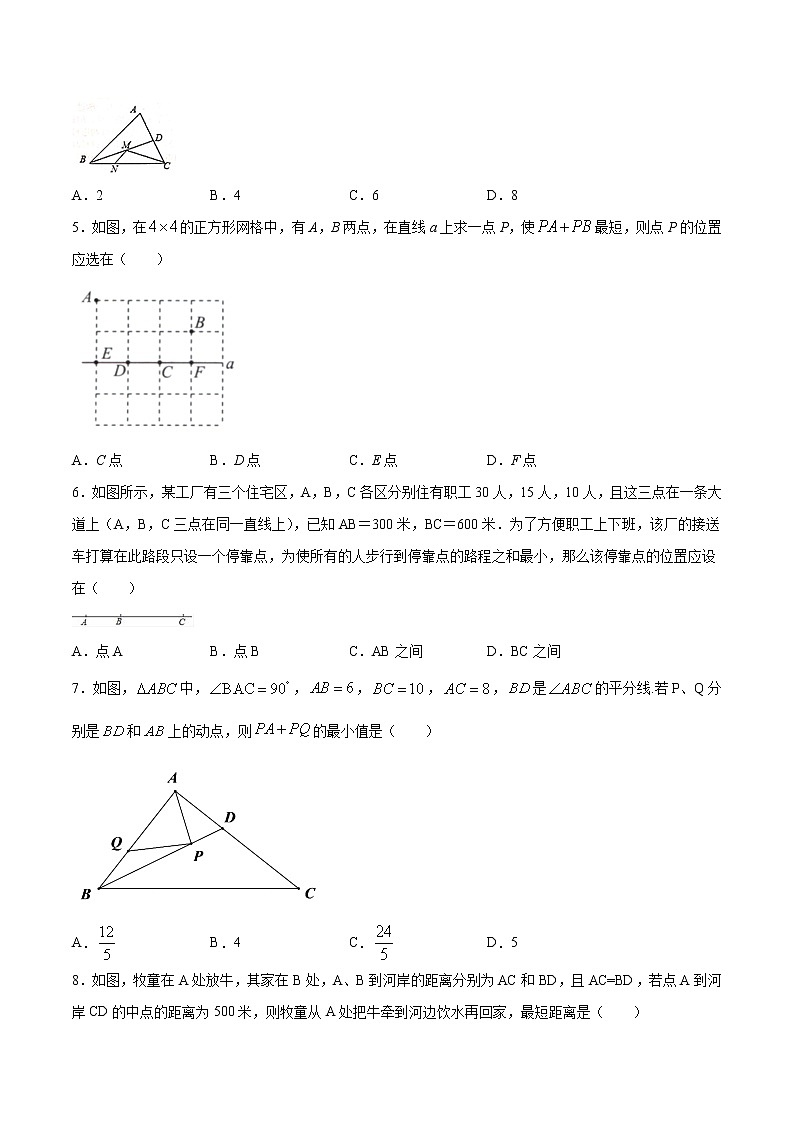
4．如图，在锐角三角形ABC中，AB=4，△ABC的面积为8，BD平分∠ABC．若M、N分别是BD、BC上的动点，则CM+MN的最小值是（   ）

A．2 B．4 C．6 D．8

【答案】B

【解析】

【分析】

过点C作CE⊥AB于点E，交BD于点M′，过点M′作M′N′⊥BC于N′，则CE即为CM+MN的最小值，再根据三角形的面积公式求出CE的长，即为CM+MN的最小值．

【详解】

解：过点C作CE⊥AB于点E，交BD于点M′，过点M作MN′⊥BC于N′，

∵BD平分∠ABC，M′E⊥AB于点E，M′N′⊥BC于N
∴M′N′=M′E，
∴CE=CM′+M′E
∴当点M与M′重合，点N与N′重合时，CM+MN的最小值．
∵三角形ABC的面积为8，AB=4，
∴×4•CE=8，
∴CE=4．
即CM+MN的最小值为4．
故选B．

【点评】

本题考查是轴对称-最短路线问题，根据题意作出辅助线，构造出三角形，利用三角形的面积求解是解题关键．

5．如图，在的正方形网格中，有A，B两点，在直线a上求一点P，使最短，则点P的位置应选在（    ）

A．C点 B．D点 C．E点 D．F点

【答案】A

【解析】

【分析】

首先求得点A关于直线a的对称点A′，连接A′B，即可求得答案．

【详解】

如图，

点是点A关于直线a的对称点，连接，则与直线a的交点即为点P，此时最短．

∵与直线a交于点C，

∴点P的位置应选在C点．

故选：A．

【点评】

本题考查了轴对称的性质，最短路径问题．注意首先作出其中一点关于直线a的对称点，对称点与另一点的连线与直线a的交点就是所要找的点．

6．如图所示，某工厂有三个住宅区，A，B，C各区分别住有职工30人，15人，10人，且这三点在一条大道上（A，B，C三点在同一直线上），已知AB＝300米，BC＝600米．为了方便职工上下班，该厂的接送车打算在此路段只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（　　）

A．点A B．点B C．AB之间 D．BC之间

【答案】A

【解析】

【分析】

此题为数学知识的应用，由题意设一个停靠点，为使所有的人步行到停靠点的路程之和最小，肯定要尽量缩短两地之间的里程，就用到两点间线段最短定理．

【详解】

解：①以点A为停靠点，则所有人的路程的和=15×300+10×900=13500（米），

②以点B为停靠点，则所有人的路程的和=30×300+10×600=15000（米），

③以点C为停靠点，则所有人的路程的和=30×900+15×600=36000（米），

④当在AB之间停靠时，设停靠点到A的距离是m，则（0＜m＜300），则所有人的路程的和是：30m+15（300-m）+10（900-m）=13500+5m＞13500，

⑤当在BC之间停靠时，设停靠点到B的距离为n，则（0＜n＜600），则总路程为30（300+n）+15n+10（600-n）=15000+35n＞13500．

∴该停靠点的位置应设在点A；

故选：A．

【点评】

考查了比较线段的长短，此题为数学知识的应用，考查知识点为两点之间线段最短．

7．如图，中，，，，，是的平分线.若P、Q分别是和上的动点，则的最小值是（    ）

A． B．4 C． D．5

【答案】C

【解析】

【分析】

在BC上截取，连接，易证，显然当A、P、三点共线且时，的值最小，问题转化为求△ABC中BC边上的高，再利用面积法求解即可.

【详解】

解：在BC上截取，连接，如图，

∵是的平分线，∴∠ABD=∠CBD，

在△PBQ和中，

∴△△PBQ≌（SAS），

∴，

∴，

∴当A、P、三点共线且时，的值最小，

过点A作AF⊥BC于点F，则的最小值即为AF的长，

∵，

∴，

即的最小值为.

故选C.

【点评】

本题考查了全等三角形的判定和性质、角平分线的定义、垂线段最短和面积法求高等知识，属于常考题型，在BC上截取，连接，构造全等三角形、把所求问题转化为求的最小值是解题的关键.

8．如图，牧童在A处放牛，其家在B处，A、B到河岸的距离分别为AC和BD，且AC=BD，若点A到河岸CD的中点的距离为500米，则牧童从A处把牛牵到河边饮水再回家，最短距离是（　　）

A．750米 B．1000米 C．1500米 D．2000米

【答案】B

【解析】

作A的对称点A’,连接A’B交CD于P,

,

,,

两点之间直线最短，A’B=AP+PB=1000米

点评：平面上最短路径问题

（1）归于“两点之间的连线中，线段最短”。凡属于求“变动的两线段之和的最小值”时，大都应用这一模型。

（2）归于“三角形两边之差小于第三边”。凡属于求“变动的两线段之差的最大值”时，大都应用这一模型。

（3）平面图形中，直线同侧两点到直线上一点距离之和最短问题。

9．A，B，C三个车站在东西方向笔直的一条公路上，现要建一个加油站使其到三个车站的距离和最小，则加油站应建在(　　)

A．在A的左侧 B．在AB之间 C．在BC之间 D．B处

【答案】D

【解析】

【分析】

设P、B的距离为xkm，根据线段的和差，可得加油站到三个车站的距离和为（AC+x）km，那么x为0，有最小距离和，依此即可求解．

【详解】

设P、B的距离为xkm，

如图1：

路程之和为PA+PC+PB=（AC+x）km；

如图2：

路程之和为PA+PC+PB=（AC+x）km；

综上所述：路程之和为=（AC+x）km，

当x=0时，路程之和为AC的长度，则加油站应建在B处．

故选D

【点评】

本题考查了直线、射线、线段，两点间的距离，读懂题意，找到所求量的等量关系是解决本题的关键．

10．A、B是直线l上的两点，P是直线l上的任意一点，要使PA+PB的值最小，那么点P的位置应在（　　）

A．线段AB上    B．线段AB的延长线上

C．线段AB的反向延长线上    D．直线l上

【答案】A

【解析】分类讨论：当P点在线段AB的延长线上，则PA＋PB＝AB＋2PB；当P点在线段AB的反向延长线上，则PA＋PB＝AB＋2PA；当P点在线段AB上，则PA＋PB＝AB，然后比较线段的大小即可得到结论．

详解：当P点在线段AB的延长线上，则PA＋PB＝PB＋AB＋PB＝AB＋2PB；

当P点在线段AB的反向延长线上，则PA＋PB＝PA＋AB＋PB＝AB＋2PA；

当P点在线段AB上，则PA＋PB＝AB，

所以当P点在线段AB上时PA＋PB的值最小．

故选：A．

点评：本题考查了比较线段的长短：比较两条线段长短的方法有两种：度量比较法、重合比较法．

11．如图是放在地面上的一个长方体盒子，其中，在线段的三等分点（E=3）处有一只蚂蚁，中点处有一米粒，则蚂蚁沿长方体表面爬到米粒处的最短距离为（  ）

A．10

B．

C．5+

D．6+

【答案】A

【解析】

【分析】

利用平面展开图有两种情况，画出图形利用勾股定理求出EF的长即可．

【详解】

如图1，

∵AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒，

∴BE=6，BF=5+3=8，

∴EF= =10；

如图2,∵AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁，

B′C′中点F处有一米粒，

∴BE=6，EN=9，FN=5，

∴EF= .

∵10<，

∴蚂蚁沿长方体表面爬到米粒处的最短距离为10.

故选A.

【点评】

此题考查平面展开-最短路径问题，解题关键在于解题关键在于画出图形.

12．如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，点B为劣弧AN的中点，点P是直径MN上的一动点，则PA＋PB的最小值为(    )

A． B．1 C．2 D．2

【答案】A

【解析】

【分析】

作点B关于MN的对称点B′，连接OA、OB、OB′、AB′，根据轴对称确定最短路线问题可得AB′与MN的交点即为PA+PB的最小时的点，根据在同圆或等圆中，同弧所对的圆心角等于圆周角的2倍求出∠AON＝60°，然后求出∠BON＝30°，再根据对称性可得∠B′ON＝∠BON＝30°，然后求出∠AOB′＝90°，从而判断出△AOB′是等腰直角三角形，再根据等腰直角三角形的性质可得AB′OA，即为PA+PB的最小值．

【详解】

作点B关于MN的对称点B′，连接OA、OB、OB′、AB′，则AB′与MN的交点即为PA+PB的最小时的点，PA+PB的最小值＝AB′．

∵∠AMN＝30°，∴∠AON＝2∠AMN＝2×30°＝60°．

∵点B为劣弧AN的中点，∴∠BON∠AON60°＝30°，由对称性，∠B′ON＝∠BON＝30°，∴∠AOB′＝∠AON+∠B′ON＝60°+30°＝90°，∴△AOB′是等腰直角三角形，∴AB′OA，即PA+PB的最小值．

故选A．

【点评】

本题考查了轴对称确定最短路线问题，在同圆或等圆中，同弧所对的圆心角等于圆周角的2倍的性质，作辅助线并得到△AOB′是等腰直角三角形是解题的关键．

13．如图，把矩形ABCD沿对角线BD折叠，重叠部分为△EBD，则下列说法可能错误的是(　　)

A．AB＝CD B．∠BAE＝∠DCE

C．EB＝ED D．∠ABE=30°

【答案】D

【解析】

【分析】

根据ABCD为矩形，所以∠BAE=∠DCE，AB=CD，再由对顶角相等可得∠AEB=∠CED，所以△AEB≌△CED，就可以得出BE=DE，由此判断即可．

【详解】

∵四边形ABCD为矩形

∴∠BAE=∠DCE，AB=CD，故A. B选项正确；

在△AEB和△CED中，

，

∴△AEB≌△CED(AAS)，

∴BE=DE，故C正确；

∵得不出∠ABE=∠EBD，

∴∠ABE不一定等于30°，故D错误.

故选：D.

【点评】

此题考查翻折变换（折叠问题），解题关键在于利用全等三角形的性质进行解答.

14．如图，△ABC中，AB=AC，BC=5，，于D，EF垂直平分AB，交AC于F，在EF上确定一点P使最小，则这个最小值为（   ）

A．3 B．4 C．5 D．6

【答案】D

【解析】

【分析】

根据三角形的面积公式得到AD=6，由EF垂直平分AB，得到点A，B关于执行EF对称，于是得到AD的长度=PB+PD的最小值，即可得到结论．

【详解】

∴AD=6，

∵EF垂直平分AB，

∴点A，B关于直线EF对称，

∴AD的长度=PB+PD的最小值，

即PB+PD的最小值为6，

故答案选D.

【点评】

本题考查的知识点是线段垂直平分线的性质及等腰三角形的性质以及轴对称-最短路线问题，解题的关键是熟练的掌握线段垂直平分线的性质及等腰三角形的性质以及轴对称-最短路线问题.

15．如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（ ）

A．①② B．②③ C．①③ D．①④

【答案】D

【解析】

试题解析：∵AE=AB，

∴BE=2AE，

由翻折的性质得，PE=BE，

∴∠APE=30°，

∴∠AEP=90°﹣30°=60°，

∴∠BEF=（180°﹣∠AEP）=（180°﹣60°）=60°，

∴∠EFB=90°﹣60°=30°，

∴EF=2BE，故①正确；

∵BE=PE，

∴EF=2PE，

∵EF＞PF，

∴PF＜2PE，故②错误；

由翻折可知EF⊥PB，

∴∠EBQ=∠EFB=30°，

∴BE=2EQ，EF=2BE，

∴FQ=3EQ，故③错误；

由翻折的性质，∠EFB=∠EFP=30°，

∴∠BFP=30°+30°=60°，

∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°，

∴∠PBF=∠PFB=60°，

∴△PBF是等边三角形，故④正确；

综上所述，结论正确的是①④．

故选D．

考点：1．翻折变换（折叠问题）；2．矩形的性质．