





- 人教版数学八上 13.3.4 等边三角形 课件 课件 15 次下载
- 人教版数学八上 13.3.5 等边三角形 课件 课件 15 次下载
- 人教版数学八上 13.4.2 最短路径问题 课件 课件 14 次下载
- 人教版数学八上 第十三章轴对称 小结复习1 课件 课件 15 次下载
- 人教版数学八上 第十三章轴对称 小结复习2 课件 课件 14 次下载
初中数学人教版八年级上册13.4课题学习 最短路径问题精品课件ppt
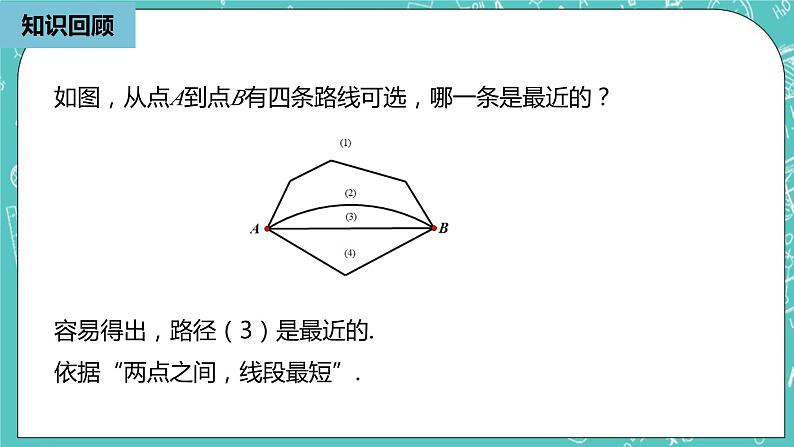
展开如图,从点A到点B有四条路线可选,哪一条是最近的?
容易得出,路径(3)是最近的.依据“两点之间,线段最短”.
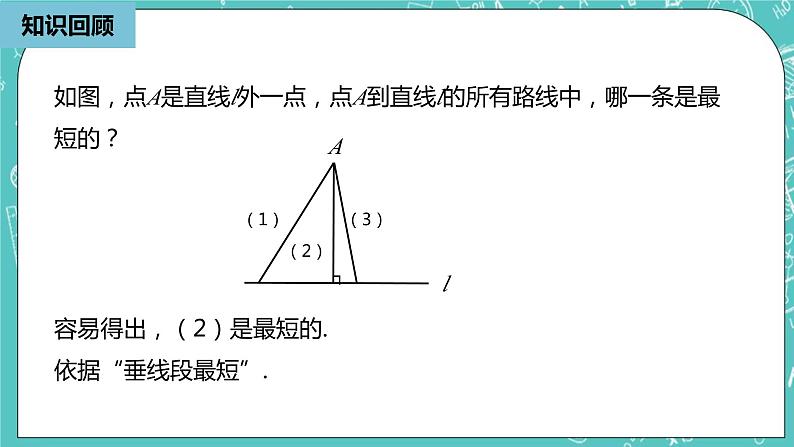
如图,点A是直线l外一点,点A到直线l的所有路线中,哪一条是最短的?
容易得出,(2)是最短的.依据“垂线段最短”.
如图,直线l是线段AB的垂直平分线,点C是直线l上任意一点,则AC和BC的大小关系是什么?
容易得出,AC=BC.依据“线段垂直平分线上的点到线段两端点的距离相等”.
1、利用轴对称解决简单的最短路径问题.2、体会图形的变化在解决最值问题中的作用,感受由实际问题转化为数学问题的思想.
思考:相传古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图1中的A地出发,到一条笔直的河边l饮马,然后到B地.到河边什么地方饮马可使他所走的路线全程最短?精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马问题”.
这是个实际问题,你能用自己理解的语言描述一下吗?
如图所示:将A,B 两地抽象为两个点,将河l抽象为一条直线.
那你能用数学语言说明这个问题所表达的意思吗?
如图: 点A,B分别在直线l的同侧,点C是直线l上的一个动点,当点C在什么位置的时候,AC+BC的值最小?
如果点A,B在直线l的两侧,这时该如何求解?
解析:连接A,B两点,交直线l于点C,则点C即为所求的位置,可以使得AC+BC的值最小.依据:两点之间,线段最短.
如图: 点A,B分别在直线l的两侧,点C是直线l上的一个动点,当点C在什么位置的时候,AC+BC的值最小?
你能利用两点分别在直线两侧的解题思路,来解决两点在直线同一侧的问题吗?
分析:如果我们能够把点B转移到直线l的另外一侧B′,同时使得对直线上任意一点C,满足BC=B′C,就可以将问题转化为“两点分别在直线两侧的情况”.那么在直线l上使得满足BC=B′C的点应该怎么找呢?
如图,作出点B关于直线l的对称点B′,利用轴对称的性质可知:对于直线l上的任意一点C均满足BC=B′C.此时,问题转化为:当点C在直线l的什么位置时,AB+B′C的值最小?
容易得出:连接AB′交直线l于点C,则点C即为所求.
证明:在直线l上任意取一点C′(不与点C重合),连接AC′,BC′,B′C′.由轴对称的性质可得:BC=B′C,BC′=B′C′,则AC+BC=AC+B′C=AB′,AC′+BC′=AC′+B′C′.在△AB′C′中,AB′
如图,点A,B分别是直线l异侧的两个点,在直线l上找一点C使得AC+BC的值最小,此时点C就是线段AB与直线l的交点.
2、直线同侧的两点到直线上一点距离和最短的问题.
如图,点A,B分别是直线l同侧的两个点,在直线l上找一点C使得AC+BC的值最小,这时先作点B关于直线l的对称点的B′,连接AB′交直线l于点C(也可以作点A关于直线l的对称点A′,连接A′B交直线l于点C),此时点C就是所求作的点.
如图,A,B两个小镇在河的同侧,现要在笔直的河边a上修建一个自来水厂分别向两个镇供水,如何选择自来水厂的位置,可使用的水管最短?
解:如图,作点B关于河边a的对称点B′,连接AB′交河边a于点P,则点P所在的位置为所求的自来水厂的位置.
如图,点A,B是直线l同侧不重合的两点,在直线l上求作一点C,使得AC+BC的长度最短.作法:①作点B关于直线l的对称点B′;②连接AB′,与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有用到的知识或方法是( )A.转化思想B.三角形两边之和大于第三边C.两点之间,线段最短D.三角形的一个外角大于与它不相邻的任意一个内角
如图,点A,B是直线l同侧不重合的两点,在直线l上求作一点C,使得AC+BC的长度最短.作法:①作点B关于直线l的对称点B′;②连接AB′,与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有用到的知识或方法是( )
分析:上述题目中应用了轴对称把最短路径问题转化为“两点之间,线段最短”来解决,该过程用到了“转化思想”,“两点之间,线段最短”,验证是否为最短距离时利用了三角形两边之和大于第三边.
两棵树的位置如图所示,树的底部分别为点A,B,有一只昆虫沿着A至B的路径在地面爬行,小树的树顶D处有一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小虫在AB之间何处被小鸟抓住时,小鸟飞行路程最短,在图中画出该点的位置.
解:如图,作点C关于AB的对称点C′,连接DC′交AB于点E,则点E即为所求.也可作点D关于AB的对称点D′,连接CD′同样交AB于点E的位置,则点E即为所求.
如图,在等腰Rt△ABC中,D是BC边的中点,E是AB边上的一动点,要使EC+ED最小,请找点E的位置.
分析:上述题目可以描述为,点C,D为线段AB同侧的两点,在线段AB上找到一点E使得CE+DE的值最小.
解:如图所示,作点D关于线段AB的对称点D′,连接CD′交线段AB于点E,则点E即为所求,也就是使得EC+ED最小的位置.
如图,牧童在A处放牛,家在B处,A,B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD中点距离为600,则牧童从A处把牛牵到河边饮水再回家,最短距离是( ) A.900 B.1200 C.1500 D.1800
分析:“牧童从A处把牛牵到河边饮水再回家,最短距离”可以转化为“点A,B均在河边CD的同侧,请在河边CD上找一点E,使得AE+BE的值最小”.
根据本节课所学的知识,点E比较容易找出,那AE+BE的值应该是多少呢?
解:延长AC至点A′,使得A′C=AC,连接A′B交CD于点E,连接AE.则点E即为所求的点.
分析:如图,A′C=AC=BD,AC⊥CD,BD⊥CD.猜测E是CD的中点,则AE=600,所以AE+BE=1200.
初中数学人教版八年级上册13.4课题学习 最短路径问题习题ppt课件: 这是一份初中数学人教版八年级上册13.4课题学习 最短路径问题习题ppt课件,共10页。
数学八年级上册13.4课题学习 最短路径问题试讲课教学课件ppt: 这是一份数学八年级上册13.4课题学习 最短路径问题试讲课教学课件ppt,共16页。PPT课件主要包含了将军饮马问题等内容,欢迎下载使用。
2021学年13.4课题学习 最短路径问题优质课课件ppt: 这是一份2021学年13.4课题学习 最短路径问题优质课课件ppt,文件包含134课程学习最短路径问题课件pptx、134课程学习最短路径问题教案doc、134课程学习最短路径问题练习doc等3份课件配套教学资源,其中PPT共30页, 欢迎下载使用。













