初二数学2022年江阴市敔山湾学校初二数学3月月考试题

这是一份初二数学2022年江阴市敔山湾学校初二数学3月月考试题，文件包含202203敔山湾初二数学02doc、202203敔山湾初二数学01docx等2份试卷配套教学资源，其中试卷共9页， 欢迎下载使用。

命题人：刘茜 审题人：苏晓飞
一、选择题（共10小题，每题3分, 共30分）
1．下列各图是选自历届世博会会徽中的图案．其中是中心对称图形的图案是( )
2．下列调查中，最适合采用普查方式的是( )
A．对无锡市初中学生每天阅读时间的调查 B．对端午节期间市场上粽子质量情况的调查
C．对某批次手机的防水功能的调查 D．对某校八年级（1）班学生肺活量情况的调查
3．将分式EQ \F(2m,m－n)中的m、n都扩大为原来的3倍，则分式的值( )
A．不变 B．扩大3倍 C．扩大6倍 D．扩大9倍
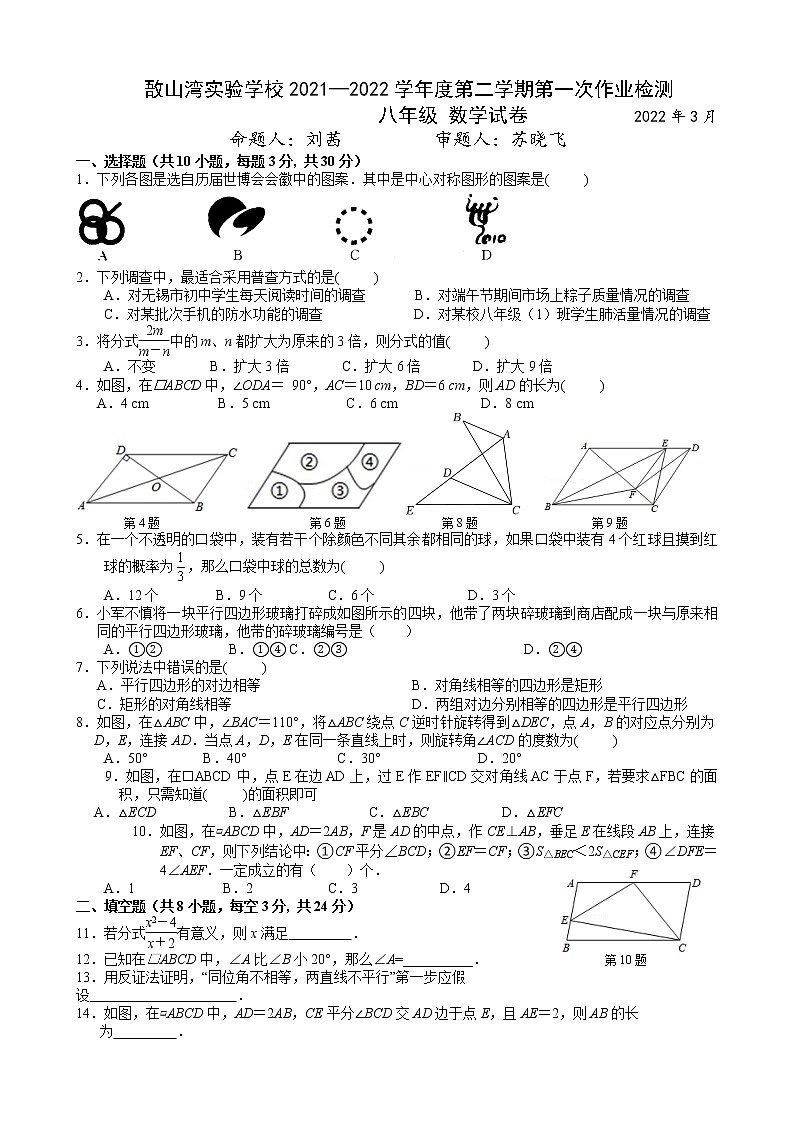
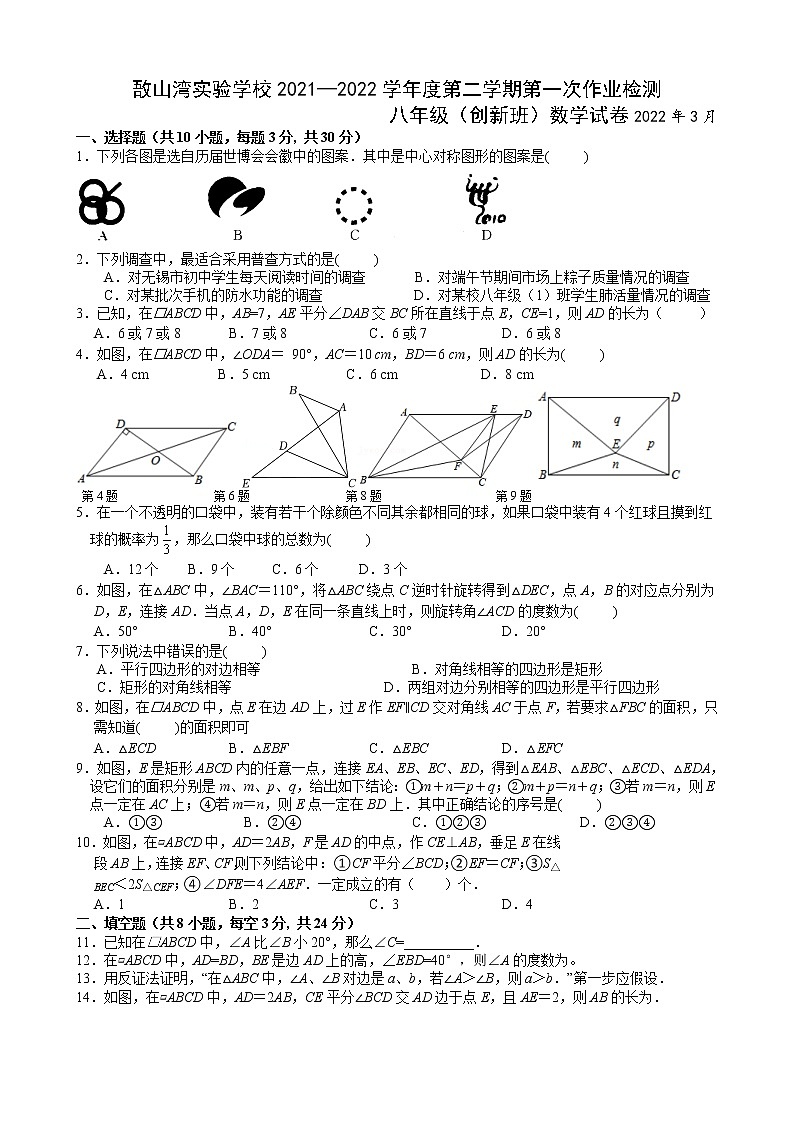
4．如图，在ABCD中，∠ODA＝ 90°，AC＝10 cm，BD＝6 cm，则AD的长为( )
A．4 cm B．5 cm C．6 cm D．8 cm

第4题 第6题 第8题 第9题
在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有4个红球且摸到红球的概率为，那么口袋中球的总数为( )
A．12个B．9个C．6个 D．3个
6．小军不慎将一块平行四边形玻璃打碎成如图所示的四块，他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃，他带的碎玻璃编号是（ ）
A．①② B．①④ C．②③ D．②④
7．下列说法中错误的是( )
A．平行四边形的对边相等 B．对角线相等的四边形是矩形
C．矩形的对角线相等 D．两组对边分别相等的四边形是平行四边形
8．如图，在△ABC中，∠BAC＝110°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，则旋转角∠ACD的度数为( )
A．50° B．40° C．30° D．20°
9．如图，在ABCD中，点E在边AD上，过E作EF∥CD交对角线AC于点F，若要求△FBC的面积，只需知道( )的面积即可
A．△ECDB．△EBFC．△EBCD．△EFC
第10题
10．如图，在▱ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中：①CF平分∠BCD；②EF＝CF；③S△BEC＜2S△CEF；④∠DFE＝4∠AEF．一定成立的有（ ）个．
A．1 B．2 C．3 D．4
二、填空题（共8小题，每空3分, 共24分）
11．若分式eq \f(x2－4,x＋2)有意义，则x满足 ．
12．已知在□ABCD中，∠A比∠B小20°，那么∠A=__________．
13．用反证法证明，“同位角不相等，两直线不平行”第一步应假设 ．
14．如图，在▱ABCD中，AD＝2AB，CE平分∠BCD交AD边于点E，且AE＝2，则AB的长为 ．
15．如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平，再一次折叠，使点D落在EF上G点处，并使折痕经过点A，展开纸片后∠DAG的大小为 ．
A
B
C
D
E
F
第14题 第15题 第16题 第17题
16．在平面直角坐标系中，□ABCD的边OC落在x轴的正半轴上，且点C (4，0)，B (6，2)，直线
第18题
y =kx + 4可将□ABCD的面积平分，则k＝ ．
17．如图，在△ABC中，AB＝2，AC＝ EQ \R(,2)，∠BAC＝105°，△ABD、△ACE、△BCF都是等边三角形，则四边形AEFD的面积为 ．
18．如图，在矩形ABCD中，E，F分别是边AB，AD上的动点，P是线段EF的中点，PG⊥BC，PH⊥CD，G，H为垂足，连接GH．若AB＝8，AD＝6，EF＝6，则GH的最小值是 ．
三、解答题（共66分）
19．（本题8分）计算：(1)－－+； （2）．
20．（本题6分）有一道题：先化简再求值：（eq \f(x－1,x+1) + eq \f(2x,x2－1)）÷eq \f(1,x2－1)，其中x＝，小明做题时把x＝错抄成了x＝，但他的计算结果也正确，请你通过计算解释这是为什么？
21．（本题7分）如图，在正方形网格中，每个小正方形的边长为1个单位长度．平面直角坐标系xOy的原点O在格点上，x轴、y轴都在格线上．线段AB的两个端点也在格点上．
（1）若将线段AB绕点O顺时针旋转90°得到线段A′B′．试在图中画出线段A′B′；
（2）若线段A″B″与线段A′B′关于y轴对称，请画出线段A″B″；
（3）若点P是此平面直角坐标系内的一点，当点A、B′、B″、P四边围成的四边形为平行四边形时，请你直接写出点P的坐标．
22．（本题8分）近年来，各市大力发展绿色交通，构建公共绿色交通体系，“共享单车”给人们的出行带来便利．小亮随机调查了若干市民租用共享单车的骑车时间单位：分，并将获得的数据分成四组，绘制了如下的统计图，请根据图中信息，解答下列问题：
（1）这次被调查的总人数是______．
（2）补全条形统计图；
（3）在扇形统计图中，求表示A组（t≤10分）的扇形圆心角的度数；
（4）如果骑共享单车的平均速度为12km/h，请估算，在租用共享单车的市民中，骑车路程不超过6km的人数所占的百分比．
23．（本题8分）如图，在四边形ABCD中，AD∥BC，对角线AC、BD交于点O，且AO＝OC，过点O作EF⊥BD，交AD于点E，交BC于点F．
（1）求证：四边形ABCD为平行四边形；
（2）连接BE，若∠BAD＝100°，∠DBF＝2∠ABE，求∠ABE的度数．
24．（本题8分）如图，在 ABCD 中，AC⊥BC，过点 D 作 DE∥AC 交 BC 的延长线于点 E，连接 AE 交 CD 于点 F．
（1）求证：四边形 ADEC 是矩形；
（2）在 ABCD 中，取 AB 的中点 M，连接 CM，若 CM=5，且 AC=8，求四边形 ADEC的面积．
25．（本题10分）如图，在平面直角坐标系中，长方形OABC的顶点A（6，0）、B（6，4），D是BC的中点，动点P从O点出发，以每秒1个单位的速度，沿着OA、AB、向终点B运动，设P点运动的时可为t秒（0＜t＜10）．
（1）当△POD的面积等于9时，点P的坐标为 ：
（2）当点P在OA上运动时，连接CP．问：是否存在某时刻t，当CP绕点P旋转时，点C能恰好落到AB的中点处？若存在，请求出t的值；若不存在，请说明理由．
（3）当t为何值时，点B关于直线PD的对称点恰好落在直线OP上．
26．（本题11分）在矩形ABCD中，AB＝6，BC＝4，以点A为旋转中心，逆时针旋转矩形ABCD，旋转角为α（0°＜α＜180°），得到矩形AEFG，点B、点C、点D的对应点分别为点E、点F、点G．
（1）如图①，当点E落在DC边上时，直写出线段EC的长度为 ；
（2）如图②，当点E落在线段CF上时，AE与DC相交于点H，连接AC，
①求证：△ACD≌△CAE；②求线段DH的长度．
（3）如图③设点P为边FG的中点，连接PB，PE，在矩形ABCD旋转过程中，△BEP的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．