初中数学人教版七年级下册5.2.1 平行线学案

这是一份初中数学人教版七年级下册5.2.1 平行线学案，共10页。
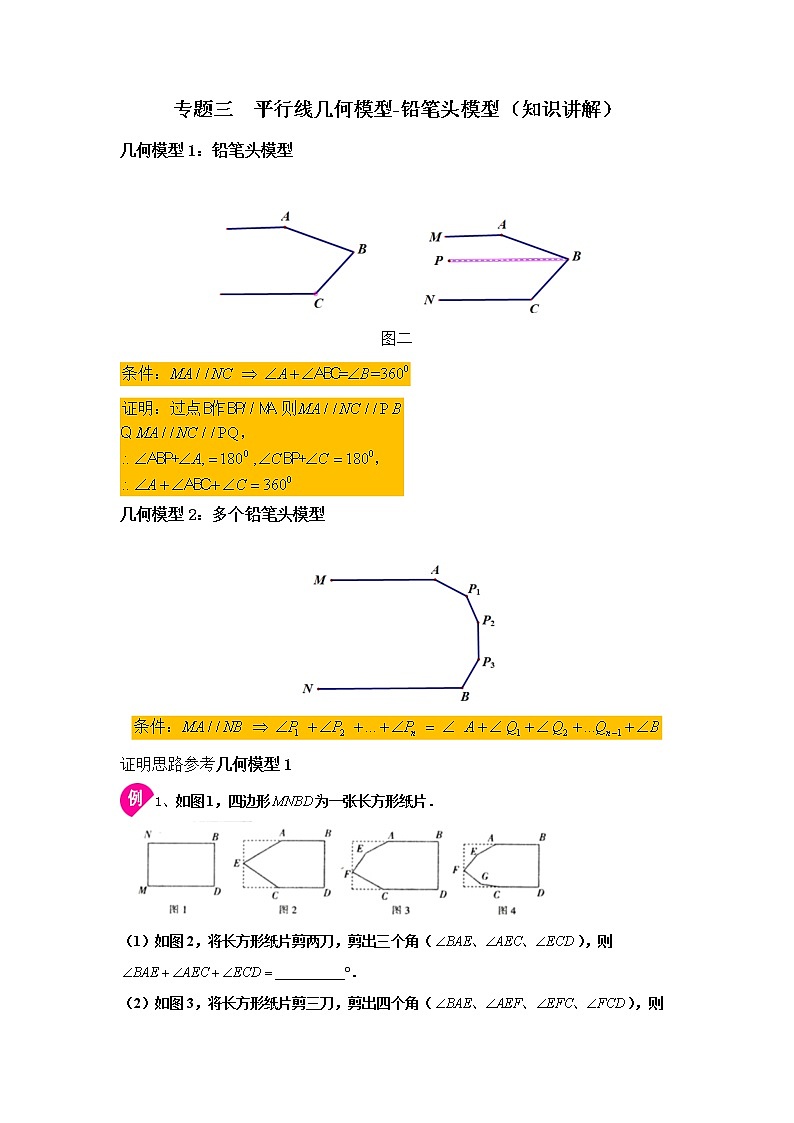
专题三  平行线几何模型-铅笔头模型（知识讲解）几何模型1：铅笔头模型       图二几何模型2：多个铅笔头模型 证明思路参考几何模型11、如图1，四边形为一张长方形纸片．（1）如图2，将长方形纸片剪两刀，剪出三个角（），则__________°．（2）如图3，将长方形纸片剪三刀，剪出四个角（），则__________°．（3）如图4，将长方形纸片剪四刀，剪出五个角（），则___________°．（4）根据前面探索出的规律，将本题按照上述剪法剪刀，剪出个角，那么这个角的和是____________°．【答案】（1）360；（2）540；（3）720；（4）．【分析】（1）过点E作EH∥AB，再根据两直线平行，同旁内角互补即可得到三个角的和等于180°的2倍；
（2）分别过E、F分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；
（3）分别过E、F、G分别作AB的平行线，根据两直线平行，同旁内角互补即可得到四个角的和等于180°的三倍；
（4）根据前三问个的剪法，剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．解：（1）过E作EH∥AB（如图②）．
∵原四边形是长方形，
∴AB∥CD，
又∵EH∥AB，
∴CD∥EH（平行于同一条直线的两条直线互相平行）．
∵EH∥AB，
∴∠A+∠1=180°（两直线平行，同旁内角互补）．
∵CD∥EH，
∴∠2+∠C=180°（两直线平行，同旁内角互补）．
∴∠A+∠1+∠2+∠C=360°，
又∵∠1+∠2=∠AEC，
∴∠BAE+∠AEC+∠ECD=360°；

（2）分别过E、F分别作AB的平行线，如图③所示，

用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°；
（3）分别过E、F、G分别作AB的平行线，如图④所示，

用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°；
（4）由此可得一般规律：剪n刀，剪出n+1个角，那么这n+1个角的和是180n度．
故答案为：（1）360；（2）540；（3）720；（4）180n．【点拨】本题主要考查了多边形的内角和，作平行线并利用两直线平行，同旁内角互补是解本题的关键，总结规律求解是本题的难点．2、如图，在六边形ABCDEF中，AF∥CD，A140，C165．（1）求B的度数；（2）当D    °时，AB∥DE？为什么？【答案】（1）°；（2）140°【分析】（1）过点B作BM∥AF，则BM∥AF∥CD，A140，C165，进而即可求解；（2）延长AB，DC交于点N，由∠ABC=55°，CD165,得∠C=40°，结合AB∥DE，即可得到答案．解：（1）过点B作BM∥AF，∵AF∥CD，∴BM∥AF∥CD，∴∠A+∠ABM=180°，∠C+∠CBM=180°，∵A140，C165，∴B=∠ABM+∠CBM=360°-∠A-∠C=360°-140-165°．（2）延长AB，DC交于点N，∵∠ABC=55°，∴∠NBC=125°，∵CD165,∴∠C165125°=40°若AB∥DE，则∠D=180°-40°=140°．故答案是：140° 【点拨】本题主要考查平行线的性质和三角形外角的性质，掌握两直线平行，同旁内角互补，是解题的关键．3、如图所示，，与的角平分线相较于点，，求的度数.【答案】.【分析】先设，，由题意的，，题意得到；由侧M图知，.解：设，，与的角平分线相交于点，，，由笔尖图知，，即，，由侧M图知，.【点拨】本题考查平行线的性质和角平分线，解题的关键是设，，并由题意得到x，y的关系式.4、问题情景：如图1，AB∥CD，∠PAB＝140°，∠PCD＝135°，求∠APC的度数．（1）丽丽同学看过图形后立即口答出：∠APC＝85°，请补全她的推理依据．如图2，过点P作PE∥AB，因为AB∥CD，所以PE∥CD．（      ）所以∠A+∠APE＝180°，∠C+∠CPE＝180°．（      ）因为∠PAB＝140°，∠PCD＝135°，所以∠APE＝40°，∠CPE＝45°，∠APC＝∠APE+∠CPE＝85°．问题迁移：（2）如图3，AD∥BC，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β，求∠CPD与∠α、∠β之间有什么数量关系？请说明理由．（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请直接写出∠CPD与∠α、∠β之间的数量关系． 【答案】（1）平行于同一条直线的两条直线平行（或平行公理推论），两直线平行，同旁内角互补；（2），理由见解析；（3）或【分析】（1）根据平行线的判定与性质填写即可；（2）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案；（3）画出图形（分两种情况①点P在BA的延长线上，②点P在AB的延长线上），根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案．解：（1）如图2，过点P作PE∥AB，因为AB∥CD，所以PE∥CD．（平行于同一条直线的两条直线平行）所以∠A+∠APE＝180°，∠C+∠CPE＝180°．（两直线平行同旁内角互补）因为∠PAB＝140°，∠PCD＝135°，所以∠APE＝40°，∠CPE＝45°，∠APC＝∠APE+∠CPE＝85°．故答案为：平行于同一条直线的两条直线平行；两直线平行，同旁内角互补；（2）∠CPD=∠α+∠β，理由如下：如图3所示，过P作PE∥AD交CD于E，
∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE+∠CPE=∠α+∠β；（3）当P在BA延长线时，如图4所示：
过P作PE∥AD交CD于E，同（2）可知：∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠β-∠α；当P在AB延长线时，如图5所示：
同（2）可知：∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠α-∠β．综上所述，∠CPD与∠α、∠β之间的数量关系为：∠CPD=∠β-∠α或∠CPD=∠α-∠β．【点拨】本题考查了平行线的性质和判定定理，正确作出辅助线是解答此题的关键．5、如图，已知AB∥CD，分别探究下面三个图形中∠P和∠A，∠C的关系，请你从所得三个关系中任意选出一个，说明你探究结论的正确性．结论：（1）___________________； （2）____________________；（3）_____________________；（4）选择结论____________，说明理由．【答案】（1）∠APC+∠PAB+∠PCD=360°；（2）∠APC=∠PAB+∠PCD；（3）∠PCD=∠APC+∠PAB；（4）∠APC+∠PAB+∠PCD=360°，理由见解析．【分析】（1）过点P作PE∥AB，则AB∥PE∥CD，再根据两直线平行，同旁内角互补即可解答；（2）过点P作PF∥AB，则AB∥CD∥PF，再根据两直线平行，内错角相等即可解答；（3）根据AB∥CD，可得出∠1=∠PCD，再根据三角形外角的性质进行解答；（4）选择以上结论任意一个进行证明即可．解：（1）过点P作PE∥AB，则AB∥PE∥CD，∴∠1+∠PAB=180°，∠2+∠PCD=180°，∴∠APC+∠PAB+∠PCD=360°．故答案为：∠APC+∠PAB+∠PCD=360°；（2）过点P作直线PF∥AB，∵AB∥CD，∴AB∥PF∥CD，∴∠PAB=∠1，∠PCD=∠2，∴∠APC=∠PAB+∠PCD．故答案为：∠APC=∠PAB+∠PCD；（3）∵AB∥CD，∴∠1=∠C，∵∠1=∠PAB+∠APC，∴∠PCD=∠APC+∠PAB．故答案为：∠PCD=∠APC+∠PAB．（4）选择结论∠APC+∠PAB+∠PCD=360°理由：过点P作PE∥AB，则AB∥PE∥CD，∴∠1+∠PAB=180°，∠2+∠PCD=180°，∴∠APC+∠PAB+∠PCD=360°故答案为：∠APC+∠PAB+∠PCD=360°．【点拨】本题考查的是平行线的性质及三角形外角的性质，能根据题意作出辅助线，再利用平行线的性质进行解答是解答此题的关键