初中冀教版第二十一章 一次函数综合与测试巩固练习

这是一份初中冀教版第二十一章 一次函数综合与测试巩固练习，共30页。试卷主要包含了一次函数的大致图象是，已知一次函数y=kx+b，若直线y＝kx＋b经过一，已知正比例函数的图像经过点等内容，欢迎下载使用。

八年级数学下册第二十一章一次函数专题练习
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，在平面直角坐标系中，，，，点D在线段BA上，点E在线段BA的延长线上，并且满足，M为线段AC上一点，当点D、M、E构成以M为直角顶点的等腰直角三角形时，M点坐标为（ ）

A． B． C． D．
2、若点(－3，y1)、(2，y2)都在函数y＝－4x＋b的图像上，则y1与y2的大小关系（ ）
A．y1＞y2 B．y1＜y2 C．y1＝y2 D．无法确定
3、甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．

则下列结论：
①A，B两城相距300千米；
②乙车比甲车晚出发1小时，却早到1小时；
③乙车出发后2.5小时追上甲车；
④当甲、乙两车相距50千米时，或．
其中正确的结论有（ ）
A．1个 B．2个 C．3个 D．4个
4、一次函数的大致图象是（ ）
A． B．
C． D．
5、已知点，在一次函数的图像上，则m与n的大小关系是（ ）
A． B． C． D．无法确定
6、已知一次函数y=kx+b（k，b为常数，且k≠0）的图象经过点（0，-1），且y的值随x值的增大而增大，则这个一次函数的表达式可能是（　　）
A．y＝﹣2x+1 B．y＝2x+1 C．y＝﹣2x﹣1 D．y＝2x﹣1
7、若直线y＝kx＋b经过一、二、四象限，则直线y＝bx﹣k的图象只能是图中的（ ）
A． B． C． D．
8、已知正比例函数的图像经过点（2，4）、（1，）、（1，），那么与的大小关系是（ ）
A． B． C． D．无法确定
9、在平面直角坐标系中，若函数的图象经过第一、二、三象限，则的取值（ ）
A．小于0 B．等于0 C．大于0 D．非负数
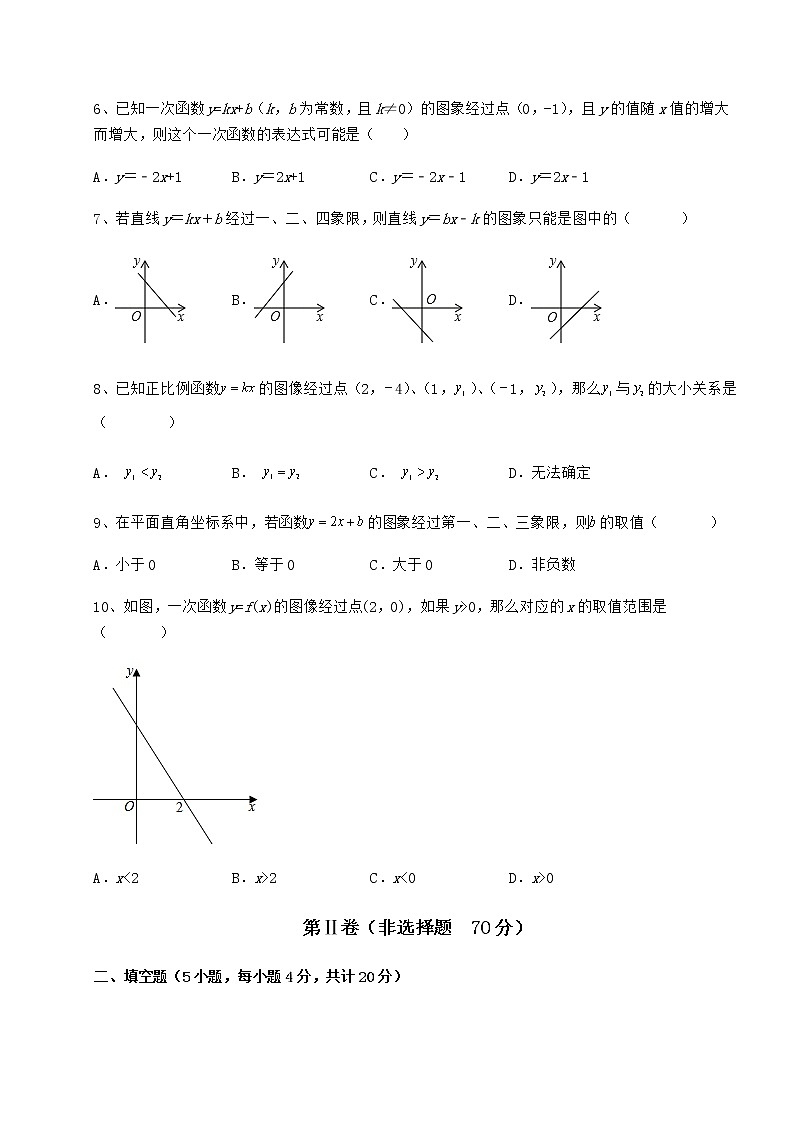
10、如图，一次函数y=f(x)的图像经过点(2，0)，如果y>0，那么对应的x的取值范围是（ ）

A．x<2 B．x>2 C．x<0 D．x>0
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、在运用一次函数解决实际问题时，首先判断问题中的两个变量之间是不是____关系，当确定是一次函数关系时，可求出函数解析式，并运用一次函数的图象和性质进一步求得我们所需要的结果．
2、如图，直线l1：y＝kx＋b与直线l2：y＝﹣x＋4相交于点P，若点P（1，n），则方程组的解是_____．

3、如图，一次函数x+4的图像与x轴交于点A，与y轴交于点B，C是x轴上的一动点，连接BC，将沿BC所在的直线折叠，当点A落在y轴上时，点C的坐标为_____．

4、一次函数y＝（k﹣1）x＋3中，函数值y随x的增大而减小，则k的取值范围是_____．
5、已知 M（1， a ）和 N（2， b ）是一次函数 y＝－x＋1 图像上的两点，则 a______b （填“＞”、“＜”或“＝”）．
三、解答题（5小题，每小题10分，共计50分）
1、为巩固拓展脱贫攻坚成果，开启乡村振兴发展之门，某村村民组长组织村民加工板栗并进行销售．根据现有的原材料，预计加工规格相同的普通板栗、精品板栗共4000件．某天上午的销售件数和所卖金额统计如下表：

普通板栗（件）
精品板栗（件）
总金额（元）
甲购买情况
2
3
350
乙购买情况
4
1
300
(1)求普通板栗和精品板栗的单价分别是多少元．
(2)根据（1）中求出的单价，若普通板栗和精品板栗每件的成本分别为40元、60元，且加工普通板栗a件（），则4000件板栗的销售总利润为w元．问普通板栗和精品板栗各加工多少件，所获总利润最多？最多总利润是多少？
2、如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．
（1）求对角线AB所在直线的函数关系式；
（2）对角线AB的垂直平分线MN交x轴于点M，连接AM，求线段AM的长；
（3）若点P是直线AB上的一个动点，当△PAM的面积与长方形OACB的面积相等时，求点P的坐标．

3、如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象，由图象解答下列问题：

(1)求蜡烛在燃烧过程中高度与时间之间的函数表达式
(2)经过多少小时蜡烛燃烧完毕？
4、在平面直角坐标系xOy中，对于线段AB和点C，若△ABC是以AB为一条直角边，且满足AC>AB的直角三角形，则称点C为线段AB的“关联点”，已知点A的坐标为（0，1）．

(1)若B（2，1），则点D（3，1），E（2，0），F（0，-3），G（-1，-2）中，是AB关联点的有_______；
(2)若点B（-1，0），点P在直线y=2x-3上，且点P为线段AB的关联点，求点P的坐标；
(3)若点B（b，0）为x轴上一动点，在直线y=2x+2上存在两个AB的关联点，求b的取值范围．
5、已知一次函数y＝kx﹣4，当x＝3时，y＝﹣1，求它的解析式以及该直线与坐标轴的交点坐标．

-参考答案-
一、单选题
1、A
【解析】
【分析】
过点M作y轴的平行线，过点E、D分别作这条直线的垂线，垂足分别为F、G，求出直线AB、AC的解析式，设出点D、E、M的坐标，根据△DGM≌△MFE，建立方程求解即可．
【详解】
解：过点M作y轴的平行线，过点E、D分别作这条直线的垂线，垂足分别为F、G，
设直线AB的解析式为，把，代入得，
，解得，，
∴AB的解析式为，
同理可求直线AC的解析式为，
设点D坐标为，点M坐标为，
∵，
∴
∵，，
∴点E是由点D向右平移3个单位，向上平移9个单位得到的，则点E坐标为，
∵∠EFM=∠DGM=∠DME
∴∠FEM+∠FME=∠DMG+∠FME =90°，
∴∠FEM =∠DMG，
∵DM=EM，
∴△DGM≌△MFE，
∴DG=FM，GM=EF，
根据坐标可列方程组，b-a=3a+18+1.5b-9-1.5b+9-3a-9=b-a-3，
解得，，
所以，点M坐标为，
故选：A．

【点睛】
本题考查了求一次函数解析式和全等三角形的判定与性质，解题关键是求出直线解析式，设出点的坐标，利用全等三角形建立方程．
2、A
【解析】
【分析】
根据一次函数的性质得出y随x的增大而减小，进而求解．
【详解】
由一次函数y＝－4x＋b可知，k=－4＜0，y随x的增大而减小，
∵－3＜2，
∴y1＞y2，
故选：A．
【点睛】
本题考查一次函数的性质，熟知一次函数y＝kx＋b（k≠0），当k＜0时，y随x的增大而减小是解题的关键．
3、B
【解析】
【分析】
当不动时，距离300千米，就是A，B两地的距离；甲匀速运动，走完全程用时5小时，乙走完全程用时3小时，确定甲，乙的函数解析式，求交点坐标；分甲出发，乙未动，距离为50千米，甲出发，乙出发，且甲在前50距离50千米，甲在后距离50千米，乙到大时距离为50千米四种情形计算即可．
【详解】
∵（0，300）表示不动时，距离300千米，就是A，B两地的距离，
∴①正确；
∵甲匀速运动，走完全程用时5小时，乙走完全程用时3小时，
∴乙车比甲车晚出发1小时，却早到1小时；
∴②正确；
设，
∴300=5m，
解得m=60，
∴；
设，
∴
解得，
∴；
∴
解得t=2.5，
∴2.5-1=1.5，
∴乙车出发后1.5小时追上甲车；
∴③错误；
当乙未出发时，，
解得t=；
当乙出发，且在甲后面时，，
解得t=；
当乙出发，且在甲前面时，，
解得t=；
当乙到大目的地，甲自己行走时，，
解得t=；
∴④错误；
故选B．
【点睛】
本题考查了函数的图像，一次函数的解析式确定，交点的意义，熟练掌握待定系数法，准确捕获图像信息是解题的关键．
4、A
【解析】
【分析】
由知直线必过，据此求解可得．
【详解】
解：，
当时，，
则直线必过，
如图满足条件的大致图象是：

故选：A．
【点睛】
本题主要考查一次函数的图象，解题的关键是掌握一次函数的图象性质：①当，时，图象过一、二、三象限；②当，时，图象过一、三、四象限；③当，时，图象过一、二、四象限；④当，时，图象过二、三、四象限．
5、A
【解析】
【分析】
根据一次函数的性质，y随x增大而减小判断即可．
【详解】
解：知点，在一次函数的图像上，
∵-2<0，
∴y随x增大而减小，
∵，
∴，
故选：A．
【点睛】
本题考查了一次函数的增减性，解题关键是明确一次函数y随x增大而减小的性质．
6、D
【解析】
【分析】
根据题意和一次函数的性质，可以解答本题．
【详解】
解：∵一次函数y=kx+b（k，b为常数，且k≠0）的图象经过点（0，-1），且y的值随x值的增大而增大，
∴b=-1，k＞0，
故选：D．
【点睛】
本题考查了待定系数法求一次函数的解析式，一次函数的性质，解答本题的关键是明确题意，利用一次函数的性质解答．
7、B
【解析】
【分析】
根据直线y＝kx＋b经过一、二、四象限，可得k＜0，b＞0，从而得到直线y＝bx﹣k过一、二、三象限，即可求解．
【详解】
解：∵直线y＝kx＋b经过一、二、四象限，
∴k＜0，b＞0，
∴﹣k＞0，
∴直线y＝bx﹣k过一、二、三象限，
∴选项B中图象符合题意．
故选：B
【点睛】
本题主要考查了一次函数的图象和性质，熟练掌握一次函数的图象和性质是解题的关键．
8、A
【解析】
【分析】
先求出正比例函数解析式根据正比例函数的图象性质，当k＜0时，函数随x的增大而减小，可得y1与y2的大小．
【详解】
解：∵正比例函数的图像经过点（2，4）、代入解析式得
解得
∴正比例函数为
∵＜0，
∴y随x的增大而减小，
由于-1＜1，故y1 故选：A．
【点睛】
本题考查了正比例函数图象上点的坐标特征，用到的知识点为：正比例函数的图象，当k＜0时，y随x的增大而减小是解题关键．
9、C
【解析】
【分析】
一次函数过第一、二、三象限，则，根据图象结合性质可得答案.
【详解】
解：如图，函数的图象经过第一、二、三象限，

则函数的图象与轴交于正半轴，

故选C
【点睛】
本题考查的是一次函数的图象与性质，掌握“一次函数过第一、二、三象限，则”是解本题的关键.
10、A
【解析】
【分析】
y＞0即是图象在x轴上方，找出这部分图象上点对应的横坐标范围即可．
【详解】
解：∵一次函数y=f（x）的图象经过点（2，0），
∴如果y＞0，则x＜2，
故选：A．
【点睛】
本题考查一次函数的图象，数形结合是解题的关键．
二、填空题
1、一次函数
【解析】
略
2、
【解析】
【分析】
由两条直线的交点坐标P（1，n），先求出n，再求出方程组的解即可．
【详解】
解：∵y＝﹣x＋4经过P（1，n），
∴n=-1+4=3，
∴n=3，
∴直线l1：y＝kx＋b与直线l2：y＝﹣x＋4相交于点P（1，3），
∴，
故答案为．
【点睛】
本题考查了一次函数的交点与方程组的解的关系、待定系数法等知识，解题的关键是理解方程组的解就是两个函数图象的交点坐标．
3、（12，0）或（－，0）
【解析】
【分析】
由一次函数解析式求出点A、B的坐标，进而求得OA、OB、AB，分点C在x轴正半轴和在x轴负半轴，利用折叠性质和勾股定理求解OC即可．
【详解】
解：当x=0时，y=4，当y=0时，x=－3，
∴A(－3，0)，B（0，4），
∴OA=3，OB=4，
∴，
设点A的对应点为A1，OC=x，
当点C在x轴正半轴时，如图，
根据轴对称性质得：BA1=AB=5，OA1=5+4=9，CA1=AC=3+x，
在Rt△A1OC中，由勾股定理得：，
解得：x=12，即OC=12，
∴点C坐标为（12，0）；

当点C在x轴负半轴时，如图，
根据折叠性质得：BA1=AB=5，OA1=5－4=1，CA1=AC=3－x，
在Rt△A1OC中，由勾股定理得：，
解得：，即OC= ，
∴点C的坐标为（－，0），

综上，点C的坐标为（12，0）或（－，0），
故答案为：（12，0）或（－，0）．
【点睛】
本题考查一次函数与坐标轴的交点问题、折叠性质、勾股定理、坐标与图形，熟练掌握轴对称性质，利用分类讨论思想解决问题是解答的关键．
4、k＜1
【解析】
【分析】
利用一次函数图象与系数的关系列出关于m的不等式k-1＜0，然后解不等式即可．
【详解】
解：∵一次函数y=（k-1）x+3中，y随x的增大而减小，
∴k-1＜0，
解得k＜1；
故答案为：k＜1．
【点睛】
本题主要考查一次函数图象与系数的关系．解答本题注意理解：k＞0时，直线必经过一、三象限，y随x的增大而增大；k＜0时，直线必经过二、四象限，y随x的增大而减小．
5、＞
【解析】
【分析】
由M（1，a）和N（2，b）是一次函数y=-x+1图象上的两点，利用一次函数图象上点的坐标特征可求出a，b的值，比较后即可得出结论．
【详解】
解：当x=1时，a=-1+1=0；
当x=2时，b=-2+1=-1．
∵0＞-1，
∴a＞b．
故答案为：＞．
【点睛】
本题考查了一次函数图象上点的坐标特征，牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键．
三、解答题
1、 (1)普通板栗的单价为55元，精品板栗的单价为80元；
(2)普通板栗加工1000件，精品板栗加工3000件，所获总利润最多，最多总利润是75000元．
【解析】
【分析】
（1）设普通板栗的单价为x元，精品板栗的单价为y元，根据表格列出二元一次方程组，求解即可得；
（2）加工普通板栗a件，则加工精品板栗(4000-a)件，根据题意可得利润的函数关系式，根据一次函数的性质及自变量的取值范围可得当时，所获总利润w最多，代入求解即可得．
(1)
解：设普通板栗的单价为x元，精品板栗的单价为y元，由题意得：
，
解得x=55y=80，
答：普通板栗的单价为55元，精品板栗的单价为80元；
(2)
解：加工普通板栗a件，则加工精品板栗(4000-a)件，
由题意得：，
∵，1000≤a≤3000，
∴当时，所获总利润w最多，
w=-5×1000+80000=75000，
∴，
答：普通板栗加工1000件，精品板栗加工3000件，所获总利润最多，最多总利润是75000元．
【点睛】
题目主要考查二元一次方程组的应用及一次函数的最大利润问题，理解题意，列出方程及函数解析式是解题关键．
2、（1）；（2）5；（3）点P的坐标为（，－）或（－，）
【解析】
【分析】
（1）由坐标系中点的意义结合图形可得出A、B点的坐标，设出对角线AB所在直线的函数关系式，由待定系数法即可求得结论；
（2）由勾股定理求出AB的长，再结合线段垂直平分线的性质，可得AM＝BM，OM＝OB−BM，再次利用勾股定理得出AM的长；
（3）（方法一）先求出直线AM的解析式，设出P点坐标，由点到直线的距离求出AM边上的高h，再结合三角形面积公式与长方形面积公式即可求出P点坐标；
（方法二）由△PAM的面积与长方形OACB的面积相等可得出S△PAM的值，设点P的坐标为（x，−x＋4），分点P在AM的右侧及左侧两种情况，找出关于x的一元一次方程，解之即可得出点P的坐标，此题得解．
【详解】
解：（1）∵四边形AOBC为长方形，且点C的坐标是（8，4），
∴AO＝CB＝4，OB＝AC＝8，
∴A点坐标为（0，4），B点坐标为（8，0）．
设对角线AB所在直线的函数关系式为y＝kx＋b，
则有，解得：，
∴对角线AB所在直线的函数关系式为y＝－x＋4．
（2）∵∠AOB＝90°，
∴勾股定理得：AB＝＝4，
∵MN垂直平分AB，
∴BN＝AN＝AB＝2．
∵MN为线段AB的垂直平分线，
∴AM＝BM
设AM＝a，则BM＝a，OM＝8－a，
由勾股定理得，a2＝42＋（8－a）2，
解得a＝5，即AM＝5．
（3）（方法一）∵OM＝3，
∴点M坐标为（3，0）．
又∵点A坐标为（0，4），
∴直线AM的解析式为y＝－x＋4．
∵点P在直线AB：y＝－x＋4上，
∴设P点坐标为（m，－m＋4），
点P到直线AM：x＋y－4＝0的距离h＝＝．
△PAM的面积S△PAM＝AM•h＝|m|＝SOABC＝AO•OB＝32，
解得m＝± ，
故点P的坐标为（，－）或（－，）．

（方法二）∵S长方形OACB＝8×4＝32，
∴S△PAM＝32．
设点P的坐标为（x，－x＋4）．
当点P在AM右侧时，S△PAM＝MB•（yA－yP）＝×5×（4＋x－4）＝32，
解得：x＝，
∴点P的坐标为（，－）；
当点P在AM左侧时，S△PAM＝S△PMB－S△ABM＝MB•yP－10＝×5（－x＋4）－10＝32，
解得：x＝－，
∴点P的坐标为（－，）．
综上所述，点P的坐标为（，－）或（－，）．
【点睛】
本题考查了坐标系中点的意、勾股定理、点到直线的距离、三角形和长方形的面积公式，解题的关键：（1）根据坐标系中点的意义，找到A、B点的坐标；（2）由线段垂直平分线的性质和勾股定理找出BM的长度；（3）（方法一）结合点到直线的距离、三角形和长方形的面积公式找到关于m的一元一次方程；（方法二）利用分割图形求面积法找出关于x的一元一次方程．本题属于中等题，难度不大，运算量不小，这里尤其要注意点P有两个．
3、 (1)y=-8x+15（0≤x≤）
(2)小时
【解析】
【分析】
（1）由图象可知一次函数过（0，15），（1，7）两点，可根据待定系数法列方程，求函数关系式．
（2）将y=0的值代入，求x的解，即为蜡烛全部燃烧完所用的时间；
(1)
由图象可知过（0，15），（1，7）两点，
设一次函数表达式为y=kx+b，
∴，
解得，
∴此一次函数表达式为：y=-8x+15（0≤x≤）．
(2)
令y=0
∴-8x+15=0
解得：x＝，
答：经过小时蜡烛燃烧完毕．
【点睛】
本题考查了用待定系数法求一次函数关系式，并会用一次函数研究实际问题，具备在直角坐标系中的读图能力．
4、 (1)点E，点F；
(2)（）或（）；
(3)b的取值范围1＜b＜2或2＜b＜3．
【解析】
【分析】
（1）根据以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，△ABE为直角三角形，且AE大于AB；以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，BF大于AB即可；
（2）根据点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，得出△AOB为等腰直角三角形，可得∠ABO=∠BAO=45°，以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，利用待定系数法求出AS解析式为，联立方程组，以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，∠OBR=90°-∠ABO=45°，可得△OBR为等腰直角三角形，OR=OB=1，点R（0，-1），利用平移的性质可求BR解析式为，联立方程组，解方程组即可；
（3）过点A与AB垂直的直线交直线y=2x+2于U，把△AOB绕点A顺时针旋转90°，得△AO′U，AO′=AO=1，O′U=OB=b，根据点U（-1，b-1）在直线上，得出方程，求出b的值，当过点A的直线与直线平行时没有 “关联点”，OB=OW=b=2，得出在1＜b＜2时，直线上存在两个AB的“关联点”，当b＞2时，根据旋转性质将△AOB绕点A逆时针旋转90°得到△AO′U，得出AO′=AO=1，O′U=OB=b，根据点U（1,1+b）在直线上，列方程，得出即可．
(1)
解：点D与AB纵坐标相同，在直线AB上，不能构成直角三角形，
以点B为直角顶点，点B与点E横坐标相同，点E在过点B与AB垂直的直线上，
∴△ABE为直角三角形，且AE大于AB；

以点A为直角顶点，点A与点F横坐标相同，△AFB为直角三角形，AF=4＞AB=2，

∴点E与点F是AB关联点，
点G不在A、B两点垂直的直线上，故不能构成直角三角形，
故答案为点E，点F；
(2)
解：∵点A（0，1）点B（-1，0），OA=OB，∠AOB=90°，
∴△AOB为等腰直角三角形，AB=
∴∠ABO=∠BAO=45°，
以点A为直角顶点，过点A，与AB垂直的直线交x轴于S，
∴∠OAS=90°-∠BAO=45°，
∴△AOS为等腰直角三角形，
∴OS=OA=1，点S（1,0），
设AS解析式为代入坐标得：
，
解得，
AS解析式为，
∴，
解得，
点P（），
AP=，AP＞AB
以点B为直角顶点，过点B，与AB垂直的直线交y轴于R，
∴∠OBR=90°-∠ABO=45°，
∴△OBR为等腰直角三角形，
∴OR=OB=1，点R（0，-1），
过点R与AS平行的直线为AS直线向下平移2个单位，
则BR解析式为，
∴，
解得，
点P1（），
AP1=＞，
∴点P为线段AB的关联点，点P的坐标为（）或（）；

(3)
解：过点A与AB垂直的直线交直线y=2x+2于U，
把△AOB绕点A顺时针旋转90°，得△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（-1，b-1）在直线上，
∴
∴，
∴当b＞1时存在两个“关联点”，
当b＜1时，UA＜AB，不满足定义，没有两个“关联点”

当过点A的直线与直线平行时没有 “关联点”
与x轴交点X（-1，0），与y轴交点W（0，2）
∵OA=OX=1,∠XOW=∠AOB=90°，AB⊥XW，
∴△OXW顺时针旋转90°，得到△OAB，
∴OB=OW=2，
∴在1＜b＜2时，直线上存在两个AB的“关联点”，

当b＞2时，将△AOB绕点A逆时针旋转90°得到△AO′U，
∴AO′=AO=1，O′U=OB=b，
点U（1,1+b）在直线上，
∴
∴解得
∴当2＜b＜3时, 直线上存在两个AB的“关联点”，
当b＞3时，UA＜AB，不满足定义，没有两个“关联点”

综合得，b的取值范围1＜b＜2或2＜b＜3．
【点睛】
本题考查新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，掌握新定义线段的意义，直角三角形性质，仔细阅读新定义，由两个条件，（1）组成直角三角形，（2）AC＞AB，等腰直角三角形，勾股定理两点距离公式，待定系数法求直线解析式，图形旋转，两函数交点联立方程组，是解题关键．
5、一次函数的解析式为y＝x−4，与x轴交点的坐标是（4，0），与y轴的交点坐标是（0，−4）．
【解析】
【分析】
把x、y的值代入y＝kx−4，通过解方程求出k的值得到一次函数的解析式，根据直线与x轴相交时，函数的y值为0，与y轴相交时，函数的x值为0求出该直线与坐标轴的交点坐标．
【详解】
解：∵一次函数y＝kx−4，当x＝3时，y＝−1，
∴−1＝3k−4，解得k＝1，
∴一次函数的解析式为y＝x−4，
∵当y＝0时，x＝4，
当x＝0时，y＝−4，
∴该直线与x轴交点的坐标是（4，0），与y轴的交点坐标是（0，−4）．
【点睛】
本题考查了待定系数法求一次函数的解析式，一次函数与坐标轴的交点．正确求出直线的解析式是解题的关键．