






初中数学人教版七年级下册8.4 三元一次方程组的解法图文ppt课件
展开1.解二元一次方程组有哪几种方法?
2.解二元一次方程组的基本思路是什么?
将二元一次方程组通过“代入”或“加减”进行消元成一元一次方程.
代入消元法和加减消元法.
回顾二元一次方程组的解法
小明手头有 12 张面额分别为 1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的 4 倍. 求1元、2元、5元纸币各多少张?
思考:(1)该题中有几个等量关系?分别是什么? (2)如果设1元、2元、5元的纸币分别为x张、y张、 z张,那么可列出怎样的方程组?
设1元、2元和5元的纸币分别为 x 张、y 张和 z 张.则可列出方程组:
含有三个未知数,每个方程中含未知数的项的次数都是 1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
再求解出二元一次方程组,将 y 的值代入③中可得 z 的值.
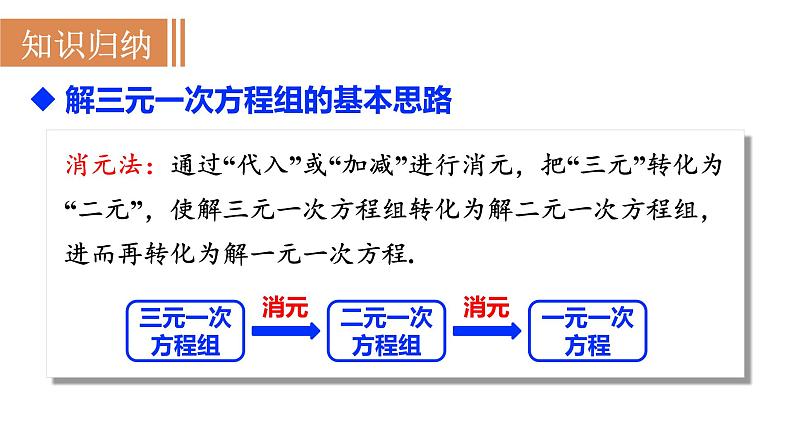
解三元一次方程组的基本思路
消元法:通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程.
思考:对于这个方程组,消哪个元比较方便?为什么?
思路:方程①只含 x、z,因此,可以由②③消去 y,得到 的方程可与①组成一个二元一次方程组.
把 x=5,z=-2代入②,得
2×5+3y-2=9,
例3 在等式y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60,求a,b,c的值.
方法一:解:根据题意,得三元一次方程组
②-①,得 a+b=1; ④
③-①,得 4a+b=10; ⑤
答:a = 3,b = -2,c = -5.
可将②-①×4,得6b-3c = 3,即2b-c = 1 ④再将 ③-①×25,得30b-24c = 60,即5b-4c = 10 ⑤
思考1:可以消去a吗?如何操作?
可将①×2+②,得6a+3c = 3,即2a+c = 1 ④再将 ①×5+③,得30a+6c = 60,即5a+c = 10 ⑤
思考2:可以消去b吗?如何操作?
解:设该校队胜 x 场、平 y 场、负 z 场. 根据题意,得 解得答:该校队胜6场,平2场,负3场.
解:②×2+③得 x+2y=53. ④
④+①得 x = 22.
解:①+②得 5x+2y=16. ④
②+③得 3x+4y=18. ⑤
⑤-④×2得 x=2.
把 x=2, y=3代入③得 z=1.
解:①-②,得2x+y=4. ④ ①+③,得x+y=3. ⑤ ④与⑤组成方程组, 得 解得 将x=1,y=2代入②, 得1+2+z=10,解得z=7.
解:②-①,得z-y=-4. ④ ③+④,得2z=-4. 解得z=-2. 将z=-2分别代入②和③,得 x=1,y=2, ∴这个方程组的解为
解:设甲、乙、丙三数分别为x、y、z,
∴甲数是10,乙数是15,丙数是10.
4.现有一种饮料,它有大、中、小3种包装,其中1个中瓶比2个小瓶便宜2角,1个大瓶比1个中瓶加1个小瓶贵4角,大、中、小各买1瓶,需9元6角,三种包装的饮料每瓶各多少元?
解:设大、中、小包装的饮料每瓶分别为x元、y元、z元,
答:大、中、小包装的饮料每瓶分别为5元、3元、1.6元,
数学七年级下册第八章 二元一次方程组8.4 三元一次方程组的解法精品ppt课件: 这是一份数学七年级下册<a href="/sx/tb_c42008_t3/?tag_id=26" target="_blank">第八章 二元一次方程组8.4 三元一次方程组的解法精品ppt课件</a>,共20页。PPT课件主要包含了学习目标,情境引入,互动新授,所以这个方程组的解为,“三元”,“二元”,二元一次方程组,一元一次方程,总结归纳,典例精析等内容,欢迎下载使用。
数学七年级下册第八章 二元一次方程组8.4 三元一次方程组的解法课文ppt课件: 这是一份数学七年级下册第八章 二元一次方程组8.4 三元一次方程组的解法课文ppt课件,共22页。PPT课件主要包含了情境导入,等量关系,用方程表示等量关系,x+y+z12,x+2y+5z22,x4y,自主探究,二元一次方程,三元一次方程,解这个方程组得等内容,欢迎下载使用。
人教版七年级下册8.4 三元一次方程组的解法教学ppt课件: 这是一份人教版七年级下册8.4 三元一次方程组的解法教学ppt课件,共11页。PPT课件主要包含了学习目标,重难点,情景导入,教学过程,探究新知,例题精讲等内容,欢迎下载使用。













