




北师大版八年级下册1 等腰三角形公开课ppt课件
展开1.通过进一步研究等腰三角形中的相等线段,深化对等腰三角形的认识.2.研究掌握特殊的等腰三角形-等边三角形的性质.3.通过在本节课中的探索证明,进一步培养学生的几何直观与推理能力,提高有条理地思考与表达水平.
有两条边相等的三角形叫做等腰三角形
小明想制作一个三角形的相框,他有四根木条长度分别为10cm,10cm,10cm,6cm,你能帮他设计出几种形状的三角形?
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.
在等腰三角形中作出一些线段,比如两底角的平分线,两腰上的中线,或两腰上的高,它们有何数量上的关系?你能证明吗?
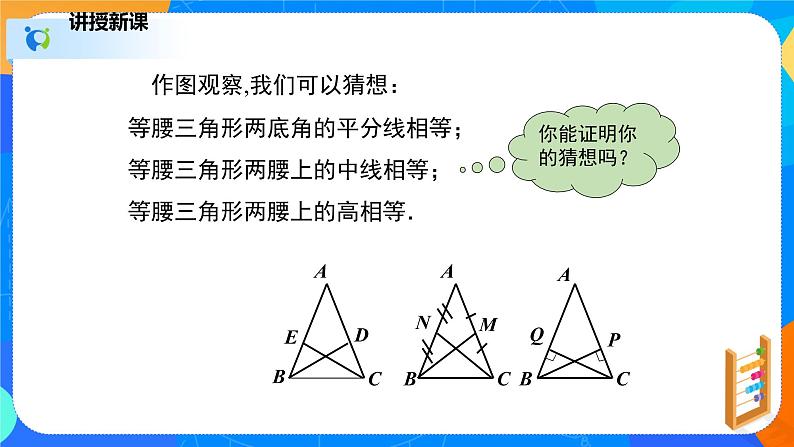
作图观察,我们可以猜想:等腰三角形两底角的平分线相等;等腰三角形两腰上的中线相等;等腰三角形两腰上的高相等.
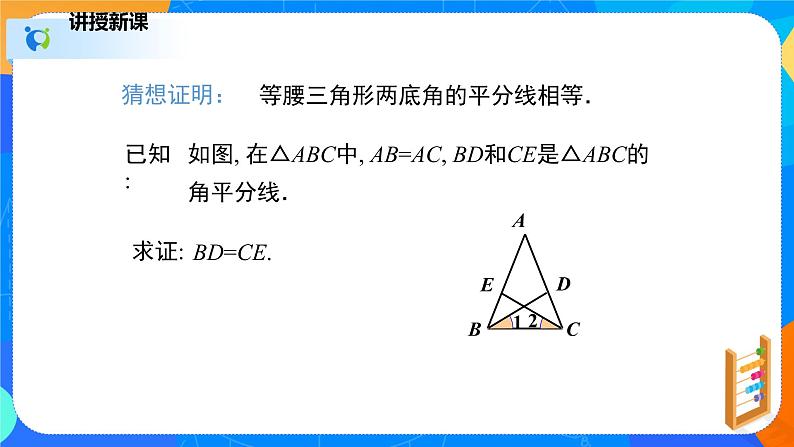
如图, 在△ABC中, AB=AC, BD和CE是△ABC的角平分线.
∠2= ∠ACB(已知),
∵AB=AC(已知),∴∠ABC=∠ACB(等边对等角).
又∵∠1= ∠ABC,
∴∠1=∠2(等式性质).
在△BDC与△CEB中,
∠DCB=∠ EBC(已知),
BC=CB(公共边),
∠1=∠2(已证),
△BDC≌△CEB(ASA).
BD=CE(全等三角形的对应边相等).
在△ABC中,如果AB=AC,∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE.
简述为:过底边的端点且与底边夹角相等的两线段相等.
如图, 在△ABC中, AB=AC,BM,CN是△ABC两腰上的中线.
又∵CM= ,BN= ,
∵AB=AC(已知),∴∠ABC=∠ACB.
∴CM=BN.在△BMC与△CNB中,
∵ BC=CB,∠MCB=∠NBC, CM=BN,
∴△BMC≌△CNB(SAS).
如图, 在△ABC中, AB=AC,BP,CQ是△ABC两腰上的高.
在△BMC与△CNB中,
∵ BC=CB,∠QBC=∠PCB, ∠BQC=∠CPB,
∴△BQC≌△CPB(AAS).
在△ABC中,如果AB=AC,AD= AC,AE= AB,那么BD=CE.
简述为:两腰上距顶点等距的两点与底边顶点的连线段相等.
如果把等腰三角形的性质用于等边三角形,你能得到什么结论?
等边三角形的三条边都相等,是一种特殊的等腰三角形.所以等边三角形具有等腰三角形的所有性质.
等边三角形是轴对称图形吗?若是,有几条对称轴呢?
等边三角形是轴对称图形,有三条对称轴.
等边三角形的内角都相等吗?为什么?
等边三角形的三个内角都相等,且都是60°.
证明:在△ABC中,∵AB=AC(已知),∴∠B=∠C(等边对等角).同理∠A=∠B.又∵∠A+∠B+∠C=180°(三角形的内角和等于180°),∴∠A=∠B=∠C=60°.
几何语言:如图,在△ABC中, AB=BC=AC, ∠A=∠B=∠C=60°.
(1)等边三角形是特殊的等腰三角形,它具有等腰三角形的所有性质.(2)等边三角形每条边上的中线、高和所对角的平分线相互重合,即“三线合一”;每条边上的中线和高的长度相等,且所在的直线都是等边三角形的对称轴.
1.如图,已知AD,BE分别是△ABC的中线和高,且AB=AC,∠EBC=20°,则∠BAD的度数为 ( )A.18° B.20° C.22.5° D.25°
2.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )
A.25° B.60° C.85° D.95°
3.下列说法:(1)等腰三角形的高、中线、角平分线互相重合;(2)等腰三角形的两腰上的中线长相等;(3)等腰三角形的腰一定大于其腰上的高;(4)等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.其中不正确的个数是( )A.1B.2C.3D.4
4.在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=( )
A.16° B.28°C.44° D.45°
5.若等腰三角形两腰上的高相交所成的钝角为100°,则顶角的度数为 ( )
A.50° B.80 ° C.100 ° D.130 °
6 .在△ABC中,AB=AC,BD、CE分别为∠ABC、∠ACB的平分线,BD=5,则CE= .
7 .如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE=______.
8. 若如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,AB,ED相交于点F,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确的有___________.(填序号)
9.如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC.
证明:∵AB=AC,∴∠ABC=∠ACB. 又∵CD⊥AB于点D,BE⊥AC于点E,∴∠AEB=∠ADC=90°, ∴∠ABE=∠ACD, ∴∠ABC-∠ABE=∠ACB-∠ACD, 即∠EBC=∠DCB.
在△BEC与△CDB中,∴△BEC≌△CDB,∴BD=CE, ∴AB-BD=AC-CE,即AD=AE, ∴∠ADE=∠AED. 又∵∠A是△ADE和△ABC的顶角,∴∠ADE=∠ABC, ∴DE∥BC.
10.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
∵ △ABC是等边三角形,
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30°.
∴ ∠BDE=(180 °-∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
11. 如图,在△ABC中,AB=AC,中线BD,CE相交于点O.求证:OB=OC.
证明:∵BD,CE是△ABC的两条中线,∴CD= AC,BE= AB,∵AB=AC,∴CD=BE,∠EBC=∠DCB.在△EBC和△DCB中,BE=CD,∠EBC=∠DCB,BC=CB,∴△EBC≌△DCB(SAS),∴∠ECB=∠DBC,∴OB=OC.
12. 如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E.求证:DE=DF.
证明:∵AB=AC,∴∠B=∠C,∵DF⊥AB,DE⊥AC,∴∠BFD=∠CED=90°,在△BDF和△CDE中,BD=DC, ∠B=∠C, ∠BFD=∠CED,∴△BDF≌△CDE(AAS),∴DE=DF.
13. 如图, △ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E,A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.
证明:AE∥BC,理由如下:∵△ABC和△DEC是等边三角形,∴BC=AC,CD=CE,∠BCA=∠ECD=60°,∠B=60°,∴∠BCA-∠DCA=∠ECD-∠DCA,即∠BCD=∠ACE,
在△ACE和△BCD中,∴△ACE≌△BCD(SAS),∴∠EAC=∠B=60°,∵∠ACB=60°,∴∠EAC=∠ACB,∴AE∥BC.
14.如图,在等边△ABC中,点D,E分别在边BC,AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.(1)求证:△ABE≌△CAD.
证明:∵△ABC为等边三角形,∴AB=AC,∠BAC=∠ACB=60°,在△BAE和△ACD中,∴△BAE≌△ACD(SAS).
(2)求∠PBQ的度数.
解:∵△BAE≌△ACD,∴∠ABE=∠CAD, ∵∠BPQ为△ABP的外角, ∴∠BPQ=∠ABE+∠BAD, ∴∠BPQ=∠CAD+∠BAD=∠BAC=60°,∵BQ⊥AD,∴∠PBQ=30°.
等边三角形的三个内角都相等,并且每个角都等于60°
等腰三角形重要线段的性质
底角的两条角平分线相等
北师大版八年级下册1 等腰三角形教学课件ppt: 这是一份北师大版八年级下册<a href="/sx/tb_c94875_t3/?tag_id=26" target="_blank">1 等腰三角形教学课件ppt</a>,共28页。PPT课件主要包含了复习导入,探索新知,归纳总结,思维拓展,典例精练,课堂练习,课堂小结,布置作业等内容,欢迎下载使用。
初中数学北师大版八年级下册1 等腰三角形公开课ppt课件: 这是一份初中数学北师大版八年级下册1 等腰三角形公开课ppt课件
北师大版第一章 三角形的证明1 等腰三角形课文内容ppt课件: 这是一份北师大版第一章 三角形的证明1 等腰三角形课文内容ppt课件,共22页。PPT课件主要包含了学习目标,情境导入,方法一,方法二,探索交流,等边对等角,等角对等边,归纳总结,例题解析,再由AC⊥BD等内容,欢迎下载使用。












