北师大版八年级下册1 等腰三角形教学课件ppt

这是一份北师大版八年级下册1 等腰三角形教学课件ppt，文件包含北师大版数学八年级下册11等腰三角形第1课时同步课件pptx、北师大版数学八年级下册11等腰三角形第1课时教学设计含教学反思docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

应用作为证明基础的公理证明等腰三角形的性质定理。掌握推理证明的基本要求，明确条件和结论。
能够借助数学符号语言利用综合证明法证明等腰三角形的性质定理。熟练证明的基本步骤和书写格式。
启发引导学生体会探索结论和证明结论。
探索证明等腰三角形性质定理的思路与方法，掌握证明的基本要求和方法。
掌握推理证明的基本要求，明确条件与结论，能否用数学语言正确表达。
前面我们学习判定三角形全等的方法有哪些？
三边对应相等的两个三角形全等.
两边及其夹角对应相等的两个三角形全等.
两角及其夹边对应相等的两个三角形全等.
你能用有关的基本事实和已经学习过的定理证明 “两角及其中一角的对边对应相等的两个三角形全等 （AAS）”这个结论吗？
条件：两角及其中一角的对边对应相等结论：两个三角形全等
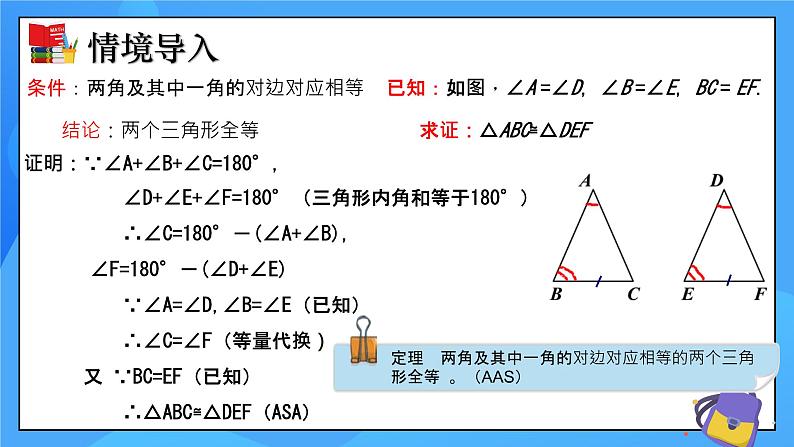
条件：两角及其中一角的对边对应相等 已知：如图，∠A =∠D，∠B =∠E，BC = EF.
结论：两个三角形全等 求证：△ABC≌△DEF
证明：∵∠A+∠B+∠C=180°， ∠D+∠E+∠F=180°（三角形内角和等于180°） ∴∠C=180°－(∠A+∠B)， ∠F=180°－(∠D+∠E) ∵∠A=∠D,∠B=∠E（已知） ∴∠C=∠F（等量代换） 又 ∵BC=EF（已知） ∴△ABC≌△DEF（ASA）
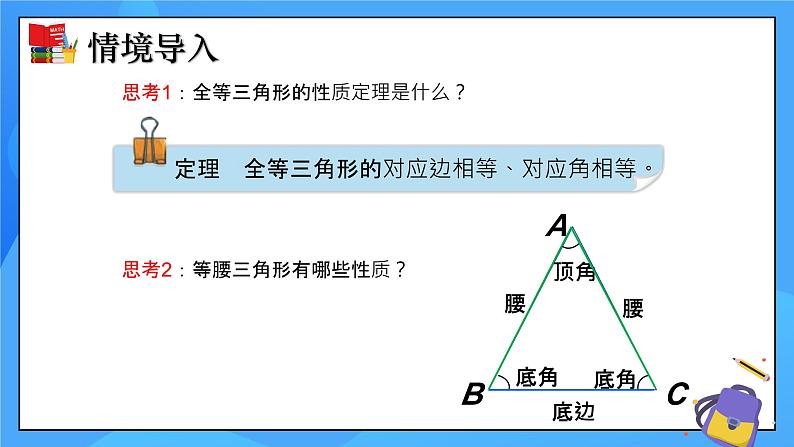
思考1：全等三角形的性质定理是什么？
思考2：等腰三角形有哪些性质？
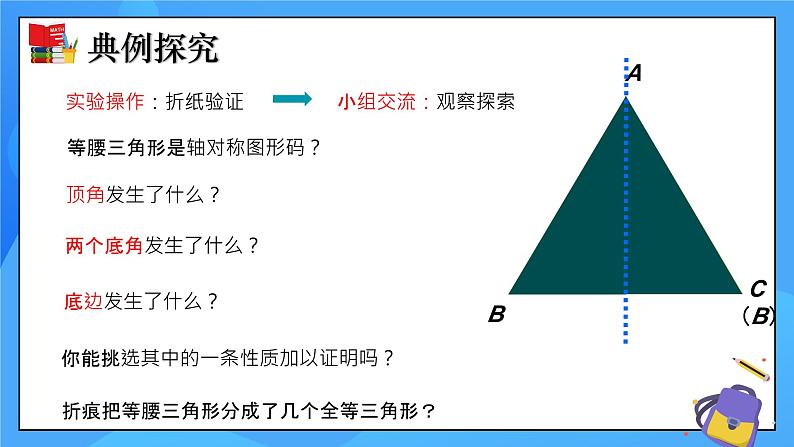
你能挑选其中的一条性质加以证明吗？
折痕把等腰三角形分成了几个全等三角形？
等腰三角形是轴对称图形码？
条件：等腰三角形 已知：如图，在△ABC 中，AB = AC.
结论：两底角相等 求证：∠B =∠C
证明：取 BC 的中点 D，连接 AD. 在△ABD 和△ACD 中， ∵ AB = AC，BD = CD，AD = AD， ∴ △ABD ≌ △ACD（SSS）. ∴ ∠B =∠C （全等三角形的对应角相等）.
分析：我们曾经利用折叠的方法说明了这两个底角相等﹒实际上，折痕将等腰三角形分成了两个全等三角形．这启发我们，可以作一条辅助线，把原三角形分成两个全等的三角形，从而证明这两个底角相等.这里我们不妨取BC的中点。
∵AB ＝ AC（已知）
∴∠B ＝∠C（等边对等角）
思考：线段AD还具有怎样的性质（回顾折纸活动）
1.线段AD把顶角平分。 （上述定理的证明方法还可以是作辅助线顶角平分线AD）
2.线段AD与底边垂直。
∵AB ＝ AC， ∠1 ＝∠2（已知）∴BD ＝ DC， AD⊥BC（等腰三角形三线合一）
1. 等腰三角形的顶角的平分线，既是底边上的中线，又是底边上的高。
2. 等腰三角形的底边上的中线，既是顶角的平分线，又是底边上的高。
∵AB ＝ AC， BD ＝ DC（已知）∴∠1 ＝∠2， AD⊥BC（等腰三角形三线合一）
3. 等腰三角形的底边上的高，既是顶角的平分线，又是底边上的中线。
∵AB ＝ AC，AD⊥BC（已知）∴∠1 ＝∠2， BD ＝ DC（等腰三角形三线合一）
1.在△ABC 中，AB = AC.（1）若∠A = 40°，则∠C 等于多少度？（2）若∠B = 72°，则∠A 等于多少度？
2. 已知：如图，点 B，E，C，F 在同一条直线上，AB = DE，AC = DF，BE = CF. 求证：∠A =∠D.
证明： ∵BE＝ CF， ∴BE + CE＝ CF + EC， ∴BC = EF. 又∵AB = DE AC = DF， ∴△ABC ≌△DEF（SSS）. ∴∠A =∠D.（全等三角形的对应角相等）
1.如图,在△ABD中,C是BD上的一点，且AC⊥BD，AC=BC=CD，（1）求证： △ABD是等腰三角形;（2）求∠BAD的度数.
教材“习题1.1”中第1、3题.